Косоугольные проекции

Рассмотрим косоугольную проекцию на плоскость XOY, при которой орт переходит в вектор , т. е. направление проекции задается вектором . Такое преобразование в пространстве однородных координат можно задать с помощью матрицы

.

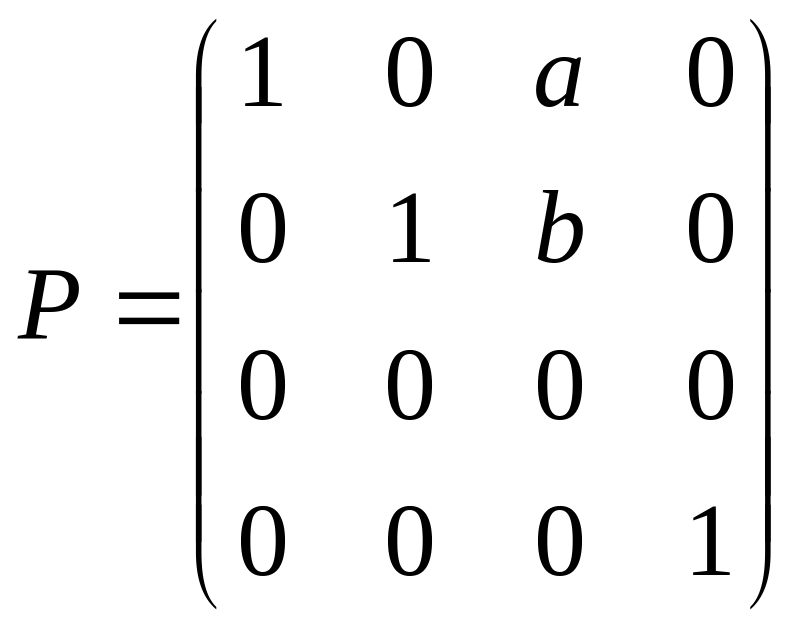В проекции кавалье вектор переходит в вектор , а в кабинетной проекции — в вектор , причем в обеих проекциях .

Центральные проекции

П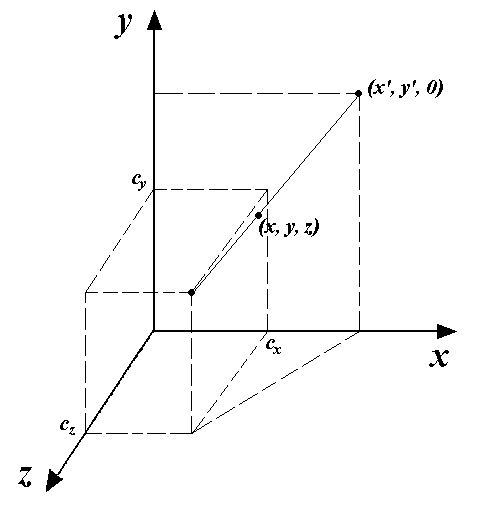 редположим, что центр проектирования находится в точке , а картинная плоскость совпадает с плоскостью XOY. Возьмем произвольную точку изображаемого объекта и определим ее проекцию на выбранную плоскость (рис. 7.7). Прямую, проходящую через точки и зададим в параметрическом виде:

(7.1).

Т

Рис. 7.7. Центральная проекция

на плоскость XOY

еперь найдем точку пересечения этой прямой с картинной плоскостью. Она определяется из условия равенства нулю третьей координаты:

,

откуда определяем значение параметра t, при котором точка прямой принадлежит координатной плоскости:

.

Подставляя это значение в формулу (7.1), мы получим координаты проекции точки :

Рис. 12

(7.2)

Фактором, влияющим на перспективное изменение размеров, является деление наличие координаты z в знаменателе. Чем ближе оказывается точка к центру проекции, тем больше знаменатель, а соответственно, и координаты точки.

Мы будем рассматривать ситуацию, когда центр проекции лежит на оси OZ, а сама ось направлена от наблюдателя к проекционной плоскости, т. е. . Тогда формулы (7.2) приобретают вид

(7.3)

В однородных координатах такое преобразование можно записать с помощью двух операций. Сначала умножаем матрицу проективного преобразования на исходную точку и получаем точку в четырехмерном пространстве:

. (7.4)

Затем проецируем эту точку в пространство однородных координат путем деления на четвертую компоненту:

.

Посмотрим теперь, что происходит с пучком параллельных прямых под действием матрицы проектирования. Пусть задан пучок прямых, параллельных вектору . Тогда параметрическое уравнение прямой, принадлежащей этому пучку, имеет вид

.

Из формулы (7.4) следует, что в результате проектирования получим множество точек

.

Переходя к однородным координатам и умножив числитель и знаменатель каждой дроби на , получим точки вида

.

Теперь в каждой компоненте вектора числитель и знаменатель поделим на :

.

Переходя к пределу при , получим точку

Таким образом, получаем, что после проектирования пучок параллельных прямых пересекается в точке схода . Понятно, что у каждого пучка своя точка схода. Если пучок прямых параллелен плоскости XOY, т. е. , то точка схода оказывается на бесконечности, а значит, прямые остаются параллельными.

Для построения перспективной проекции с несколькими точками схода используется матрица перспективного преобразования без проектирования

.

Теперь точки пространства сначала подвергаются перспективному преобразованию, а затем осуществляется проекция.

Определим точки схода для прямых, параллельных осям координат. Для прямых результатом проективного преобразования будет множество точек , где . При получим точку с координатами . При проекции на плоскость XOY получим точку . Пучок прямых перейдет в , , а точкой схода для него будет , которая при проектировании перейдет в точку, лежащую на оси OX . Аналогично для пучка прямых, параллельных оси OY получим точку схода на оси OY . Эти три точки на плоскости являются главными точками схода.