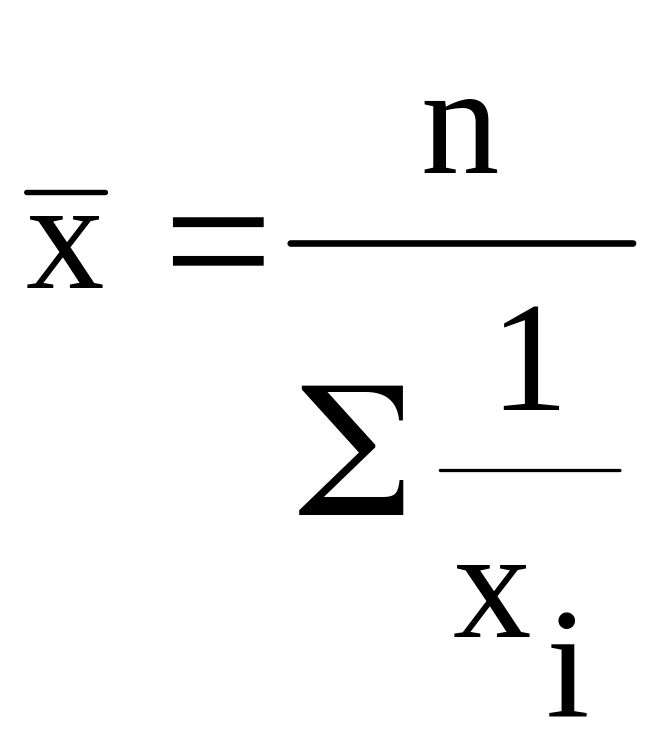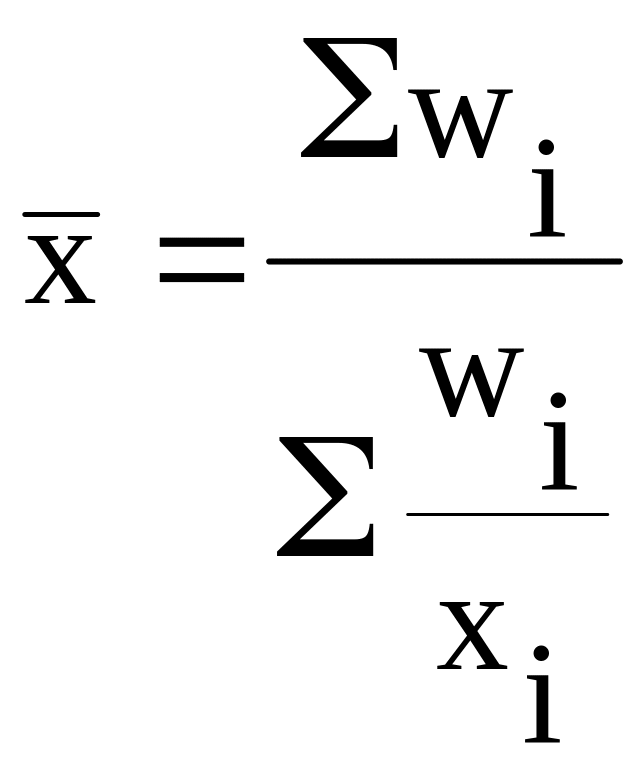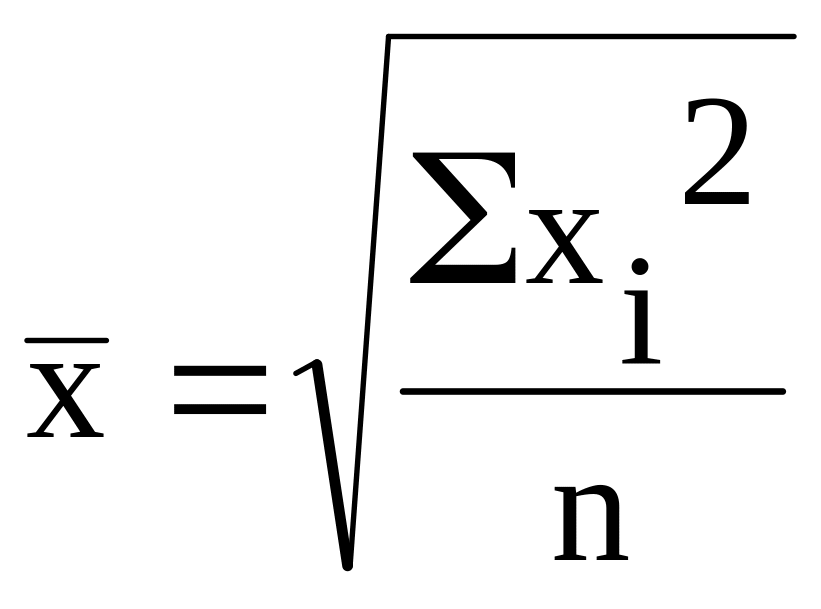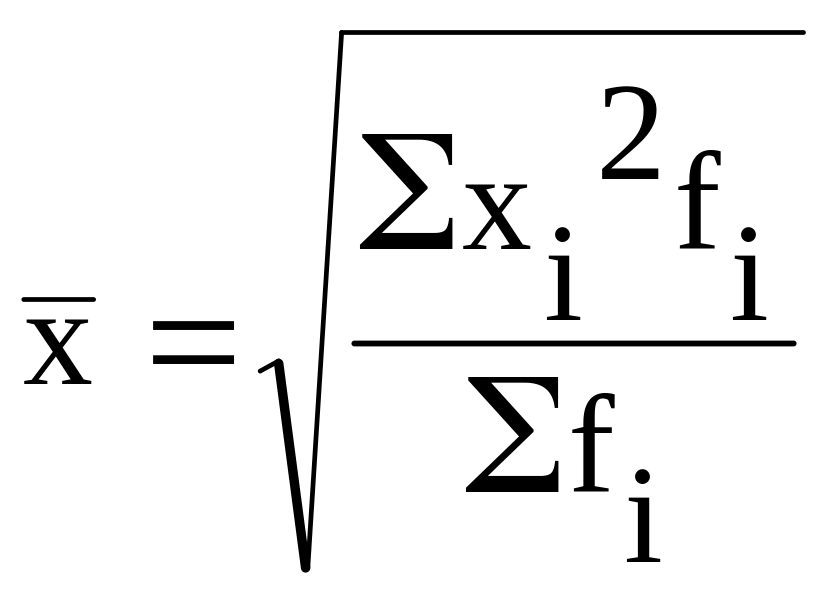Тема 3. Средние величины и показатели вариации

Средние величины - это величины, которые позволяют охарактеризовать явление по количественно варьирующему признаку.

Для осреднения различных признаков используются разные виды средних величин. Выбор вида средней осуществляется индивидуально в каждом случае и зависит от наличия исходных данных и вида признака.

Каждый вид средней, кроме того, имеет две формы: простую и взвешенную. Простая средняя используется в тех случаях, когда каждое значение признака встречается только один раз. Если некоторые значения признака повторяются неоднократно, т.е. данные сгруппированы, для расчета средней используются взвешенные формы средних. В табл. 3.1 приводятся формулы основных видов средних величин в двух формах.

Основные обозначения:

- среднее значение признака;

х_i - индивидуальные значения осредняемого признака;

n - количество единиц совокупности;

f_i - частота (вес) индивидуальных значений осредняемого признака;

w_i = x_if_i - произведение индивидуального значения признака и его частоты.

Таблица 3.1

Виды и формы средних величин

	Формы		Простая	№ фор-мулы	Взвешенная	№ фор-мулы
Виды
1			2	3	4	5
1. Арифме­тическая				(3.1)		(3.2)
2. Гармони­ческая				(3.3)		(3.4)
3. Квадра­тическая				(3.5)		(3.6)
4. Геомет­рическая				(3.7)		(3.8)
5. Хроноло­гическая				(3.9)

Чаще всего в расчетах используется простая или взвешенная арифметическая средняя.

В том случае, когда нет данных о частотах отдельных признаков, но имеются сведения о произведении индивидуального значения признака на его частоту, среднюю арифметическую можно заменить средней гармонической. При этом гармоническая простая используется только тогда, когда равны объемы совокупностей.

Средняя квадратическая, простая и взвешенная, используется, как правило, для расчета средних отклонений.

Геометрическая средняя используется для осреднения таких признаков, для которых характерна мультипликативная зависимость. Чаще всего геометрическая средняя используется для расчета средних темпов роста и средних индексов.

Хронологическая средняя применяется для расчетов средних уровней в моментных рядах динамики.

Помимо средних величин, в статистическом анализе используются и структурные средние: мода и медиана.

Мода - это значение признака, которое чаще всего встречается в ряде распределения.

В дискретных рядах модой является значение признака в той группе, у которой наблюдается наибольшая частота. Определить моду в этом случае можно визуально.

В интервальных рядах распределения мода также находится в той группе, у которой наибольшая частота. Но так как в интервальных рядах признак может принимать любое значение в заданном интервале, точное значение моды следует определять по специальной формуле:

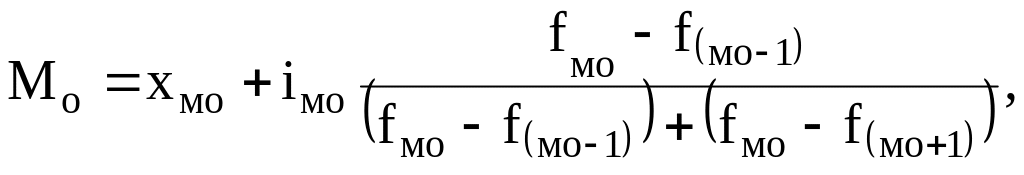(3.10)

где х_мо - нижняя граница модального интервала;

i _мо - величина модального интервала;

f _мо - частота модального интервала;

f _(мо-1) - частота интервала, предшествующего модальному;

f _(мо+1) - частота интервала, следующего за модальным.

Модальным является интервал, имеющий наибольшую частоту

Значение моды, рассчитанное по формуле (3.10), не может быть меньшим, чем нижняя граница модального интервала, и не будет превышать верхнюю границу модального интервала.

Медиана - это значение признака, стоящего в центре ранжированного ряда распределения.

В дискретном ряде распределения медиана равна значению признака в той группе, у которой сумма накопленных частот равна или превышает половину суммы всех частот ряда распределения.

Сумма накопленных частот находится последовательным сложением частот каждой группы. Так, для первой группы сумма накопленных частот будет равна частоте этой группы, для второй группы - сумме частот первой и второй группы, для третьей группы - сумме частот первой, второй и третьей группы и т.д. накопленная частота последней группы будет равна общей сумме частот ряда распределения.

В интервальном ряде распределения медиана находится по специальной формуле:

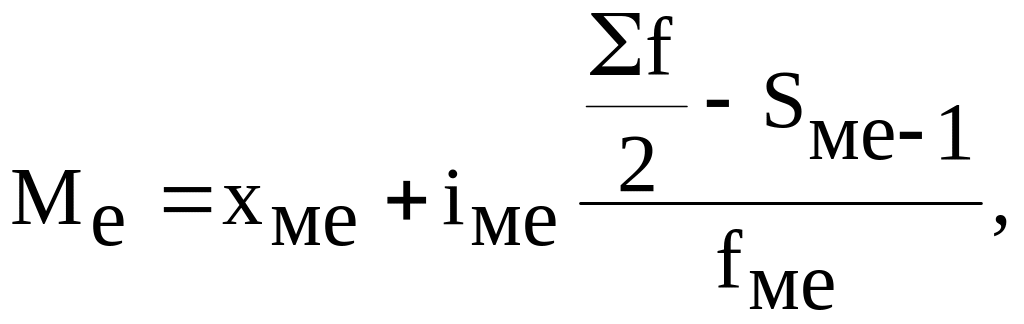(3.11)

где х_ме - нижняя граница медианного интервала;

I _ме - величина медианного интервала;

f _ме - частота медианного интервала;

Σf - сумма всех частот ряда распределения;

S _ме-1 - сумма частот, накопленных до медианного интервала.

Медианным считается интервал, сумма накопленных частот которого равна или превышает половину всех частот ряда распределения

Значение медианы будет не меньше, чем значение нижней границы медианного интервала, и не превысит значения верхней границы медианного интервала.

По соотношению моды, медианы и средней можно судить о характере распределения признака. Распределение может быть симметричным. В этом случае наблюдается равенство между модой, медианой и средним значением признака (рис. 3.1).

частота признака, (fi)	у
		значение признака (хi)			х

Рис. 3.1. Симметричный ряд распределения

В реальной жизни симметричное распределение встречается нечасто, поэтому чаще следует определять характер асимметрии. Если между модой, медианой и средней выполняется соотношение (3.12), то мы имеем дело с правосторонней асимметрией.

М_о < М_е < . (3.12)

частота признака, (fi)	у
		значение признака (хi)			х

Рис. 3.2. Ряд распределения с правосторонней асимметрией

При наличии левосторонней асимметрии мода, медиана и средняя связаны следующим образом:

М_о > М_е > . (3.13)

частота признака, (fi)	у
		значение признака (хi)			х

Рис. 3.3. Ряд распределения с левосторонней асимметрией

Определить наличие асимметрии можно и с помощью относительного показателя - коэффициента асимметрии. Он может быть рассчитан в двух вариантах - на основе моды или медианы.

, (3.14)

. (3.15)

Если A_s > 0, имеется правосторонняя асимметрия, если A_s < 0 - левосторонняя.

Показатели вариации характеризуют степень отклонения реальных значений признака от среднего значения и друг от друга. Они делятся на три группы: абсолютные, средние и показатели относительного рассеивания.

К абсолютным показателям вариации относится размах вариации, который характеризует отклонение крайних значений признака.

(3.16)

где x_max, x_min - максимальное и минимальное значение признака в изучаемой совокупности.

К средним показателям вариации относятся среднее линейное отклонение, среднее квадратическое отклонение и дисперсия. Эти показатели существуют в двух формах: простой и взвешенной.

Простая форма применяется для несгруппированных данных, взвешенная - если данные сгруппированы. Форма расчета средних показателей вариации совпадает с формой расчета средней величины.

Среднее линейное отклонение находится как отношение суммы отклонений индивидуальных значений признаков от средней (взятой по модулю) к количеству единиц совокупности (формулы (3.17) и (3.18). Среднее линейное отклонение показывает, на сколько единиц в среднем индивидуальные значения признака отклоняются от его среднего значения.

, (3.17)

. (3.18)

Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько единиц в среднем индивидуальные значения признака отклоняются от средней, но сумма отклонений возводится в квадрат. Рассчитывается также в простой и взвешенной форме.

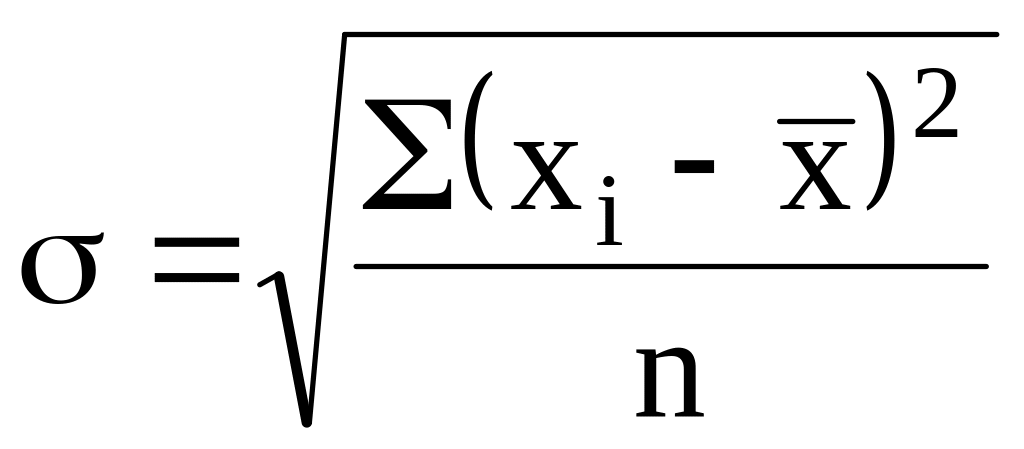, (3.19)

. (3.20)

Дисперсия представляет собой сумму квадратов отклонений индивидуальных значений признака от средней. Данный показатель не имеет единиц измерения. В простой форме дисперсия имеет вид:

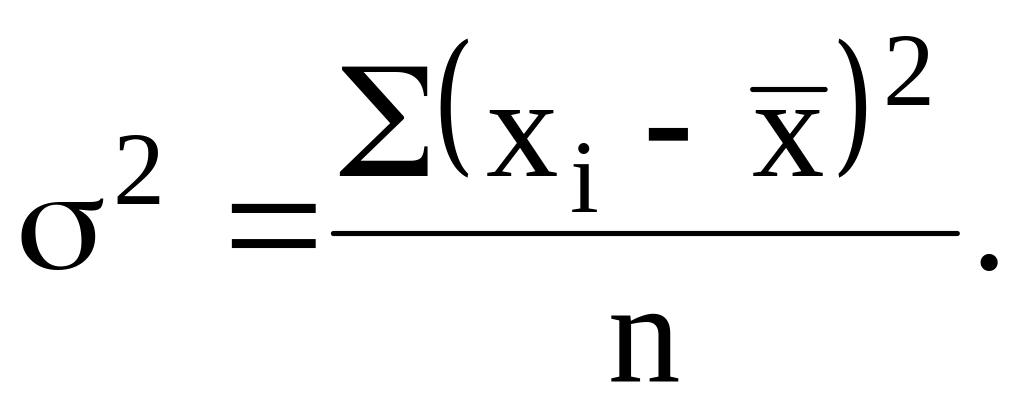(3.21)

Во взвешенной форме:

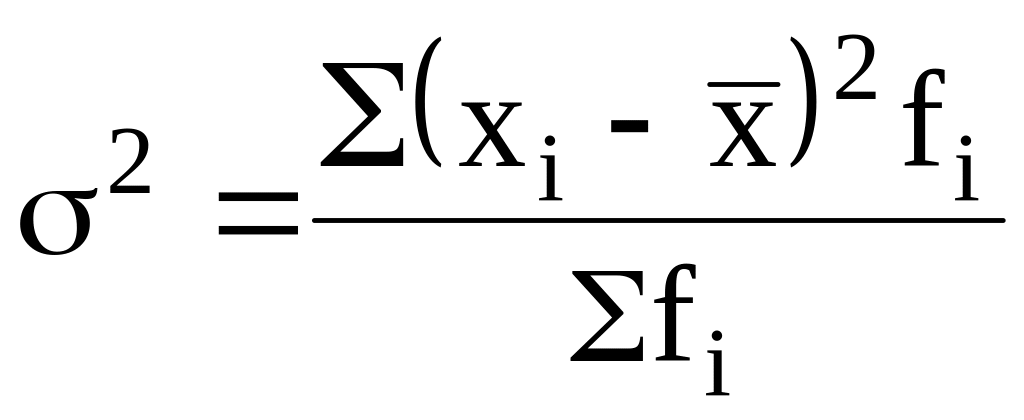. (3.22)

Можно рассчитать дисперсию по методу моментов. В этом случае расчет производится по формуле:

(3.23)

Дисперсия делится на общую, внутригрупповую и межгрупповую.

Общая дисперсия характеризует вариацию, обусловленную воздействием всех признаков. Она рассчитывается по формулам (3.21), (3.22), (3.23).

Внутригрупповая дисперсия измеряет вариацию, возникающую внутри группы. Она рассчитывается по формуле:

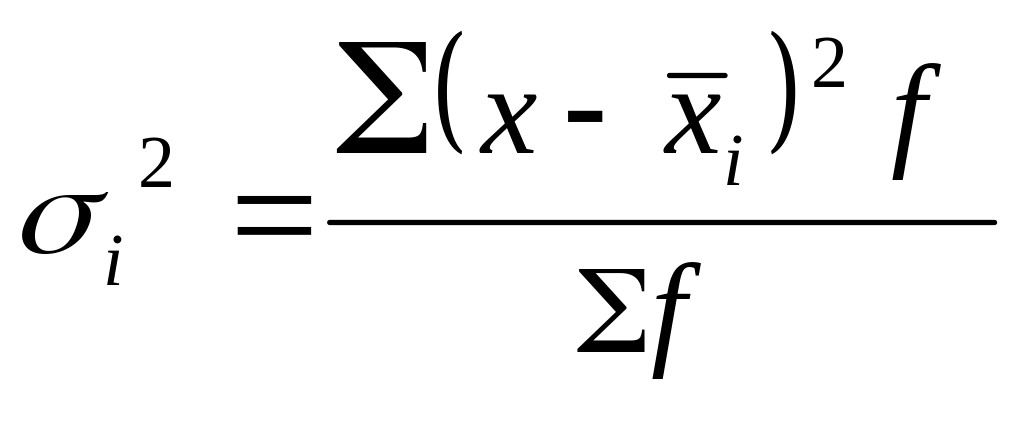. (3.24)

где - групповая средняя.

В расчетах часто используется средняя из внутригрупповых дисперсий. Она определяется следующим образом:

_. (3.25)

Где f – количество единиц в группе.

Межгрупповая дисперсия измеряет вариацию, обусловленную признаком, положенным в основание группировки. Она показывает колеблемость групповых средних вокруг общей средней и рассчитывается по формуле 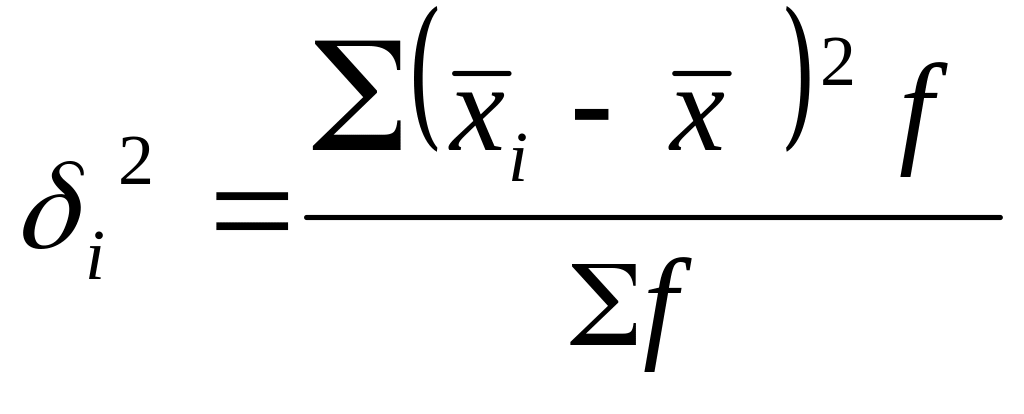(3.26).

. (3.26)

Общая дисперсия может быть найдена как сумма средней из внутригрупповых и межгрупповой дисперсии.

. (3.27)

Показатели относительного рассеивания являются мерой вариации признака и позволяют сопоставлять степень вариации у различных совокупностей. Данные показатели находятся как отношение абсолютных или средних показателей вариации к среднему значению признака.

Коэффициент осцилляции рассчитывается как отношение размаха вариации к среднему значению признака (в процентах):

(3.28)

Относительное линейное отклонение находится как частное от деления среднего линейного отклонения на среднее значение признака (в процентах):

(3.29)

Коэффициент вариации является мерой типичности средней и находится по формуле:

(3.30)

Если значение коэффициента вариации не превышает 33%, средняя считается типичной для совокупности и ее можно применять в экономических расчетах.