Задача 6.3

Для определения среднего возраста мужчин, вступающих в брак, и доли мужчин, вступающих в повторный брак, была произведена 5-% выборка, результаты которой приведены в табл. 6.1:

Табл. 6.1

Социальная группа	Число мужчин, чел. (f)	Средний возраст, лет ( )	Среднее квадратическое отклонение, лет ( )
Рабочие	60	24	5
Служащие	40	27	8

С вероятностью 0,954 определите пределы, в которых будет находиться средний возраст мужчин, вступающих в брак.

Решение. В данной задаче для определения пределов среднего возраста мужчин, вступающих в брак, необходимо найти предельную ошибку выборочной средней.

Определим, какие показатели у нас имеются в условии:

• Вес каждой группы – f – 60 и 40 человек;

• Общий объем выборки n = 100;

• коэффициент доверия t = 2;

• внутригрупповые средние - - равные 24 и 27 годам;

• внутригрупповые средние квадратические отклонения - - равные 5 и 8 годам соответственно.

Так как объем выборки не превышает 5 %, среднюю ошибку выборочной средней следует рассчитывать по формуле (6.1):

(6.1)

Но в данной задаче имеется дополнительная сложность – в условии приводится не общая дисперсия признака ( ), а средние квадратические отклонения по каждой группе ( ) . Для определения общей дисперсии следует воспользоваться правилом сложения дисперсий, изложенным в главе 3. Тогда общая дисперсия признака будет равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии.

. (3.27)

Средняя из внутригрупповых дисперсий определяется как средняя арифметическая взвешенная (формула 3.25), и для ее расчета необходимо воспользоваться данными из табл. 6.1:

Межгрупповая дисперсия рассчитывается по формуле 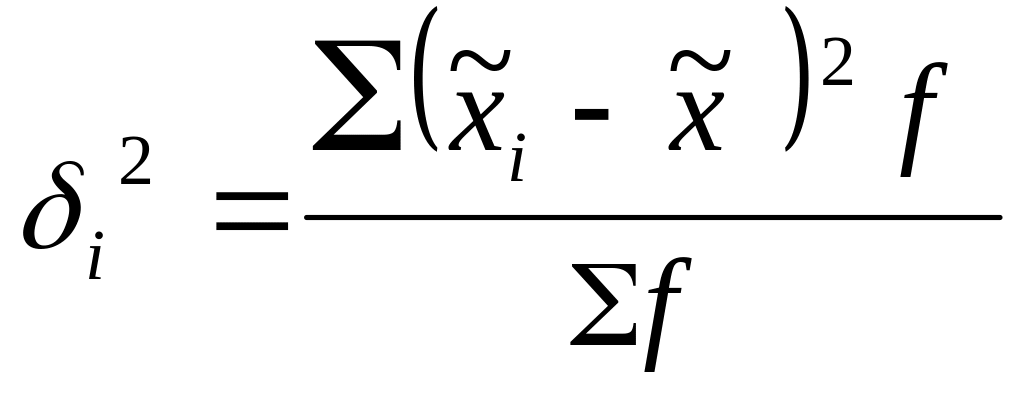(3.26):

. (3.26)

Для расчета данного показателя необходимо предварительно рассчитать средний возраст по всей совокупности как среднюю арифметическую взвешенную. Для нашего примера:

года.

Тогда межгрупповая дисперсия равна:

Общая дисперсия, рассчитанная по формуле (3.27), равна:

Тогда, средняя ошибка среднего возраста вступающих в брак, согласно формуле (6.1):

года.

Предельная ошибка в данном случае составит, согласно формуле (6.7):

года.

Пределы, в которых заключен средний возраст вступающих в брак по всей генеральной совокупности, определим, исходя из равенства (6.9):

.

Следовательно, в генеральной совокупности средний возраст вступающих в брак будет не ниже 23,9 года и не превысит 26,5 лет. Такая закономерность будет наблюдаться в 954 случаях из 1000.

Тема 7. Анализ взаимосвязей

При анализе связей между показателями особое внимание уделяется вероятностным связям. Для выявления их наличия и определения тесноты используется корреляционно-регрессионный анализ, метод параллельных рядов, графический метод, методы анализа атрибутивных и альтернативных рядов.

При проведении корреляционно-регрессионного анализа выделяют следующие этапы:

1. подбирается уравнение регрессии, и рассчитываются его параметры;

2. определяются показатели тесноты связи;

3. устанавливается сила связи;

4. оценивается надежность параметров уравнения регрессии и показателей тесноты связи.

На первом этапе выбирают уравнение регрессии. Для этого можно воспользоваться графическим методом, изобразив эмпирические значения факторного и результативного признака на оси координат.

Если наблюдается линейная связь между признаками, рекомендуется воспользоваться уравнением прямой:

(7.1)

При наличии нелинейных форм связи можно использовать следующие уравнения:

• параболы второго порядка:

, (7.2)

• параболы третьего порядка:

, (7.3)

• показательной функции:

, (7.4)

• полулогарифмической функции:

, (7.5)

где - теоретические значения результативного признака;

а₀, а₁, а₂, а₃ - параметры уравнения регрессии;

х - эмпирические (реальные) значения факторного признака.

Для расчета параметров уравнения регрессии используют метод наименьших квадратов:

(7.6)

где у - реальные значения результативного признака.

Базируясь на методе наименьших квадратов, можно составить следующие системы нормальных уравнений для расчета параметров а₀, а₁ и т.д.:

а) для уравнения прямой

(7.7)

б) для уравнения параболы второго порядка

(7.8)

в) для показательной функции

(7.9)

г) для полулогарифмической функции

(7.10)

Для определения параметров уравнений может использоваться либо способ совместного решения уравнений, либо способ определителей.

По способу определителей параметры уравнения прямой находятся следующим образом:

(7.11)

(7.12)

Параметры уравнения показательной функции:

(7.13)

(7.14)

Параметры уравнения полулогарифмической функции по методу определителей равны:

(7.15)

(7.16)

Выбор уравнения, наиболее точно описывающего связь между факторным и результативным признаками, осуществляется при помощи остаточной дисперсии (формула (7.25)). Наиболее точным считается то уравнение, у которого остаточная дисперсия имеет наименьшее значение.

Для определения тесноты связи используются различные показатели, как параметрические, так и непараметрические: коэффициент линейной корреляции, индекс корреляции (корреляционное отношение), коэффициент Фехнера, коэффициент корреляции рангов Спирмэна, коэффициенты ассоциации и контингенции, коэффициент взаимной сопряженности Чупрова и т.д.

Коэффициент корреляции используется только при линейной форме связи и рассчитывается по формулам:

(7.18)

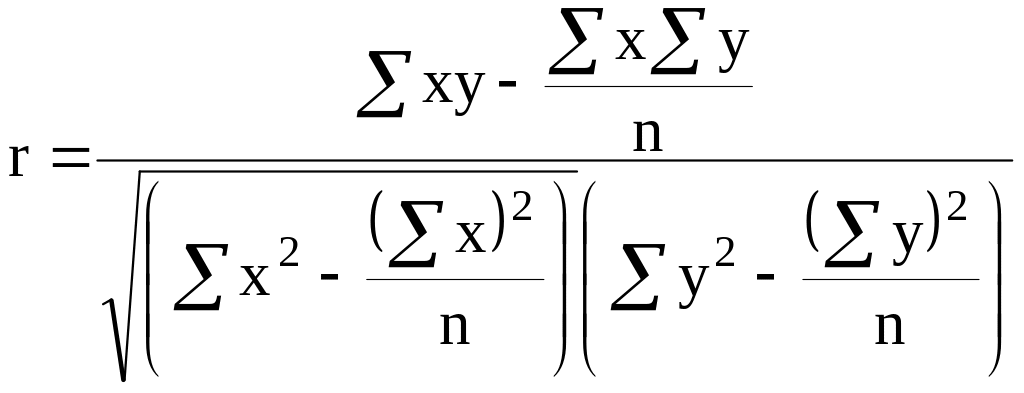. (7.19)

Индекс корреляции (корреляционное отношение) используется для линейной и нелинейной форм связи. Он находится как отношение:

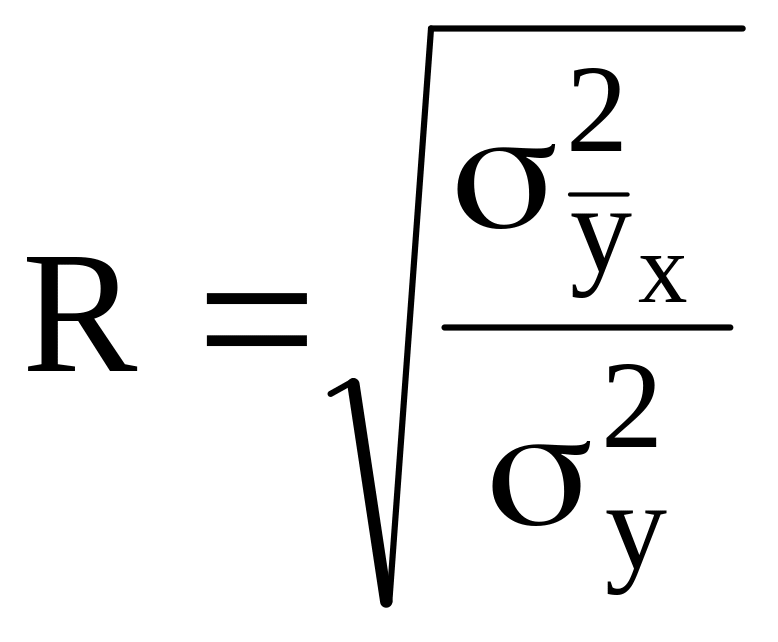, (7.20)

где - факторная дисперсия, обусловленная изменением результативного признака у только под воздействием изменения факторного признака х. Рассчитывается по формуле:

, (7.21)

- общая дисперсия результативного признака у, обусловленная воздействием всех факторов, а не только фактора х.

, (7.22)

где - теоретические значения результативного признака, рассчитанные на основе уравнения регрессии;

- среднее значение результативного признака;

n - количество единиц в совокупности;

у_i - реальные значения результативного признака.

Коэффициент линейной корреляции "r" может принимать значения от -1 до 1. Отрицательное значение свидетельствует о наличии обратной связи между признаками х и у.

Индекс корреляции принимает значения от 0 до 1.

Если показатели тесноты связи будут равны 0, значит связь между х и у отсутствует.

Сила связи находится на основании показателей тесноты связи по шкале Чеддока.

Таблица 7.1