Лабораторна робота № 5 Множинна нелінійна регресія Завдання

1. На основі статистичних даних показника і факторів та 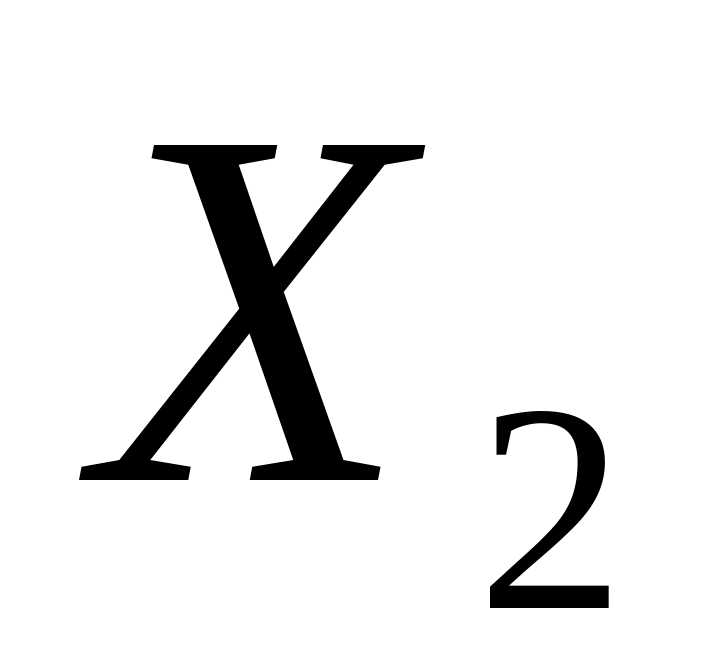знайти оцінки параметрів регресії, якщо припустити, що стохастична залежність між факторами і показником має вигляд .

2. Використовуючи критерій Фішера, оцінити з надійністю адекватність прийнятої математичної моделі статистичним даним.

3. Якщо модель адекватна, то знайти

• оцінки прогнозу та з надійністю його надійний інтервал;

• оцінки частинних коефіцієнтів еластичності для прогнозу.

Варіанти вхідних даних та відповідних економетричних моделей для лабораторної роботи №5 див. у табл. 5.

Теоретичні відомості

Найбільш досконалою і вивченою серед усіх багатовимірних регресійних моделей є лінійна. Лише деякі природні та економічні процеси можна моделювати за допомогою лінійної моделі. ЇЇ вибір залежить від процесу і тривалості спостереження за ним. Деякі процеси при нетривіальному спостереженні за ними можна з певним наближенням моделювати за допомогою лінійної багатофакторної регресії. Для повного опису процесу, як правило, необхідного використовувати нелінійні регресійні залежності.

В економіці для деяких процесів такі залежності відомі. Як приклад можна назвати виробничу функції Кобба-Дугласа.

Використання ЕОМ дає змогу по новому підійти до вивчення процесів, що залежать від багатьох факторів. Як і для парного регресійного аналізу, для багатофакторного регресійного аналізу можна розглядати два типи моделей: лінійні відносно оцінюваних параметрів та не лінійні відносно оцінюваних параметрів.

Багатофакторні регресійні моделі першого типу

, (5.1)

де можуть бути різними функціями (наприклад, , , ), замінною змінних зводяться до лінійної моделі вигляду

(5.2)

Оцінки параметрів прогнозу і надійних інтервалів знаходять спочатку для лінійної моделі, а потім переходять до нелінійної моделі.

Окремі багатофакторні, нелінійні відносно параметрів, моделі можна зводити до багатофакторних лінійних регресійних моделей. Прикладом таких багатофакторних моделей може бути модель

Регресіями такого виду можна описувати процеси, що залежать від досягнутого рівня прогресу без істотних обмежень на ці процеси. Логарифмуванням і наступною заміною змінних таку модель можна звести до лінійної.

Методичні вказівки

Для прикладу розглянемо регресію на такого вигляду:

(5.3)

1. Знаходження оцінок параметрів регресії.

Для приведення регресії (5.3) до лінійної про логарифмуємо її

(5.4)

Величини показника і факторів ( ) мають бути додатними ( ), де – число періодів, що спостерігаються.

Проведемо заміну

;

;

;

.

Для загальності запису системи нормальних рівнянь введемо позначення

.

Таким чином регресія (5.3) запишеться у вигляді

(5.5)

Для оцінки параметрів регресії (5.3) система нормальних рівнянь має вигляд

Якщо , то система (5.6) має єдиний розв’язок і його можна знайти одним з методів розв’язування системи лінійних рівнянь. (див. лаб. роб. №3, п.)

2. Адекватність моделі. Для визначення адекватності прийнятої моделі експериментальним даним використаємо критерій Фішера. Розрахункове значення статистики Фішера знаходиться за формулою

, (5.7)

де

, (5.8)

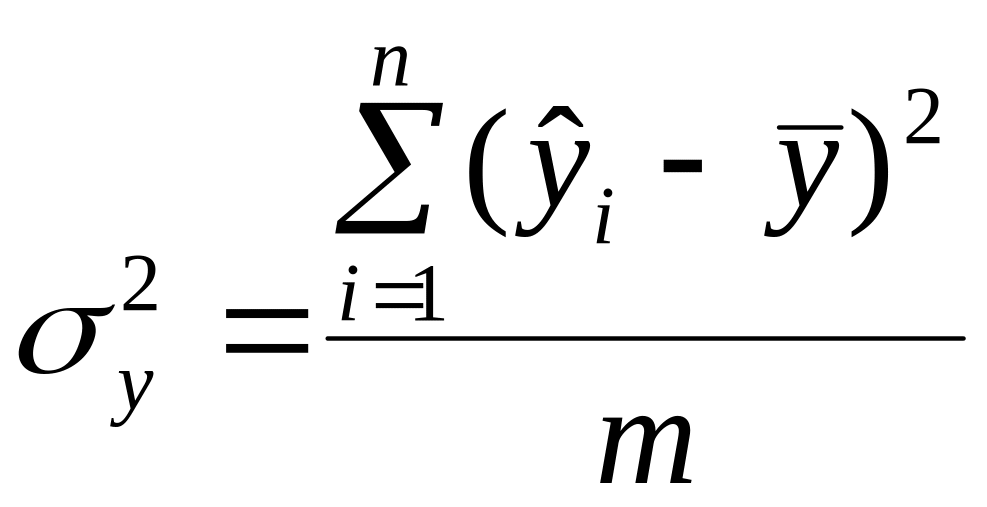(5.9)

– кількість дослідів, – кількість включених у регресію факторів, які впливають на показник та ( ) – число ступенів вільності.

Для даної ймовірності ( рівня значущості) і числа ступенів вільності , знаходиться критичне значення . Отримане розрахункове значення порівнюють з критичним.

Твердження 5.1. Якщо , то з надійністю можна вважати, що математична модель адекватна статистичним даним. Значення береться з табл.8. за відомими , та або за допомогою вбудованої функції FРАСПОБР.

3. А) Довірчий інтервал для прогнозованого значення показника . Для цього знайдемо спочатку довірчий інтервал для до лінійного виду регресії (5.3), а потім перетворимо межі довірчого інтервалу, використовуючи зворотні перетворення.

Отже довірчий інтервал для прогнозованого значення показника :

. (5.10)

де

(5.11)

(5.12)

Критичне значення критерію Стьюдента беремо з табл.7, яке залежить від параметрів та числа ступенів вільності або використовуючи функцію СТЬЮДРАСПОБР.

З формул замін виражається через наступним чином , то

(5.13)

Зокрема, та .

Б) Оцінки частинних коефіцієнтів еластичності для прогнозу

, , (5.14)

, . (5.15)