Теоретичні відомості

Явище, яке залежить від багатьох факторів, можна описати за допомогою множинної регресії. Дослідивши взаємозв’язок процесів у минулому і діставши функціональний зв’язок між ними, можна з певною вірогідністю планувати майбутнє.

Розглянемо модель множинної регресії для трьох факторів. Припустимо, що маємо пар спостережень. Висуваємо гіпотезу, що між показником та трьома факторами та існує лінійна стохастична залежність

, (4.1)

в якій – показник, та – фактори, – параметри, – випадкова величина, що є відхиленням від передбачуваної функціональної залежності.

Справжні значення параметрів знайти не можна. Позначимо через та оцінки параметрів регресії. Тоді рівняння множинної лінійної регресії

(4.2)

є оцінкою моделі (4.1).

Методичні вказівки

1. Оцінимо цю модель за допомогою метода МНК (методу найменших квадратів)

у матричній формі матиме вигляд

, (4.3)

де ­– матриця спостережуваних значень факторів , та – фіктивний фактор, всі значення якого дорівнюють одиниці, – вектор-стовпець спостережуваних значень показника, – вектор-стовпець розрахункових значень показника, – вектор-стовпець оцінюваних параметрів.

Параметри регресії шукаються за формулою

. (4.4)

2. Взаємозв’язок між окремими ознаками описується за допомогою кореляційної матриці. Кореляційна матриця

, (4.5)

де .

Безрозмірна величина називається коефіцієнтом кореляції факторів та і характеризує ступінь лінійної залежності цих факторів. Якщо , то випадкові величини та зв’язані додатною кореляцією (при зростанні однієї випадкової величини друга також має тенденцію до зростання); якщо , то випадкові величини зв’язані від’ємною кореляцією (при зростанні однієї випадкової величини друга має тенденцію до спадання)

Для будь-яких двох факторів та коефіцієнт кореляції має властивість

. (4.6)

Вибіркова кореляційна матриця володіє властивостями:

• вона симетрична відносно головної діагоналі ( ),

• елементи головної діагоналі дорівнюють одиниці ( ).

3. Перевірка на загальну мультиколінеарність за методом Фаррара-Глобера.

Твердження 4.1. Якщо , то з імовірністю можна вважати, що між факторами існує загальна мультиколінеарність.

Для відомої ймовірності і , знаходимо значення або за допомогою вбудованої функції ХИ2ОБР.

Обчислення здійснюється за формулою

, (4.7)

де , – число періодів, що спостерігаються, – число факторів включених у регресію.

4. –статистика для перевірки мультиколінеарності між та .

Для з’ясування між якими саме факторами існує мультиколінеарність використовується –статистика. Для цього спочатку обчислюють – частинні коефіцієнти кореляції за формулою

, (4.8)

де – елементи матриці .

, (4.9)

Для цих частинних коефіцієнтів кореляції використовується –статистика

. (4.10)

Значення порівнюються з критичним значенням критерію Стьюдента , яке залежить від параметрів та числа ступенів вільності .

Твердження 4.2. Якщо є деяке , то з надійністю можна стверджувати, що між факторами та існує мультиколінеарність.

5. Усунення мультиколінеарності.

Якщо між двома факторами та існує мультиколінеарність, то один з факторів виключається з розгляду.

6. Критерій Фішера ( -статистика).

Твердження 4.3. Якщо , то з надійністю можна вважати, що математична модель адекватна статистичним даним. обчислюється за формулою

, (4.11)

де – коефіцієнт детермінації, – число періодів, що спостерігаються, – число параметрів рівняння регресії.

Коефіцієнт детермінації

або

, (4.12)

Дисперсії та шукаємо за формулами:

(4.13),

, (4.14)

де , .

Значення береться з табл.8 за відомими , та .

7. А) Довірчий інтервал для параметрів регресії

, , (4.15)

де беремо з табл.7 , – діагональні елементи матриці

, (4.16)

. (4.17)

; (4.18)

(4.19)

або

або

.

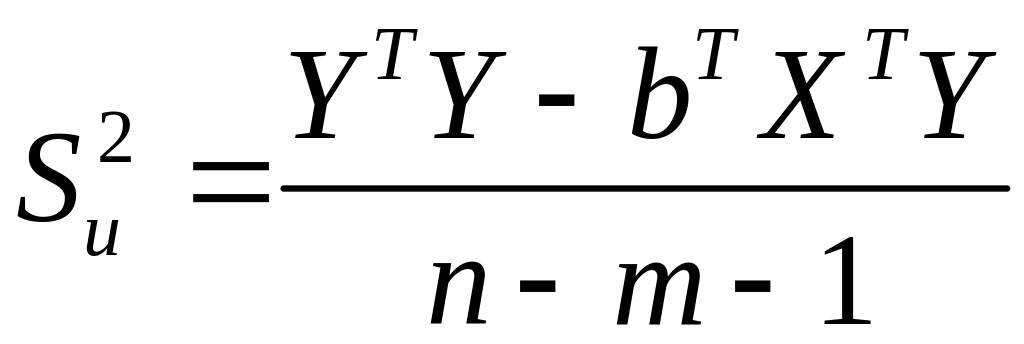Б) Довірчий інтервал для показника .

Використаємо знайдені з попереднього пункту для обчислення за формулою:

, . (4.20)

Тоді довірчий інтервал для показника має вигляд:

, . (4.21)

Зокрема, та .

В) Довірчий інтервал для прогнозованого значення показника .

Використаємо обраховані в попередньому пункті значення для , та , маємо

. (4.22)

Отже довірчий інтервал для прогнозованого значення показника :

. (4.23)

Зокрема, та .

10. Частинні коефіцієнти еластичності для прогнозу знаходимо за формулами

, , (4.24)

, . (4.25)