34. Матрица. Обратная матрица. Свойства обратной матрицы.

Числовой матрицей размером М*Н, М – строки, Н – столбцы – называют таблицу чисел.

Обратная матрица – это такая матрица 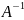, при умножении на которую исходная матрица А даёт в результате единичную матрицу Е: А = А=Е. Квадратная матрица называется невырожденной (обратной), если её определитель не равен 0.

Свойства обратной матрицы:

1. det = 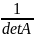, где det означает определитель.

2. = для любых двух обратимых матриц.

3. = где T обозначает транспонированную матрицу.

4. (kA) − 1 = k − 1A − 1 для любого коэффициента .

5. Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A - 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

35. Матрица. Обратная матрица. Нахождение обратной матрицы 2-го порядка.

36. Матрица. Обратная матрица. Нахождение обратной матрицы 3-го порядка.

37. Понятие неориентированного графа. Вершина. Ребро. Нулевой граф. Неполный граф. Полный граф. Примеры.

Если в графе пары не упорядочены (неизвестно какая вершина называется началом, а какая - концом), то такой граф называется неориентированным.

Элементы множества точек называются вершинами.

Элементы множества кривых, представляющих собой пару, называются рёбрами.

Граф, у которого все вершины изометричны, называется нулевым.

Граф, в котором присутствуют не все возможные графы или дуги называется неполным графом.

Если существуют все возможные дуги или рёбра, то это полный граф.

38. Понятие неориентированного графа. Полный граф. Правило подсчета ребер в полном графе.

Если в графе пары не упорядочены (неизвестно какая вершина называется началом, а какая - концом), то такой граф называется неориентированным.

Если существуют все возможные дуги или рёбра, то это полный граф.

Рёбра в полном графе считаются по формуле: n(n-1)/2, где n – это вершина.

39. Понятие неориентированного графа. Степень вершины.

Если в графе пары не упорядочены (неизвестно какая вершина называется началом, а какая - концом), то такой граф называется неориентированным.

Степенью вершины точки в неориентированном графе называют число рёбер, инцидентных (исходящих) из вершины.

Если точки являются концами ребра Х или точки являются началом или концами дуги Х, то вершины точек и ребро/дуга являются инцидентными.

40. Понятие ориентированного графа. Вершина. Дуга. Полустепень исхода (захода) вершины.

Если в графе пары упорядочены (известно какая вершина называется началом, а какая концом), то такой граф называется ориентированным.

Элементы множества точек называются вершинами.

Ориентированные рёбра – это и есть дуги.

Полустепенью исхода (захода) вершины точки ориентированного графа называют число дуг, исходящих (заходящих) в вершины точки.

41. Путь в графе. Цикл.

Путём в графе одной вершины к другой называется такая последовательность рёбер, по которой можно проложить маршрут между этими вершинами, при этом никакое ребро маршрута не должно встречаться более одного раза.

Циклом называется путь, в котором совпадают начало с концом. Если все вершины цикла разные, то такой цикл называется элементарным или простым циклом. Если же цикл включает в себя все рёбра графа по одному разу, то такой цикл называется Эйлеровой линией.

42. Связные графы.

2 вершины называются связными, если в графе существует путь с концом в этих вершинах. Связный граф называется таким, если все вершины связные.

43. Понятие графа. Деревья. Свойства деревьев.

Множество вершин и множество рёбер без повторений пар и петель называется графом.

Дерево – это любой связанный граф, не имеющий циклов.

Свойства:

1. Для каждой пары вершины дерева существует единственный путь их соединения.

2. Любое ребро к дереву является мостом.

3. Мост – ребро, если при удалении которого граф теряет связность.

44. Понятие графа. Изоморфные графы.

Множество вершин и множество рёбер без повторений пар и петель называется графом.

Изоморфные графы - это графы, у которых: одинаковое количество вершин; если вершины одного графа соединены ребром, то и соответствующие им вершины другого графа тоже соединены ребром. Изоморфные = одинаковые.

45. Матрица смежности и инцидентности графа.

Инцидентность – это понятие, используемое в отношении ребра и вершины: если В1 и В2 – вершины, а Е – соединяющее их ребро, тогда вершина В1 и ребро Е инцидентны, вершины В2 и Е тоже инцидентны. Если Х выходит из В или заходит в М, если В является концом (началом) ребра (дуги) Х, то говорят, что В и Х инцидентны.

Матрица инцидентности графа — это матрица, значения элементов которой характеризуется инцидентностью соответствующих вершин графа (по вертикали) и его рёбер (по горизонтали). Для неориентированного графа элемент принимает значение 1, если соответствующие ему вершина и ребро инцидентны. Для ориентированного графа элемент принимает значение 1, если инцидентная вершина является началом ребра, значение -1, если инцидентная вершина является концом ребра; в остальных случаях (в том числе и для петель) значению элемента присваивается 0.

Смежность — понятие, используемое в отношении только двух рёбер либо только двух вершин: Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными (ср. Инцидентность.).

Вершины В и М графа Г называются смежными, если рёбра их соединяющие принадлежат Х.

Матрица смежности графа — это матрица, значения элементов которой характеризуются смежностью вершин графа. При этом значению элемента матрицы присваивается количество рёбер, которые соединяют соответствующие вершины (то есть которые инцидентны обоим вершинам). Петля считается сразу двумя соединениями для вершины, то есть к значению элемента матрицы в таком случае следует прибавлять 2.