- •Зачем представителям юридической специальности изучать математику и информатику?
- •Понятие множества. Способы задания множества. Подмножество данного множества. Универсум. Операции над множествами (пересечение, объединение, разность).
- •Понятие множества. Диаграммы Эйлера-Венна. Дополнение.
- •Высказывание. Элементарное высказывание. Основные операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция).
- •Правильные рассуждения. Тавтология. Выполнимая формула. Тождественно ложная формула. Опровержимая формула.
- •Совершенная дизъюнктивная нормальная форма.
- •Совершенная конъюнктивная нормальная форма.
- •Тавтология. Доказательство при помощи таблицы истинности.
- •Тавтология. Доказательство при помощи рассуждения от противного.
- •Постоянные и переменные величины. Понятие функции. Область определения и область значения функции.
- •Понятие функции. Табличный способ задания функции.
- •Понятие функции. Графический способ задания функции.
- •Понятие функции. Аналитический способ задания функции.
- •Понятие функции. Элементы поведения функции. Возрастающая функция. Неубывающая функция. Примеры.
- •Понятие функции. Элементы поведения функции. Убывающая функция. Невозрастающая функция. Примеры.
- •Понятие функции. Элементы поведения функции. Ограниченная функция. Неограниченная функция. Примеры.
- •Понятие функции. Элементы поведения функции. Выпуклая вниз функция. Выпуклая вверх функция. Периодическая функция. Примеры.
- •Понятие функции. Сложная функция. Примеры.
- •Понятие функции. Линейная интерполяция.
- •Дробно-линейная функция. График.
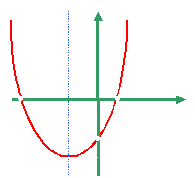
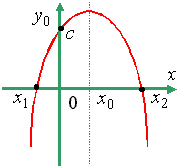
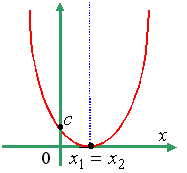
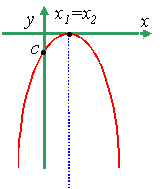
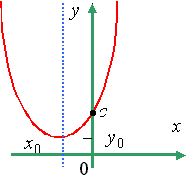
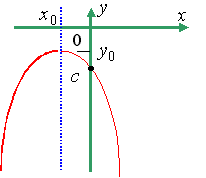
- •Квадратическая функция. График.
- •Преобразование графиков
- •Матрица. Обратная матрица. Свойства обратной матрицы.
- •Матрица. Обратная матрица. Нахождение обратной матрицы 2-го порядка.
- •Матрица. Обратная матрица. Нахождение обратной матрицы 3-го порядка.
- •Понятие неориентированного графа. Вершина. Ребро. Нулевой граф. Неполный граф. Полный граф. Примеры.
- •Информатика. Структура предметной области. Основные задачи информатики. Основные области исследований информатики.
- •Междисциплинарные направления информатики. Информатика в юриспруденции.
- •Формулировка предметной задачи. Задачная ситуация.
- •Формализация предметной задачи. Общая схема постановки и решения предметных задач.
- •Понятие о модели. Типы моделей. Представления о системном подходе. Коммуникация как передача информации о модели.
- •Информационные системы. Этапы развития информационных систем. Основные процессы в информационной системе. Свойства информационной системы.
- •Элементы комбинаторики. Генеральная совокупность без повторений. Размещения, сочетания и перестановки без повторений. Формулы расчета.
- •Элементы комбинаторики. Генеральная совокупность с повторениями. Размещения, сочетания и перестановки с повторениями. Формулы расчета.
- •Элементарное событие. Пространство элементарных исходов. Событие. Примеры. Достоверное, невозможное и случайное событие.
- •События. Действия над ними. Диаграммы Венна.
- •Вероятность. Классическая вероятность. Примеры.
- •Вероятность. Статистическая вероятность. Примеры.
- •Вероятность. Геометрическая вероятность. Примеры.
- •Совместность событий. Правило сложения вероятностей двух совместных и несовместных событий.
- •Независимость событий. Правило умножения вероятностей.
- •Формула полной вероятности.
- •Формула Байеса.
Дробно-линейная функция. График.
Функция вида
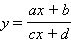 (a,
b, c, d – некоторые постоянные) называется
дробно-линейной.
(a,
b, c, d – некоторые постоянные) называется
дробно-линейной.
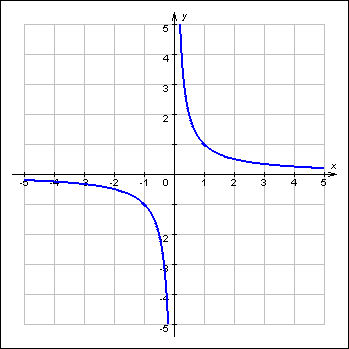
+ смотри в тетради и ищи.
Квадратическая функция. График.
Функция |
|
называется квадратичной функцией. |
|
|
|
D>0 |
|
|
D=0 |
|
|
D<0 |
|
|
+ смотри в тетради и ищи.
Преобразование графиков
Г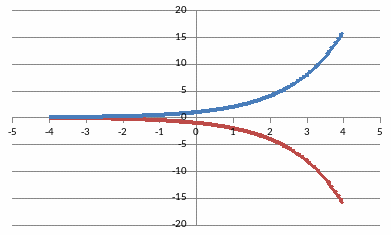 рафик
функции y
= - f(x)
получается симметричным отображением
графика y=
f(x)
относительно оси Ох.
рафик
функции y
= - f(x)
получается симметричным отображением
графика y=
f(x)
относительно оси Ох.
График функции у = f(|x|) получается из графика функции y= f(x) следующим преобразованием: при х ≥ 0 график y= f(x) сохраняется, а при х < 0 полученная часть графика отображается симметрично относительно оси Оу.
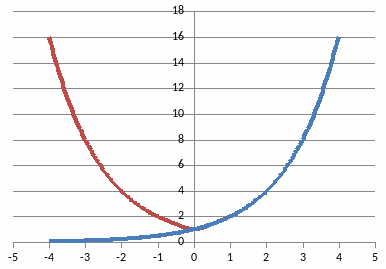
График функции у = |f(x)+а|
Происходит два преобразования графика:
Параллельный перенос вдоль оси Оу на а единиц вверх или вниз;
И
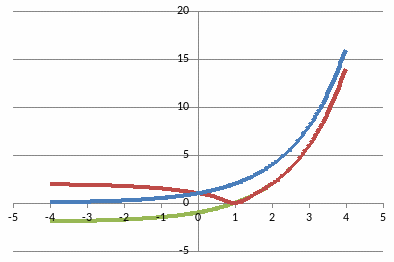 отображение относительно оси Ох.
отображение относительно оси Ох.
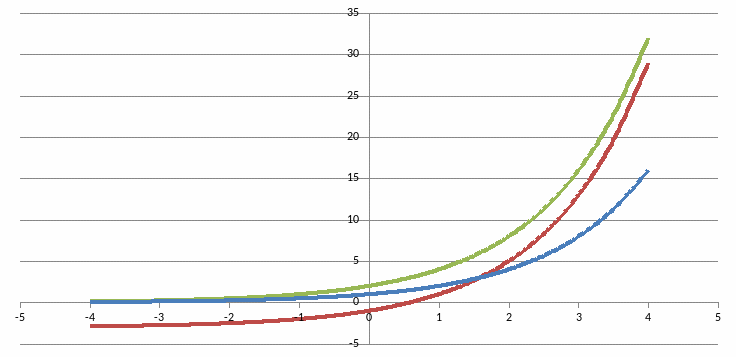
График функции y = f(x+a)+b
Происходит два преобразования графика:
Параллельный перенос вдоль оси Оу на b единиц вверх или вниз;
И параллельный перенос вдоль оси Ох на a единиц вправо или влево.
+ смотри в тетради и ищи.
Показательная функция.
Показательная
функция — математическая функция
![]() .
.
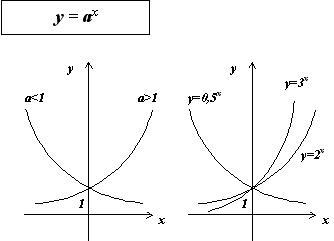
Свойства:
![]()
![]()
![]()
![]()
+ ищи.
Логарифмическая функция.
Логарифмической
функцией называется функция вида f(x) =
logax, определённая при![]() .
.
Построение графиков. График логарифмической функции logaх можно построить, воспользовавшись тем, что функция logaх обратна показательной функции y = ax. Поэтому достаточно построить график функции y = ax, а затем отобразить его симметртрично относительно прямой у = х.
+ ищи.
Взаимно обратные функции.
Пусть на множестве М задана функция и = ф(х), а на множестве значений этой функции задана функция х = г(и). Функция г называется обратной к функции ф, если для любого х из множества М выполняется равенство г(ф(х))=х.
+ ищи.
Числовая матрица. Элемент матрицы. Размерность матрицы. Квадратная матрица. Нулевая матрица. Единичная матрица.
Числовой матрицей размером МН, М – строки, Н – столбцы, называют таблицу чисел.
Элемент матрицы - ?
Размерность матрицы - ?
Квадратная матрица – это матрица, у которой число строк М = числу столбцов Н.
Нулевая матрица – матрица, состоящая из одних нулей.
Единичная матрица – это квадратная матрица.
+ смотри в тетради.
Числовая матрица. Сложение и вычитание матриц.
Числовой матрицей размером МН, М – строки, Н – столбцы, называют таблицу чисел.
Сложение. Применимо только к матрицам одинакового размера.
Вычитание. Применимо только к матрицам одного размера.
+ смотри в тетради.
Числовая матрица. Умножение матриц. Транспонирование матриц.
Числовой матрицей размером МН, М – строки, Н – столбцы, называют таблицу чисел.
Умножение на число. Каждый элемент матрицы умножается на число.
Транспонирование - ?
Умножение матриц. Есть Ц=(Циж) – элемент который есть сумма Аиж * Биж, то есть для получаемой Циж нужно и-строка А и ж – строка Б.
+ смотри в тетради.
Матрица. Определители 2-го порядка.
Определитель – это число, которое для квадратной матрицы считается по некоторым правилам. Порядок определителя – определитель матрицы.
+ смотри в тетради.
Матрица. Определители 3-го порядка.
Определитель – это число, которое для квадратной матрицы считается по некоторым правилам. Порядок определителя – определитель матрицы. В каждом произведении неи чисел из одного 1 столбца или одной строки. Произведение чисел из 1 диагонали берётся со знаком +, а из другой со знаком -.
+ смотри в тетради.
Матрица. Алгебраическое дополнение. Минор.
Минором (Миж) А называется определитель матрицы получаемый из А вычёркиванием и и ж.
+ ищи и смотри в тетради.
Матрица. Разложение определителя по строке или столбцу.
Определитель н-ного пор… можно вычислить через определитель н-1 порядка по формулам: (смотри в тетради).
Разложение определителя по и-той строке. Каждый элемент и-той строки умножается на своё дополнение и полученное определение суммируется.
Разложение множителя по ж-тому столбцу - ?
+ иищи и смотри в тетради.
Матрица. Свойства определителей.
Числовой матрицей размером М*Н, М – строки, Н – столбцы – называют таблицу чисел.
Свойства определителей:
Определитель транспонированной матрицы = определителю исходной матрицы (пример в тетради).
Если поменять местами 2 столбца и 2 строки определителя, то определитель изменит свой знак (+/-).
Если определитель содержит 2 строки и 2 столбца одинаковых, то …
Если определитель содержит 0 строк или 0 столбцов, то он = 0.
Общий множитель в стоках или столбцах можно вынести за знак определителя.
Определитель не изменится, если к любой строке добавить или вычесть любую другую строку умноженное на любое число.