33.Таблица интегралов

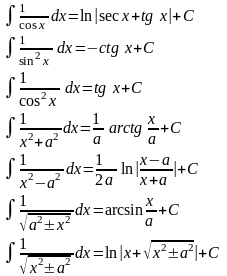
34. Методы вычисления неопределенного интеграла (непосредственное интегрирование, подстановкой, по частям).

Почленное интегрирование (метод разложения). Метод заключается в разложении подинтегральной функции на сумму функций и в почленном интегрировании этой суммы, используя свойство 3 неопределенного ин­теграла. Метод применяется в тех случаях, когда интегралы от отдель­ных слагаемых вычисляются проще, чем от суммы в целом. Пример.

Здесь метод разложения привел к упрощению вычислений.

Здесь метод разложения привел бы нас к ненужному усложнению вы­числений.

3.

2. Интегрирование по частям. Выведем сначала рабочую формулу для этого метода. Пусть и и v — две дифференцируемые функции аргумента х. Тогда, как известно, . Отсюда ,или . Включая произвольное постоянное слагаемое в состав одного из интегралов правой части последнего равенства, получим формулу .

Метод интегрирования по частям заключается в следующем. Предложенный к вычислению неопределенный интеграл мы приводим к виду , причем так, чтобы по выражению мы смогли най­ти первообразную функцию v (т.е. смогли бы проинтегрировать выражение dv); заметим, что здесь нам достаточно найти какую-нибудь одну из первообразных.

После этого применяем к нашему интегралу формулу (7.8) в предположении, что вычисление интеграла окажется проще, чем вычисление интеграла , или что окажется подобным интег­ралу (с коэффициентом, отличным от единицы). Заметим при этом, что для получения окончательного результата может иной раз потребоваться применение метода интегрирования по частям последовательно несколько раз.

3. Интегрирование подстановкой (преобразование переменной). Метод заключается в преобразовании аргумента подынтегральной функции по не­которой формуле, рассчитанной на то, чтобы интеграл в новой переменной оказался проще для вычисления. Например, при вычислении интеграла целесообразно применить подстановку , так как тогда интеграл в новой перемен­ной t оказывается табличным:

.Ниже будет доказано, что новый интеграл равен старому; тогда

. Итак, пусть для вычисления неопределенного интеграла от непрерывной функции f{x) произведена подстановка: , где функция монотонная и имеет непрерывную производную; обозначим через обратную функцию, существование и непрерывность которой следуют из предположенной нами монотонности и непрерывности подстановочной функции . В силу нашей подстановки , . Заме­няя f(x) и dx их новыми выражениями, мы приводим исходный интеграл к виду , где есть непрерывная функция аргумента t.

35. . Интегрирование рациональных дробей.

Можно сформулировать общее правило интегрирования любой рациональной дроби.

Выделяем из рациональной дроби, если она не является правильной(т.е. если степень числителя больше или равна степени знаменателя), целую часть в виде многочлена т(х), поделив для этого числитель на знаменатель, и представляем дробь как сумму многочлена т(х) и правильной рациональной дроби.

Разлагаем знаменатель этой правильной дроби на множители и в соответствии с этим разложением разлагаем дробь на сумму элементарных дробей.

Интегрируем затем многочлен т(х) и полученную сумму элементарных дробей.

Как многочлен т(х), так и все элементарные рациональные дроби интегрируются в элементарных функциях. Следовательно, интеграл от всякой рациональной дроби также вычисляется в элементарных функциях.

Пример. Вычислить интеграл .

Выделяем целую часть т (х) = 4х + 5 и представляем подинтегральную дробь в виде суммы . Разлагаем правильную дробь на сумму элементарных: . Вычисляем теперь I: .
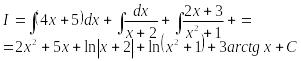