30. Теорема Лагранжа, коши

Теорема Лагранжа Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а,b), то существует такая точка с{а,b), что

Следствие 1. Если производная функции равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.

Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.

Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.

Теорема Коши: Если y = f(x) и у = у(х) - две функции, непрерывные на отрезке [а, b] и дифференцируемые в интервале (а, b) причем ф'(x) не равно 0 для любого х(а, b), то между а и b найдется такая точка с, что

31, Экстремум функции

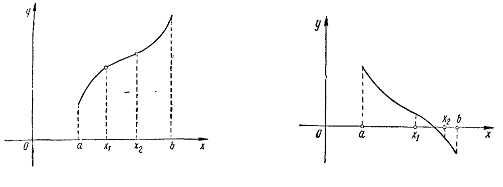
Функция называется возрастающей в промежутке , если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует и большее значение функции.

Таким образом, если то Аналогично функция называется убывающей в промежутке , если для двух любых значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции.

Если то Те значения аргумента, при которых функция достигает своих наиболь­ших или наименьших, по сравнению с соседними, значений, называются точками максимума и минимума.

Определение. Точка называ­ется точкой максимума функции , а значение называется максимумом этой функции, если существует некото­рая окрестность точки [т. е. проме­жуток ], такая, что зна­чение функции в любой точке этой ок­рестности будет меньше, чем ее значение в самой точке , т. е. меньше, чем максимум : при (5.3)

 Аналогично (с заменой слова «меньше» на «больше») определяются точка минимума и минимум функции. Если — точка минимума, a мини­мум, то имеют место следующие неравенства:

при (5.4)

Максимум и минимум функции представлены на рис. 5.4 и 5.5.

Точки минимума и максимума объединяются под общим названием точек экстремума, а минимум и максимум функции объединяются общим названием экстремум функции.

Экстремумы функции , опреде­ленные выше с помощью неравенств (5.3) и (5.4), часто называются стро­гими экстремумами, в отличие от нестро­гих, где предполагаются неравенства вида и соответственно .

Таким образом, понятия максимума и минимума функции носят харак­тер локальных (местных), а не абсолютных понятий.

32. Первообразная функции, интеграл и его свойства

Определение. Функция F(x) называется первообразной для данной функ­ции f{x), если F'(x)=f(x), или, что то же, если dF(x)=f(x)dx.

Пример. Первообразными для функции , определенной в двух непересекающихся промежутках (х<0) и (х>0), служат функции вида F(x) = +С(х), где С(х) — кусочно-постоянная функция: С(х)≡С₁ при х<0,

С(х)=С₂ при х>0, С₁ и С₂— произвольные действительные числа.

О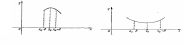 пределение. Совокупность всех первообразных для данной функции f(x), определенной в некотором промежутке или на некотором отрезке конечной или бесконечной длины, называется неопределенным интегралом от функ­ции f(x) [или от выражения f(x)dx ] и обозначается символом .

Если F(x) есть одна из первообразных для f(x), то согласно теореме о первообразных ,(7.1)где С есть произвольная постоянная.

По определению первообразной F'(x)=f(x) и, следовательно, dF(x)=f(x) dx. В формуле (7.1), f(x) называется подинтегральной функцией, а f(x) dx — подынтегральным выражением. Рассмотрим основные свойства неопределенного, интеграла.

1. Дифференциал от неопределенного интеграла равен подинтегральному выражению f(x) dx: .

В самом деле, согласно (7.1), .

2. Неопределенный интеграл от дифференциала некоторой функ­ции и(х) равен этой функции плюс произвольная постоянная:

.

В самом деле, в качестве одной из первообразных годится, очевидно, функ­ция и(х), а тогда неопределенный интеграл от du(x) будет равен, согласно (7.1), сумме и(х)+С.

Пример. .

3. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых функций: (7.4)

Пример. здесь С₁, С₂, С₃ и С—символы произвольной постоянной.

4. Постоянный множитель (отличный от нуля) можно выносить из-под знака неопределенного интеграла: (7.5)

Пример. . Здесь c и С- символы произвольной постоянной.

5. Если , то , (7.6)

где и(х) — произвольная дифференцируемая функция.

Свойство 5 есть прямое следствие свойства инвариантности дифференциала , согласно которому dF(u)—F'(u) du=f(u) du, если dF(x)=F'(x) dx=f(x) dx.