36.Интегрирование выражений, содержащих тригонометрические функции.

В случае, когда подынтегральная функция представляет собой целую степень тригонометрической функции или произведение целых степеней применяют приемы, основанные на использовании формул тригонометрии и на применении общих методов интегрирования.

1) Интеграл от нечетной положительной степени синуса и косинуса.

,

..

2) Интеграл от четной положительной степени синуса и косинуса.

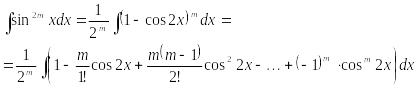
получим конеч­ное число интегралов от четных и от нечетных степеней cos2x. В случае четной степени, снова воспользуемся формулой тригонометрии а в случае нечетной степени применим прием 1). Через конечное число шагов придем к сумме табличных интегралов.

3) Интеграл от произведения целых положительных степеней синуса я косинуса.

Приемы интегрирования целой положительной степени синуса и коси­нуса, изложенные в пунктах 1) и 2), достаточны для интегрирования произ­ведений таких степеней, как это следует из приводимых ниже примеров.

4) Интеграл от нечетной положительной степени секанса и косеканса.

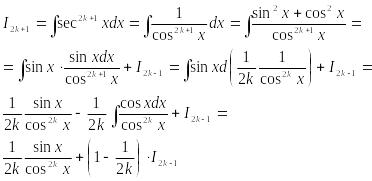
Значит

Получена рекуррентная формула. Последовательно применяя эту фор­мулу, получим выражение через , — через и т. д.;

наконец, — через . Используя теперь полученные нами выражения в обратном порядке, найдем .

5) Интеграл от четной положительной степени секанса и косеканса.

..

Развернув (k— 1)-ю степень двучлена l + tg²x, придем к сумме табличных интегралов.

6) Интеграл от целой положительной степени тангенса и котангенса.

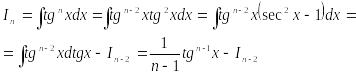
Получена рекуррентная формула .

37. Универсальная тригонометрическая подстановка.

Функция с переменными sin x и cos x, над которыми выполняются рациональные действия( сложение, вычитание, сложение, деление) принято обозначать R( sin x; cos x),где R- знак рациональной функции.

Вычисление неопределенных интегралов типа ∫R( sin x; cos x) dx сводится к вычислению интегралов от рациональной функции подстановкой tg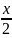 = t,которая называется универсальной.

Правила подстановки:

Если функция R( sin x; cos x) нечетна относительно sin x, т.е. R( -sin x; cos x) = -R( sin x; cos x), то подстановка cos x= t рационализирует интеграл;

Если функция R( sin x; cos x)нечетна относительно cos x, т.е. R(sin x; -cos x) = -R( sin x; cos x), то делается подстановка sin x= t;

Если функция R( sin x; cos x) четна относительно sin x и cos x R( -sin x; -cos x) = R( sin x; cos x), тоинтеграл рационализируется подстановкой tg x = t. Такая же подстановка применяется, если интеграл имеет вид ∫R( tg x ) dx.

38. Интегрирование иррациональностей.

1. Вычисление интегралов вида: ,

где  R —символ   рациональной   зависимости.   Подинтетральная   функция -рациональная функция от аргумента х и нескольких дроб­ных степеней одной и той же дробно-линейной функции этого аргумента х. Применяется подстановка:

где  В — общее наименьшее кратное чисел .

Эта подстановка приводит все подинтегральное выраже­ние к рациональному виду.

Из равенства , х выражается рационально через t; обозначается он так: . Тогда , где r'(t) есть рациональная функция t, как производная от рациональной функции r(t).

,

где — целое число, т.к. В делится без остатка на каждое из чисел  Имеем:

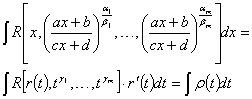,где  есть рациональная функция аргумента t.

2. Вычисление интегралов от рациональной функции  аргумента  х и квадратного радикала из  квадратного  двучлена: .

Вычисление таких интегралов производится с помощью соответствую­щей тригонометрических подстановок:

₁₎ , в случае интеграла ;

2) , в случае интеграла

3) , в  случае интеграла ..

Во всех трех случаях подрадикальное выражение превращается в точ­ный квадрат, радикал исчезает, а интеграл получает вид