73. Теорема умножения вероятностей.
Теорема умножения: Вероятность произведения событий равна вероятности одного из этих событий, умноженной на условную вероятность другого при условии, что первое событие уже произошло.
Р(А В) = Р(А) РА(В). (2.1)
Доказательство:
n – число всех исходов испытания.
m – число исходов, благоприятствующих наступлению события А.
к – число исходов, благоприятствующих наступлению события В, при условии, что А имело место, т.е. к – число исходов, когда А и В наступили вместе.
Поэтому
Р(А
В)
=
=
=
=
P(A)
PA(B).
Теорема умножения вероятностей обобщается на случай произвольного числа событий:
Р(АВСD) = Р(А)· РА(В) ·РАВ(С) · РАВС(D), (2.2)
т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Пример 2. Вероятность попадания в цель для первого стрелка равна 0,8, для второго – 0,7, для третьего – 0,9. Каждый из стрелков делает по одному выстрелу. Какова вероятность того, что в мишени три пробоины?
Решение. Обозначим события: Аi - попадание в цель i-го стрелка (i=1,2,3); В – в мишени три пробоины. Очевидно, что В=А1А2А3, причем события А1, А2, А3 - независимы. По теореме умножения для независимых событий
Р(В) = Р(А1А2А3) = Р(А1) ·Р(А2) ·Р(А3) = 0,8·0,7·0,9 = 0,504.
74. Схема Бернулли повторных испытаний. Формула Бернулли.
Теория вероятностей имеет дело с такими экспериментами, которые можно повторять, по крайней мере теоретически, неограниченное число раз. Пусть некоторый эксперимент повторяется n раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений часто называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:
результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей»;
вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний.
Теорема Бернулли. Если производится серия из n независимых испытаний Бернулли, в каждом из которых успех появляется с вероятностью р, то вероятность того, что успех в n испытаниях появится ровно m раз , выражается формулой
Pn(m)=Cnmpmqn-m, где q=1-p – где вероятность неудачи.
Эта формула называется формулой Бернулли.
75. Локальная и интегральная теоремы Лапласа.
Одно из возможных приближений даёт локальная теорема Муавра-Лапласа (ЛТМЛ).
ЛТМЛ.
◄Пусть случайная величина μn
– число успехов в схеме Бернулли из n
испытаний с вероятностью успеха в
отдельном испытании p
(0 < p
<
1), q
= 1 – p
и величина
,
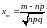где m
- целое число от 0 до n.
Тогда при n→∞:
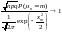
равномерно по всем m, для которых |xm|≤C<∞ при некотором C>0. ►
Возможно, формулировка становится ясна не сразу, тем не менее практический смысл теоремы прост: при больших значениях n вероятность наблюдать ровно m успехов можно приближённо рассчитывать по следующей формуле:
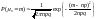
Если вас интересует вероятность того, что число успехов будет лежать в некоторых пределах – P(m1 ≤ μn ≤ m2) – в рассчётах помогает интегральная теорема Муавра-Лапласа (ИТМЛ).
ИТМЛ. ◄ Для схемы Бернулли с вероятностью успеха p в отдельном испытании, 0<p<1, q=1-p при n→∞:
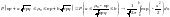
равномерно по a, b; -∞ ≤ a ≤ b ≤ ∞. ►
Смысл: при больших значениях n вероятность P(m1 ≤ μn ≤ m2) можно рассчитывать следующим образом:
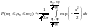
Определение. С.в. X имеет стандартное нормальное распределение (обозначается X~N(0,1)), если её функция распределения задаётся следующим образом:
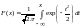
Соответственно, функция плотности для такой с.в. выглядит так:
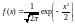
Определение. С.в. X имеет нормальное распределение с параметрами μ и σ2 (обозначается X~N(μ; σ2)), если её функция распределения задаётся следующим образом:
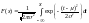
Соответствующая функция плотности:
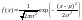
Т.о. стандартное нормальное распределение – частный случай нормального распределения с параметрами μ=1, σ2=1.