
- •5. Векторы, основные определения, понятия, действия над ними
- •9. Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение
- •15. Предел числовой последовательности.
- •16. Предел функции, его геометрическая интерпретация, действия над пределами.
- •17. Первый и второй замечательный предел
- •18. Бесконечно малые величины, их свойства, эквивалентность.
- •19. Раскрытие неопределённостей
- •20. Непрерывность функции.Основные определения, теоремы
- •21. Точки разрыва
- •22. Свойство непрерывных функций на сегменте
- •23. Определение производной
- •24. Правила дифференцирования
- •25. Дифференциал функции
- •26. Производные высших порядков
- •27. Правило Лопиталя.
- •28. Применение производных к исследованию
- •30. Теорема Лагранжа, коши
- •31, Экстремум функции
- •32. Первообразная функции, интеграл и его свойства
- •33.Таблица интегралов
- •34. Методы вычисления неопределенного интеграла (непосредственное интегрирование, подстановкой, по частям).
- •35. . Интегрирование рациональных дробей.
- •36.Интегрирование выражений, содержащих тригонометрические функции.
- •37. Универсальная тригонометрическая подстановка.
- •38. Интегрирование иррациональностей.
- •39. Определенный интеграл как предел интегральных сумм.
- •40. Формула Ньютона- Лейбница. Свойства определенного интеграла.
- •41. Методы вычислений определенного интеграла( непосредственное, подстановкой, по частям).
- •42. Приложения вычислений определенного интеграла ( вычисление площади плоской фигуры, объема тела вращения, длины кривой).
- •57. Дифференциальные уравнения 1 порядка, задача Коши.
- •58 Линейные дифференциальные уравнения первого порядка
- •59 Однородные ду первого порядка
- •60 Ду, допускающие понижение порядка.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •62 Структура общего решения линейного неоднородного дифференциального уравнения.
- •63. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами с правой частью специального вида. Метод неопределенных коэффициентов.
- •71. Классификация событий. Сумма, произведение событий, их свойства, графическое представление.
- •72. Различные определения вероятности.
- •73. Теорема умножения вероятностей.
- •74. Схема Бернулли повторных испытаний. Формула Бернулли.
- •75. Локальная и интегральная теоремы Лапласа.
- •77. Закон распределения вероятностей дискретной случайной величины. Числовые характеристики.
- •78.Законы распределения: биномиальный, Пуассона, равномерный, показательный, нормальный.
- •79. Числовые характеристики дискретных и непрерывных случайных величин.
- •80. Статистическое распределение выборки. Полигон и гистограмма.
1.Определителем
(d) второго
порядка называется число, которое
находится и обозначается так: .
Определителем третьего порядка
называется число, которое находится и
обозначается так, его можно подсчитать
2 способами:1. Правило треугольников.
.
Определителем третьего порядка
называется число, которое находится и
обозначается так, его можно подсчитать
2 способами:1. Правило треугольников.
2.
Правило дописывания элементов.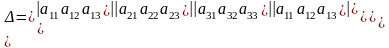

Свойства
определителя.
1)Если строка или столбец в определители
состоит из нулей, то определитель равен
0. 2)Если в определители две одинаковые
строки (столбцы) то d=0
3)Общий множитель строки столбца можно
вынести за скобку 4)d
не измениться, если к элементам
соответствующей строки добавить
соответствующие элементы другой
строки или столба умноженное на одно
и тоже число. 5)Если в определителе какая
– либо строка (столбец) может быть
представлен в виде двух слагаемых то
сам определитель может быть представлен
в виде суммы двух определителей, в
которых все элементы такие же как в
исходном определителе кроме указанной
строки (столбца). В первом определителе
стоят первые слагаемые во втором вторые.
6)Если в определителе поменять местами
две строки (столбца), то определитель
изменит знак на противоположный. 7)Если
в определителе две строки (столбца)
пропорциональны то он равен 0. 8)При
транспонирование значение определителя
не меняется. Транспонирование – это
замена строк столбцами и наоборот.
9)Опр-ль равен сумме произведений
элемента какой-л. строки (столбца) на
их алгебраическое дополнение; зная,
что минором
элемента
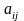 называется
d
полученный из исходного вычеркиванием
i
строки и j
столбца.
называется
d
полученный из исходного вычеркиванием
i
строки и j
столбца.
 ,а
алгебраическим
дополнением
элемента
называется
его минор взятый с определённым знаком.
,а
алгебраическим
дополнением
элемента
называется
его минор взятый с определённым знаком.
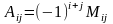 Например,
Например,
2.
Таблица чисел состоящая из m
строк и
n
столбцов называется матрицей.
Числа aij,
составляющие матрицу, называются ее
элементами.
Элементы,
стоящие на диагонали, идущей из верхнего
угла, образуют главную
диагональ. Матрицы
равны
между собой, если
равны все соответствующие элементы
этих матриц, т. е. А
=
B,
если aij
= bij
Матрица,
у которой число строк равно числу
столбцов, называется квадратной.
Квадратную
матрицу размера пхп
называют
матрицей п-го
порядка. Квадратная
матрица, у которой все элементы, кроме
элементов главной диагонали, равны
нулю, называется диагональной.
Диагональная
матрица, у которой каждый элемент
главной диагонали равен единице,
называется единичной
(обозначается
буквой Е).
Квадратная
матрица называется треугольной,
если
все элементы, расположенные по одну
сторону от главной диагонали, равны
нулю. Матрица, все элементы которой
равны нулю, называется нулевой
(обозначается
буквой О).
Матрица,
содержащая один столбец или одну строку,
называется вектором
(или
вектор-столбец, или вектор-строка
соответственно). Матрица, полученная
из данной заменой каждой ее строки
столбцом с тем же номером, называется
матрицей транспонированной
к
данной. Обозначается АТ.
Так,
если
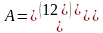 Транспонированная
матрица обладает следующим свойством:
(АT)T
= А.
Транспонированная
матрица обладает следующим свойством:
(АT)T
= А.
Обратная
матрица
матрицы А наз. матрица А-1,
такая, что А*А-1=Е=А-1*А,
если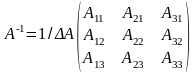 Матрица А наз. невырожденной,
если ее определитель = 0. Ранг
матрицы
– это наивысший порядок определителя,
отличный от 0.
Матрица А наз. невырожденной,
если ее определитель = 0. Ранг
матрицы
– это наивысший порядок определителя,
отличный от 0.
Действия:
Сложение:
матрицы (М) «+» или «-» одинакового
размера по правилу А±В=С =
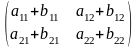
Умножение на число λ: в отличие от опр-ля при умножении М. на число умножаются все элементы.
Св-ва М. при сложении и умножении на число: 1)А+В=В+А(переместит.); 2)(А+В)+С=А+(В+С)(сочетательн.); 3)λ(А+В)=λА+λВ(распределительное); 4)А+0=А; 5)А-А=0; 6)1*А=А
Две матрицы наз.эквивалент., если одна из них получается из другой с помощью элементарных преобразований (А˜ В)
Произведение
М.
М. перемножаются согласно правилу:
элементы строки одного слогаемого
перемножаются с соответствующими
элементами столбца 2 сомножителя и
складываются А*В=С
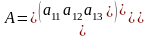 ,
,
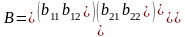 ,
,
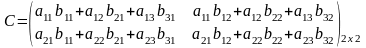
3. Системой линейных алгебраических
уравнений (СЛАУ), содержащей
m уравнений n неизвестных наз. такая
сис-ма вида: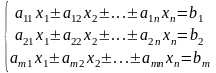 В
матричном виде: А*Х=В, где А-матрица,
состоящая из коэффициентов при
неизвестных, X-матрица,
состоящая из неизвестных, В – матрица
столбец, состоящая из свободных членов.
Методы решения: 1)
Правило Крамара
(если система неоднородна, т.е. свобдые
члены не равны и не равны 0): если d
В
матричном виде: А*Х=В, где А-матрица,
состоящая из коэффициентов при
неизвестных, X-матрица,
состоящая из неизвестных, В – матрица
столбец, состоящая из свободных членов.
Методы решения: 1)
Правило Крамара
(если система неоднородна, т.е. свобдые
члены не равны и не равны 0): если d то система имеет одно единственное
решение, которое можно найти по формулам
Крамара
то система имеет одно единственное
решение, которое можно найти по формулам
Крамара
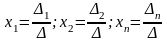 В
этих формулах
В
этих формулах
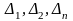 это определители, полученные из основного
определителя заменой соответствующего
столбца на столбец свободных членов.
Основной определитель системы равен
0, а хотя бы один из определителей
это определители, полученные из основного
определителя заменой соответствующего
столбца на столбец свободных членов.
Основной определитель системы равен
0, а хотя бы один из определителей
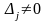 то система не имеет решений. Определитель
равен 0
то система не имеет решений. Определитель
равен 0
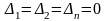 , бесконечное множество решений.
2) Метод Гаусса. Нужно
смотреть всегда, не пришла ли система
к виду 0x1+0x2….+0xn=b,
b
не равно 0.(не имеет решений) Далее
приводим систему к ступенчатому виду
и смотрим, не появилось ли это уравнение.
И приводим систему к ступенчатому виду.
Если система принимает вид
треугольника),число лесенок совпадает
с числом неизвестных ) то система имеет
одно единственное решение
, бесконечное множество решений.
2) Метод Гаусса. Нужно
смотреть всегда, не пришла ли система
к виду 0x1+0x2….+0xn=b,
b
не равно 0.(не имеет решений) Далее
приводим систему к ступенчатому виду
и смотрим, не появилось ли это уравнение.
И приводим систему к ступенчатому виду.
Если система принимает вид
треугольника),число лесенок совпадает
с числом неизвестных ) то система имеет
одно единственное решение
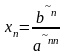 . Если система к треугольному виду не
привелась т.е остаётся ступенчатый
вид, то она имеет бесконечное множество
решений. Для однородной системы линейных
уравнений при решении методом гаусса
если число уравнений меньше числа
неизвестных то система имеет не нулевое
решение. 3)
Метод обратной матрицы.
Обратная
матрица
матрицы А наз. матрица А-1,
такая, что А*А-1=Е=А-1*А,
если
,
поэтому изначально находится определитель
матрицы А, потом ее алгебраические
дополнения и подставляются в данную
формулу А-1.
. Если система к треугольному виду не
привелась т.е остаётся ступенчатый
вид, то она имеет бесконечное множество
решений. Для однородной системы линейных
уравнений при решении методом гаусса
если число уравнений меньше числа
неизвестных то система имеет не нулевое
решение. 3)
Метод обратной матрицы.
Обратная
матрица
матрицы А наз. матрица А-1,
такая, что А*А-1=Е=А-1*А,
если
,
поэтому изначально находится определитель
матрицы А, потом ее алгебраические
дополнения и подставляются в данную
формулу А-1.
4. Комплексным числом z называется выражение вида z=x+iy, где x, y – действительные числа, а i – мнимая единица, i2=-1. Эта форма записи называется алгебраической. Модуль r и аргумент φ комплексного числа можно рассматривать как полярные координаты вектора r = ОМ, х = rcosφ, y = rsinφ. Тогда z = r (sinφ+isinφ). Эта форма записи называется тригонометрической. Используя формулу Эйлера eiφ=cosφ+isinφ комплексное число z = r (cosφ+isinφ) можно записать в показательной форме: z = r eiφ, где r = |z|- модуль комплексного числа, а угол φ = Arg z = argz + 2πk (k=0,-1,1,-2,2,…). Сложение z1+z2=(x1+x2)+i(y1+y2); вычитание z = z1-z2=(x1-x2)+i(y1-y2); произведение z1z2=(x1x2-y1y2)+i(x1y2+y1x2) или z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)); возведение в степень zn=(r(cosφ+isinφ))n=rn(cosnφ+isinnφ);
;
извлечение корней
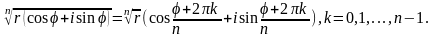
5. Векторы, основные определения, понятия, действия над ними
Определение
1.
Направленный отрезок будем называть
вектором и обозначать
![]()
Определение
2.
Вектор называется нулевым, если его
начало и конец совпадают и обозначают
![]()
Отметим, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет нам при записи отождествлять нулевой вектор с вещественным числом нуль.
Определение 3. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
Определение 4. Два вектора называются равными, если выполнены следующие три условия: 1) длины векторов равны, 2) векторы параллельны (коллинеарны), 3) векторы направлены в одну и ту же сторону.
Определение 5. Два вектора называются противоположными, если для них выполнены первые два условия определения 4, а третье условие нарушается.
Сложение векторов
Суммой
![]() двух векторов
двух векторов
![]() называется вектор, идущий из начала
вектора
называется вектор, идущий из начала
вектора
![]() в конец вектора
в конец вектора
![]() при условии, что вектор
приложен к концу вектора
(правило треугольника) и записывают
при условии, что вектор
приложен к концу вектора
(правило треугольника) и записывают
![]() (смотри рис.3.1).
(смотри рис.3.1).
Сложение векторов обладает следующими основными свойствами:
1. Коммутативность: + = +
2.
Ассоциативность: для любых векторов
,
и
![]() выполняется равенство
выполняется равенство
![]()
3.
Прибавление нулевого вектора к любому
вектору
не меняет последнего:
![]()
4. Сумма вектора и противоположного вектора 1 равна нулевому вектору, т. е. + 1 =0
Вычитание векторов
Разностью двух векторов и называется такой третий вектор , что = + и обозначает - = .
чтобы из одного вектора вычесть другой, нужно их отнести к общему началу и провести вектор из конечной точки вектора – вычитаемого в конечную точку вектора – уменьшаемого
Умножение вектора на число и его свойства
Определение.
Произведением α
(или
α)
вектора
на вещественное число
![]() называется вектор
,
коллинеарный вектору
,
(причем вектор
имеет длину, равную │
││
│)
и имеющий направление, совпадающее с
направлением вектора
в
случае
›
0 и противоположное направление в случае
‹ 0.
называется вектор
,
коллинеарный вектору
,
(причем вектор
имеет длину, равную │
││
│)
и имеющий направление, совпадающее с
направлением вектора
в
случае
›
0 и противоположное направление в случае
‹ 0.
Операция умножения вектора на число обладает следующими свойствами:
1. ( + ) = + (распределительное свойство числового сомножителя относительно суммы векторов).
2. ( + β) = α + β (распределительное свойство векторного сомножителя относительно суммы чисел).
3. a(β ) = (αβ) (сочетательное свойство числовых сомножителей).
6.
Длиной
вектора называется арифметическое
значение квадратного корня и скалярного
квадрата.
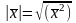
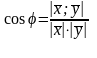 .
Чтобы сложить вектора, заданные в
координатной форме необходимо сложить
их соответствующие координаты, если
необходимо произвести вычетание
векторов, то мы из координат конца
вектора вычитаем соответственные
координаты начала вектора. При умножении
вектора, заданного в координатной форме
необходимо каждую его координату
умножить на это число.
.
Чтобы сложить вектора, заданные в
координатной форме необходимо сложить
их соответствующие координаты, если
необходимо произвести вычетание
векторов, то мы из координат конца
вектора вычитаем соответственные
координаты начала вектора. При умножении
вектора, заданного в координатной форме
необходимо каждую его координату
умножить на это число.
7.
Векторы, лежащие на одной прямой или
на параллельных прямых, называются
коллинеарными
(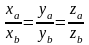 ,
векторное произведение =0) Векторы a
b
c
называются компланарными,
если они лежат в одной плоскости или
же находятся в параллельных плоскостях.
(a*b)c=0
– компланарны
,
векторное произведение =0) Векторы a
b
c
называются компланарными,
если они лежат в одной плоскости или
же находятся в параллельных плоскостях.
(a*b)c=0
– компланарны
8.
Скалярным произведением двух
ненулевых векторов называется число,
равное
произведению этих векторов на косинус
угла между ними.
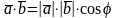 ,
,
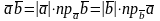 Свойства:
Свойства:
1.
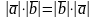 ,
2.
,
2.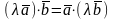 ,
3.
,
3.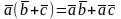 ,4.
,4.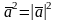 .
Векторное произведение векторов и его
свойства.Три
некомпланарных вектора образуют правую
тройку
если с конца третьего поворот от первого
вектора ко второму совершается против
часовой стрелки. Если по часовой – то
левую.
Векторным
произведением
вектора
.
Векторное произведение векторов и его
свойства.Три
некомпланарных вектора образуют правую
тройку
если с конца третьего поворот от первого
вектора ко второму совершается против
часовой стрелки. Если по часовой – то
левую.
Векторным
произведением
вектора
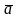 на вектор
на вектор
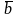 называется
вектор
называется
вектор
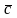 ,
который: 1. Перпендикулярен векторам
и
.2.
Имеет длину, численно равную площади
параллелограмма, образованного на
векторах
и
.
,
который: 1. Перпендикулярен векторам
и
.2.
Имеет длину, численно равную площади
параллелограмма, образованного на
векторах
и
.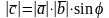 ,
где
,
где
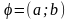 .
Векторы
,
и
образуют правую тройку векторов.
Свойства:1.
.
Векторы
,
и
образуют правую тройку векторов.
Свойства:1.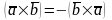 ,2.
,2. ,3.
,3.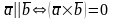 ,
4.
,
4.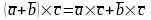 ,
,
 Смешанное
произведение
записывают в виде:
Смешанное
произведение
записывают в виде:
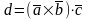 .Смысл
смешенного произведения: сначала два
вектора векторно перемножают, а затем
полученный скалярно перемножают с
третьим вектором. Смешанное произведение
представляет собой число – число.
Результат смешанного произведения –
объем параллелепипеда, образованного
векторами. Свойства.1.
Смешанное
произведение не меняется при циклической
перестановке сомножителей:
.Смысл
смешенного произведения: сначала два
вектора векторно перемножают, а затем
полученный скалярно перемножают с
третьим вектором. Смешанное произведение
представляет собой число – число.
Результат смешанного произведения –
объем параллелепипеда, образованного
векторами. Свойства.1.
Смешанное
произведение не меняется при циклической
перестановке сомножителей:
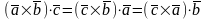 ,
2. Смешанное произведение не изменится
при перемене местами векторного и
скалярного произведения.
,
2. Смешанное произведение не изменится
при перемене местами векторного и
скалярного произведения.
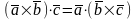 Смешанное
произведение меняет знак при перемене
мест любых двух векторов-сомножителей.
Смешанное
произведение меняет знак при перемене
мест любых двух векторов-сомножителей.

Три
вектора называются компланарными, если
результат смешанного произведения
равен нулю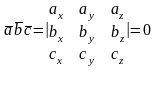 Геометрический смысл. Смешанное
произведение некомпланарных векторов
Геометрический смысл. Смешанное
произведение некомпланарных векторов
![]() ,
,
![]() и
и
![]() по модулю равно объему параллелепипеда,
построенного на этих векторах.
по модулю равно объему параллелепипеда,
построенного на этих векторах.
