17. Первый и второй замечательный предел

Теорема. (раскрывает неопределенность типа 0/0).

Второй замечательный предел - иррациональное число.

18. Бесконечно малые величины, их свойства, эквивалентность.

Функция a(x) называется бесконечно малой при x®a, если , т.е. если для "e>0 существует d>0, что для всех 0<½x-а½<d, выполняется неравенство ça(x) ç<e. Бесконечно малую функцию ça(x) ç называют также бесконечно малой величиной.

Свойства бесконечно малых функций

1. Если функции a₁(x) и a₂(x) бесконечно малые, то сумма функций a₁(x)+ a₂(x) также есть бесконечно малая функция. Функция f(x) называется ограниченной при x®a, если существуют положительные числа М и d, такие, что при условии 0<½x-а½<d выполняется неравенство .Любая бесконечно малая функция a(x) является ограниченной функцией при x®a.

2. Произведение ограниченной при x®a функции на бесконечно малую, есть функция бесконечно малая.

3. Произведение постоянной на бесконечно малую есть бесконечно малая.

4. Произведение двух бесконечно малых есть бесконечно малая функция.

19. Раскрытие неопределённостей

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов , , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Для раскрытия неопределённостей типа используется следующий алгоритм:

Выявление старшей степени переменной;

Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

Разложение на множители числителя и знаменателя;

Сокращение дроби.

Для раскрытия неопределённостей типа иногда удобно применить следующее преобразование:

Пусть и

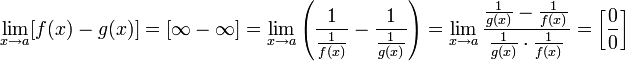
20. Непрерывность функции.Основные определения, теоремы

Пусть y=f(x) определена в некотором интервале (а, b), x₀ и x – два произвольных значениях аргумента из этого интервала. Обозначим x–x₀=Dx откуда x=x₀+Dx. Говорят, что для перехода от значения аргумента x₀ к значению x, первоначальному значению придано приращение Dx.

Приращением Dy функции y=f(x), соответствующем приращению Dx аргумента x в точке x₀, называется разность D y=f (x₀ +Dx)-f (x₀)

Определение. Функция y=f(x) называется непрерывной в точке x₀, если бесконечно малому приращению Dx аргумента x в точке x₀ соответствует бесконечно малое приращение функции D y т.е.

Определение. Если функция непрерывна в каждой точке отрезка [а, b], то она непрерывна на этом интервале. Теорема 1. Если функции f₁ (x) и f₂ (x) непрерывны в точке x₀, то непрерывны в этой точке также их алгебраическая сумма f₁(x)± f₂(x), произведение f₁(x) f₂(x) и при условии f₂(x₀)≠0 частное (аналогично теоремам о пределах).

Теорема 2. Если функция u=j(x) непрерывна в точке x₀, а функция y=f(u) непрерывна в точке u₀=j(x₀), то сложная функция y=f(j(x)) непрерывна в точке x₀.