
- •10. Дифференцируемость функции в точке. Функции, дифференцируемые на интервале и их свойства: Теоремы, Роля, Лагранжа.
- •11. Дифференцируемость функции в точке. Функции, дифференцируемые на интервале и их свойства: Теоремы, Роля, Лагранжа.
- •12. Экстремум функции одной переменной. Необходимые и достаточные условия экстремума.
- •Направление выпуклости графика функции
- •Точки перегиба графика функции
- •13. Формула Тейлора для функции одной переменной.
- •15. Функции многих переменных. Ограниченность функции. Предел функции многих переменных.
- •16. Функции многих переменных. Непрерывность. Свойства непрерывных функций.
- •17. Дифференцируемость функции многих переменных. Частные производные. Связь между дифференцируемостью и непрерывностью частных производных.
- •18. Производные функции по направлению, градиент.
- •19. Экстремум функции многих переменных. Необходимые и достаточные условия экстремума.
- •Примеры исследования функции на экстремум.
- •20. Формула Тейлора для функции одной и многих переменных.
- •20. Условный экстремум.
- •22. Неявные функции, теорема о неявной функции. Производная неявной функции.
- •23.Определенный интеграл Римана, сумма Дарбу, критерий интегрируемости. Простейшие свойства интеграла Римана. Интегральные суммы. Интегрируемость.
- •§2.Верхние и нижние суммы.
- •Основные св-ва определенного интеграла.
- •24. Методы вычисления определенного интеграла. Формула Ньютона-Лейбница
- •27. Несобственные интегралы, критерий Коши сходимости несобственных интегралов. Признаки сходимости: признак сравнения, признаки Абеля и Дирихле.
- •32. Формулы Грина, Стокса и Остроградского.
- •34. Функции комплексного переменного. Предел функции. Непрерывность.
34. Функции комплексного переменного. Предел функции. Непрерывность.
Комплексным
числом z
называется
выражение вида
![]() ,
где x
и y
– любые
действительные числа, а i
– мнимая
единица, удовлетворяющая условию
,
где x
и y
– любые
действительные числа, а i
– мнимая
единица, удовлетворяющая условию
![]() .
Числа x
и y
называются
соответственно действительной
и мнимой
частями
комплексного числа z
и обозначаются
.
Числа x
и y
называются
соответственно действительной
и мнимой
частями
комплексного числа z
и обозначаются
![]() .
.
Комплексное число
![]() называется сопряженным
комплексному
числу
.
называется сопряженным
комплексному
числу
.
Комплексные числа
![]() и
и
![]() cчитаются
равными тогда и только тогда, когда
cчитаются
равными тогда и только тогда, когда
![]() ,
,![]() .
.
Суммой
![]() двух комплексных чисел
и
называется
комплексное число
двух комплексных чисел
и
называется
комплексное число
![]() .
.
Разностью
![]() двух комплексных чисел
двух комплексных чисел
![]() и
и
![]() называется комплексное число
называется комплексное число
![]() .
.
Произведением
![]() двух комплексных чисел
и
называется комплексное число
двух комплексных чисел
и
называется комплексное число
![]() .
.
Частным
![]() от деления комплексного числа
на комплексное число
от деления комплексного числа
на комплексное число
![]() называется такое комплексное число z,
которое
удовлетворяет уравнению
называется такое комплексное число z,
которое
удовлетворяет уравнению
![]() ,
т.е.
,
т.е.
![]() .
.
Говорят, что на
множестве
![]() задана функция
задана функция
![]() ,
если задан закон, по которому каждой
точке
,
если задан закон, по которому каждой
точке
![]() ставится в соответствие одно (однозначная
функция) или несколько (многозначная
функция) значений
ставится в соответствие одно (однозначная
функция) или несколько (многозначная
функция) значений
![]() .
.
Пусть
и
![]() .
Тогда задание функции комплексного
переменного
равносильно заданию двух функций
действительных переменных
.
Тогда задание функции комплексного
переменного
равносильно заданию двух функций
действительных переменных
![]() ,
,
![]() .
.
Пример 1.
Найти действительную
и мнимую части функции
![]() .
.
Решение.
Полагая , , получим
![]() .
.
Следовательно,
![]() - действительная часть,
- действительная часть,
![]() - мнимая часть
функции
.
- мнимая часть
функции
.
Пример 2.
В какую кривую
отображается окружность
![]() с помощью функции
с помощью функции
![]() .
.
Решение.
Зададим окружность
с помощью полярных координат:
![]() ,
,![]() .
Тогда,
.
Тогда,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() .
Значит, образом окружности
в плоскости z
будет
окружность
в плоскости w,
проходимая дважды.
.
Значит, образом окружности
в плоскости z
будет
окружность
в плоскости w,
проходимая дважды.
Элементарные функции комплексного переменного.
1. Дробно-рациональная функция
![]() .
.
Показательная функция комплексного переменного задается формулой:
![]() .
.
Показательная функция обладает следующими свойствами:
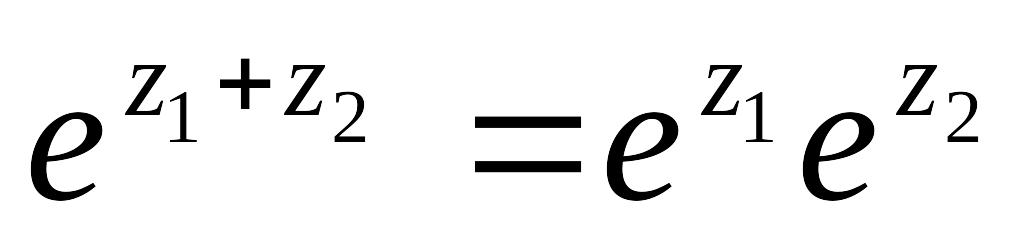 ,
где
и
- любые комплексные числа;
,
где
и
- любые комплексные числа;
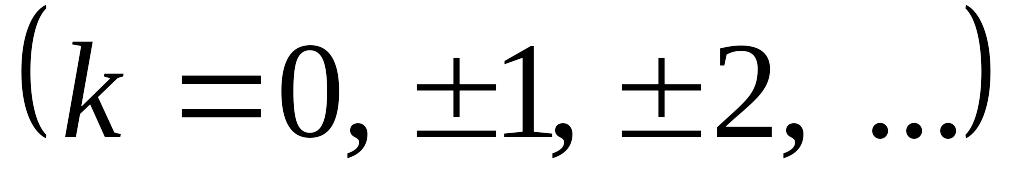 ,
т.е показательная функция является
периодической с чисто мнимым периодом
,
т.е показательная функция является
периодической с чисто мнимым периодом
 .
.
Тригонометрические функции
 и
и
 определяются формулами:
определяются формулами:
![]() ,
,
![]() .
.
Функции
и
![]() - периодические с действительным периодом
- периодические с действительным периодом
![]() и имеют только действительные нули
и имеют только действительные нули
![]() и
и
![]() ,
соответственно.
,
соответственно.
Функции
![]() и
и
![]() определяются равенствами :
определяются равенствами :
![]() ,
,
![]() .
.
Для тригонометрических функций комплексного переменного остаются в силе все известные формулы тригонометрии.
Гиперболические функции
 ,
,
 ,
,
 ,
,
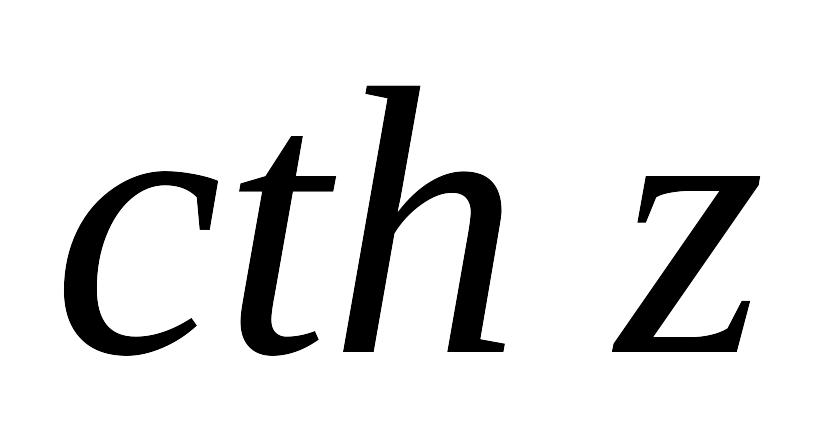 определяются равенствами :
определяются равенствами :
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тригонометрические и гиперболические функции связаны между собой следующими соотношениями:
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Логарифмическая функция
 ,
,
 ,
определяется как функция, обратная к
показательной, причем
,
определяется как функция, обратная к
показательной, причем
![]() ,
.
,
.
Эта функция является
многозначной. Главным
значением
называется
то , которое получается при
![]() и обозначается
и обозначается
![]() .
.
Очевидно,
![]() ,
.
,
.
Логарифмическая функция обладает следующими свойствами:
![]() ,
,
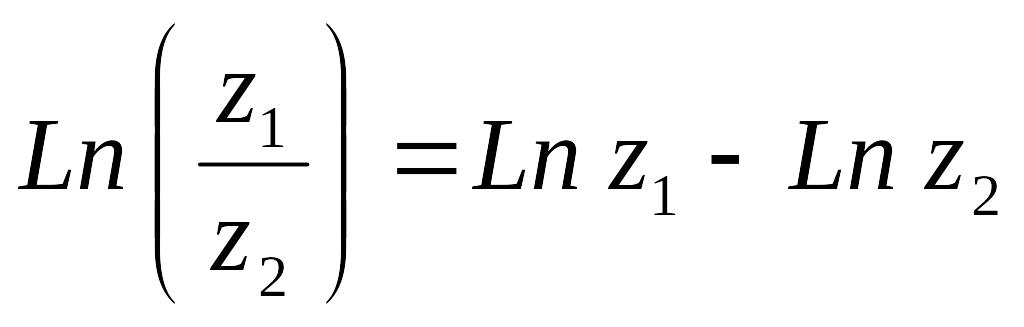 .
.
Обратные тригонометрические функции
 ,
,
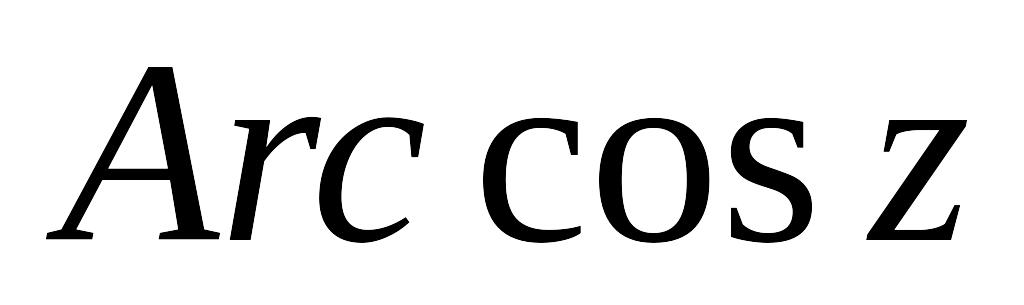 ,
,
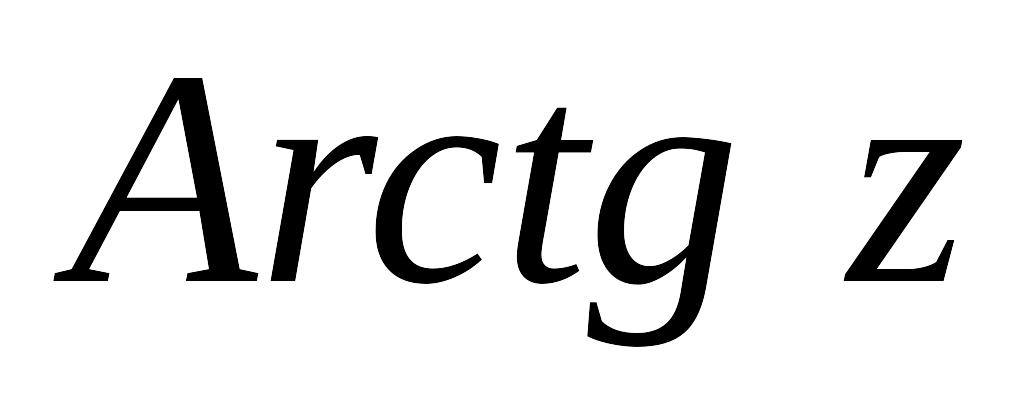 ,
,
 определяются как функции, обратные
соответственно к функциям
определяются как функции, обратные
соответственно к функциям
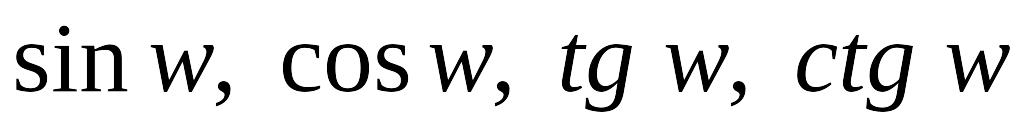 .
Так , если
.
Так , если
 ,
то
называется
арксинусом числа
,
то
называется
арксинусом числа
 и обозначается
и обозначается
 .
Все эти функции являются многозначными
и выражаются через логарифмические:
.
Все эти функции являются многозначными
и выражаются через логарифмические:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Главные значения
обратных тригонометрических функций
![]() ,
,
![]() ,
,
![]() ,
,
![]() получаются, если брать главные значения
соответствующих логарифмических
функций.
получаются, если брать главные значения
соответствующих логарифмических
функций.
Общая степенная функция
 ,
где
,
где
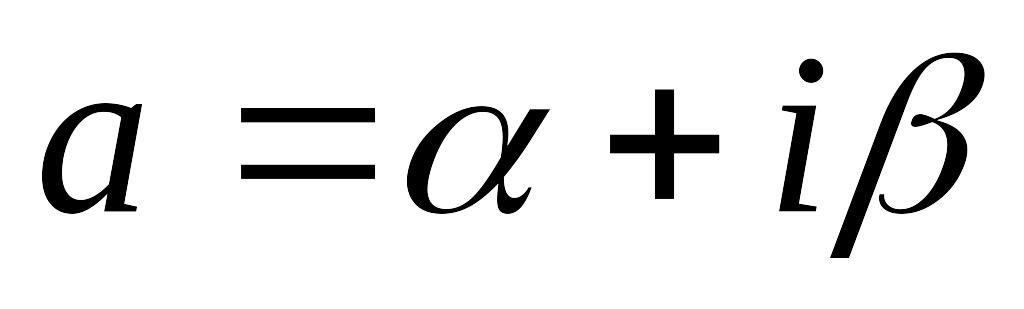 - любое комплексное число, определяется
соотношением
- любое комплексное число, определяется
соотношением
![]() .
.
Эта функция
многозначная, ее главное значение
![]() .
.
Общая показательная функция
 ,
где
,
где
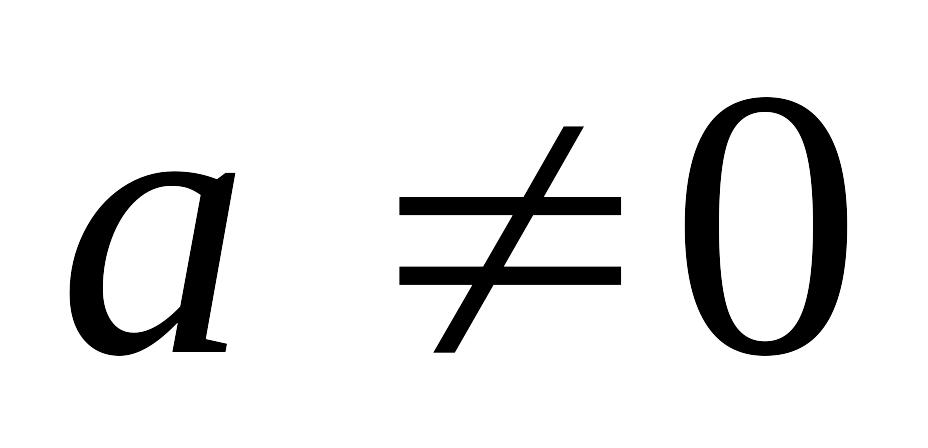 -
любое комплексное число, определяется
равенством
-
любое комплексное число, определяется
равенством
![]() .
.
Главное значение
этой функции
![]() .
.
Пример 1.
Найти значение
модуля функции
![]() в точке
в точке
![]() .
.
Решение.
Так как , то
![]() .
.
Тогда
![]()
=![]() .
.
Полагая
![]() ,
найдем
,
найдем
![]() .
.
Как видим, тригонометрическая функция комплексного переменного может принимает значения, по модулю большие единицы.
