Матан

1. Числовые множества. Верхний и нижний предел числовых множеств.

Числовым множеством называется множество, элементами которого являются числа. Иными словами, числовое множество – это совокупность каких-либо чисел.

Допустим, Х – существующее множество действительных чисел. Множество Х называется ограниченным снизу, если существует такое число а, что для любого хХ выполняется а≤х. Множество Х называется ограниченным сверху, если существует такое число а, что для любого хХ выполняется а≥х.

Число М называется верхней гранью числового множества, если выполняются следующие условия: 1) х≤М для любого хХ 2) для любого έ>0 существует такое число хХ, что х>M- έ. Верхняя грань числового множества обозначается sup X.

Число М называется нижней гранью числового множества, если выполняются следующие условия: 1) х≥М для любого хХ 2) для любого έ>0 существует такое число хХ, что х<M+ έ. Верхняя грань числового множества обозначается inf X.

2. Функции. Предел Функции.

Допустим, Х – множество элементов х, У – множество элементов у. Если каждому элементы х Х поставлен в соответствие единственный элемент у У, обозначаемый у=f(x), то говорят, что на множестве Х задана функция у=f(x), где значения х Х называют значениями аргумента, а значения у У называют значениями функции.

Функция, заданная в виде у=f(x) называют явной функцией. Функция заданная формулой F(x,y)=0 называют неявной функцией.

Пусть дана функция у=f(x), определенная на интервале, содержащем точку х=а. Число А называется пределом функции у=f(x) при х стремящемся к а если для любого числа ἑ>0 существует такое число δ>0, что при всех х, удовлетворяющих условию 0<|x-a|< δ выполняется неравенство

|f(x) – A|< ἑ

Нельзя забывать, что ἑ и δ – отличные от нуля, но стремящиеся к нему очень маленькие числа.

Иными словами, предел функции – это наиболее близкое значение, которое принимает функция в окрестности аргумента, к которому стремится функция.

Предел функции обозначается через:

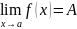
3. Бесконечно малые функции и их свойства.

Функция α=α(x) называется бесконечно малой при х→а (или при х→∞), если 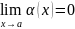. Бесконечно малые функции имеют смысл лишь при стремлении аргумента к какому либо числу или бесконечности. Например, бесконечно малой является функция 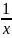при х→∞.

Свойства бесконечно малых функций описываются следующими теоремами:

Теорема 1. Если функция у=f(x) имеет предел b при х→a, то

у=b+α, y(x)=b+α(x),

где α=α(x) – бесконечно малая функция при х→a.

Теорема 2 Произведение бесконечно малой на ограниченную функцию есть бесконечно малая функция.

Следствие 1 Произведение двух бесконечно малых функций есть бесконечно малая функция.

Следствие 2 Произведение бесконечно малой на постоянную функцию есть бесконечно малая функция.

4. Основные теоремы о пределах функции.

В процессе решения практических и абстрактно-теоретических задач, содержащих пределы, помогут некоторые основные теоремы, описывающие свойства предела функции.

Теорема 1. Функция у=у(х) при х→а не может иметь более одного предела.

Теорема 2. Если две функции имеют пределы, то сумма, разность и произведение этих функций так же имеют пределы, причем:

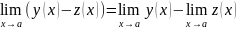
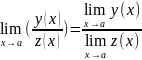
Следствие 1. Если каждое слагаемое алгебраической суммы имеет предел при х→а, то сумма таких слагаемых так же имеет предел и этот предел равен сумме пределов слагаемых.

Следствие 2. Постоянный множитель можно выносить за знак предела.

Теорема 3. Если функция при х→a имеет положительный (отрицательный) предел, то функция в окрестности этой точки так же положительная (отрицательна).