4. Непрерывность функции. Точки разрыва, их классификация.

Функция у=f(x), определенная на интервале (а,b) называется непрерывной в точке, принадлежащей этому интервалу, если предел функции равен её значению при предельном значении аргумента.

Разность называется приращением аргумента.

Иными словами, функция непрерывна в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Точка разрыва – это точка, в которой функция определена, но не является непрерывной. Существуют следующие виды точек разрыва.

Если – точка разрыва и существуют конечные пределы , , то такая точка называется точкой разрыва первого рода.

Если функция у=f(x) имеет разрыв в точке и , то точка называется точкой устранимого разрыва. Если видоизменить или доопределить такую функцию, то получится функция, непрерывная в точке .

Если – точка разрыва и по крайней мере один из пределов является бесконечным или не существует, то точка называется точкой разрыва второго рода.

4. Предел последовательности.

Число а называется пределом последовательности, если для любого числа έ>0 найдется такое натуральное число N, что при всех n>N выполняется неравенство

Последовательность, имеющая предел, называется сходящейся, а последовательность, у которой нет предела – расходящейся.

Предел постоянной равен постоянной.

Теорема 1. Если последовательность имеет предел, то она ограниченна.

Теорема 2. Всякая ограниченная сверху (снизу) монотонно возрастающая (убывающая) последовательность имеет предел, причем этот предел равен верхней (нижней) грани этой последовательности.

4. Первый и второй замечательные пределы.

Первый замечательный предел имеет вид:

Это означает, что при бесконечно малых значениях аргумента мы для удобства вычислений можем опустить функцию синуса и работать непосредственно с числом.

Второй замечательный предел имеет вид:

Эти пределы мы можем использовать для упрощения вычислений и избавления от разного рода неопределенностей.

4. Некоторые важные пределы.

Очень часто при решении задач с пределами приходится отказываться от базовых методов решения. В данном случае необходимо использовать несколько важных пределов, которые помогут упростить задачу или избавиться от неопределенностей:

.

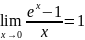
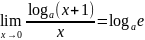В ряде случаев удается при помощи этих важных пределов упростить решение предела, путем приведения примера к данному виду.

4. Понятие производной. Ей геометрический и физический смысл.

Производной функции y=f(x) называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю.

Производная от данной точки равна тангенсу угла между осью Ox и касательной к графику функции в данной точке.

Кроме того, производная пути по времени равна скорости прямолинейного движения точки.

4. Производные некоторых функций.

Для нахождения производных используется специальная таблица производных:

4. Основные правила дифференцирования

4. Основные формулы дифференцирования. Производные высших порядков.

Формулы дифференцирования – вопрос 10.

Производной второго порядка функции y=f(x) называется производная от её производной, т.е.

Аналогично производную от второй производной называют производной третьего порядка или третьей производной.

В общем случае производной n-го порядка называется производная от производной (n-1)-го порядка: .

Производные второго третьего и более высоких порядков называют последовательным дифференцированием данной функции.

4. Основные теоремы дифференциального исчисления (Лагранжа, Коши, Ролля)

Теорема Ролля. Если то имеется такая точка , что .

Теорема Лагранжа. Существует такая точка 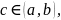что

Теорема Коши. Если , то существует такая точка , что

4. Правило Лопиталя-Бернулли.

Правило Лопиталя-Бернулли служит для раскрытия различных неопределенностей.

Если , при условии что предел в правой части выражения существует. Аналогично и для производных высшего порядка.

Если , при условии, что предел в правой части существует. Аналогично и для производных высшего порядка.

Иными словами, правило Лопиталя можно использовать сколько угодно раз до получения необходимого результата.

4. Формула Тейлора.

Пусть функция у=f(x) определена в некоторой точке х=а и в некоторой окрестности этой точки имеет все производные до (n+1)-го порядка, тогда существует точка х=έ, такая что выполняется формула Тейлора

Последнее слагаемое называется остаточным членом в форме Лагранжа. Формула Тейлора при а=0 называется формулой Маклорена.

4. Признаки постоянства, возрастания и убывания функции.

Исследования функций невозможны без исследований производных.

Если y=f(x) дифференцируема на отрезке, которому принадлежит данная точка х и f’(x)≥0 (f’(x)≤0), то функция не возрастает (не убывает) на данном интервале.

Иными словами, если f’(x)>0, то функция возрастает, если f’(x)<0, то функция убывает на данном интервале.

4. Экстремум функции. Необходимые и достаточные условия экстремума функции.

Точками экстремума называются точки локального максимума или минимума.

Значение называется локальным максимумом (минимумом) функции, если для любого достаточно малого δ выполняется условие для любого .

Необходимое условие: Если функция имеет в точке локальный экстремум то производная этой точке обращается в ноль или не существует.

Первое достаточное условие экстремума. Если при переходе через критическую точку слева направо производная меняет знак с плюса на минус (с минуса на плюс), то такая функция имеет в этой точке локальный максимум (минимум). Если же не меняет своего знака, то функция в этой точке не имеет экстремума.

Второе достаточное условие экстремума. Если первая производная в точке равна нулю, а вторая производная не равна нулю, то такая функция имеет экстремум, причем, если вторая производная меньше нуля, то точка – локальный максимум. Если больше нуля, то точка является локальным минимум.