MathCad_Labs

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ И НАУКЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ СИБИРСКОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА

ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

Учебное пособие

Красноярск 2007

УДК 51(07)

В93 Теория вероятностей и математическая статистика: лабораторный практикум / И. И. Вайнштейн, Т. А. Кустицкая, Т. В. Сидорова

Данное учебное пособие по лабораторному практикуму предназначено для студентов специальности "Прикладная математика"и охватывается следующие разделы математической статистики: основные понятия математической статистики, точечные оценки случайных величин, интервальное оценивание, проверка статистических гипотез, корреляционный и дисперсионный анализ, линейные и нелинейные статистические модели.

Содержит теоретические сведения, методические указания по выполнению лабораторных работ в среде Mathcad и варианты заданий к лабораторным работам.

Перед выполнением лабораторных работ студенту необходимо ознакомиться с представленными теоретическими сведениями и подробно разобрать приведенные примеры решения соответствующих задач в среде Mathcad.

@ Коллектив авторов, 2007 Печатается в авторской редакции

2

Cодержание

1.3Выборочные характеристики . . . . . . . . . . . . . . . . . 7

1.4Задание к лабораторной работе . . . . . . . . . . . . . . . . 10

4Проверка гипотезы о виде распределения с помощью

4.1Статистическая гипотеза и статистический критерий. Критерий согласия. . . . . . . . . . . . . . . . . . . . . . . . . . 22

4.2Критерий Смирнова для проверки гипотезы о виде распре-

5Проверка параметрической гипотезы о виде распреде-

5.1Критерий согласия Пирсона . . . . . . . . . . . . . . . . . . 28

5.2Задание к лабораторной работе . . . . . . . . . . . . . . . . 31

3

9.1Однофакторный дисперсионный анализ . . . . . . . . . . . 55

9.2Двухфакторный дисперсионный анализ . . . . . . . . . . . 58

9.3Задание к лабораторной работе . . . . . . . . . . . . . . . . 60

9.4Варианты заданий . . . . . . . . . . . . . . . . . . . . . . . 60

10 Метод наименьших квадратов. Построение конкретных

10.1Нелинейная регрессия . . . . . . . . . . . . . . . . . . . . . 71

10.2Задание к лабораторной работе . . . . . . . . . . . . . . . . 73

4

Лабораторная работа 1. Первичная обработка экспериментальных данных

1.1Основные понятия выборочного метода

Пусть G - эксперимент, связанный со случайной величиной ξ, имеющей распределение F. Рассмотрим n независимых повторений эксперимента

Gи обозначим X1, X2 . . . , Xn совокупность полученных наблюдений. Вектор X = (X1, X2, . . . , Xn) называется выборкой объема n из со-

вокупности с распределением F. (Символически это можно обозначить

X F).

Рассмотрим случайную величину ξ , имеющую дискретное распределение F , которое сосредоточено в точках X1, X2, . . . , Xn, и для которого

1

вероятность значения Xi(i = 1, 2 . . . , n) равна n. Функцию распределения Fn можно записать так:

Fn - эмпирической функцией распределения.

Если элементы выборки X упорядочить по возрастанию, то получится последовательность

X(1) ≤ X(2) ≤ · · · ≤ X(n),

которая называется вариационным рядом.

По нему можно построить эмпирическую функцию распределения

5

При возрастании объема выборки эмпирическая функция распределения неограниченно приближается к функции распределения исходного распределения F. Об этом гласят следующие теоремы:

Теорема 1.2 (Гливенко-Кантелли) Пусть X = (X1, . . . , Xn) - выборка объема n из неизвестного распределения с функцией распределения F . Пусть Fn - эмпирическая функция распределения, построенная по этой выборке. Тогда

sup F (y) F (y) P 0 при n .

| n − | → → ∞

y R

Вэтих теоремах имеет место сходимость по вероятности.

1.2Гистограмма и полигон

Разделим область выборочных данных на интервалы 1, 2, . . . , k. Обозначим за νj(j = 1, 2, . . . , k) число элементов выборки, попавших в интервал j:

го пропорциональна νj. Общая площадь всех прямоугольников должна быть равна единице.

6

Пусть lj - длина интервала j. Высота hj прямоугольника над интервалом j равна

νj hj = nlj.

Верхний контур полученной фигуры, состоящий из горизонтальных отрезков называется гистограммой. Имеет место следующая теорема о приближении гистограммы к функции плотности распределения:

Теорема 1.3 Если плотность распределения элементов выборки является непрерывной функцией, то при неограниченном увеличении числа

k(n)

интервалов группировки (k(n) → ∞, так что n → 0) имеет место сходимость по вероятности гистограммы к плотности распределения.

Если гистограмму модифицировать следующим образом - соединить отрезками прямых середины горизонтальных отрезков, то полученная ломанная является графиком непрерывной функции и называется полигоном частот. Здесь середины крайних отрезков (соответствующие 1 и k) соединяются с осью абсцисс так, чтобы по-прежнему суммар-

ная площадь под графиком равнялась единице.

1.3Выборочные характеристики

Выборочным моментом порядка k называется величина

Выборочный центральный момент порядка k равен

Выборочный момент a1 называется выборочным средним и обозна-

Выборочный момент ao2 называется выборочной дисперсией и обозна-

7

Также большую роль в математической статистике играет несмещенная выборочная дисперсия, которая вычисляется по формуле

Рассмотренные характеристики являются выборочными аналогами неизвестных истинных моментов распределения.

В среде Mathcad предусмотрена возможность генерации последовательности случайных чисел с соответствующим законом распределения. Например, с помощью функции rbinom(n, k,p) генерируется выборка объема n из биномиального распределения Bpk.

Приведем пример построения гистограммы для выборки объема n = 2000 из нормального распределения N0,1 (см. рис. 1.1). Для построения гистограммы область выборочных данных была разбита на 20 равных интервалов.

8

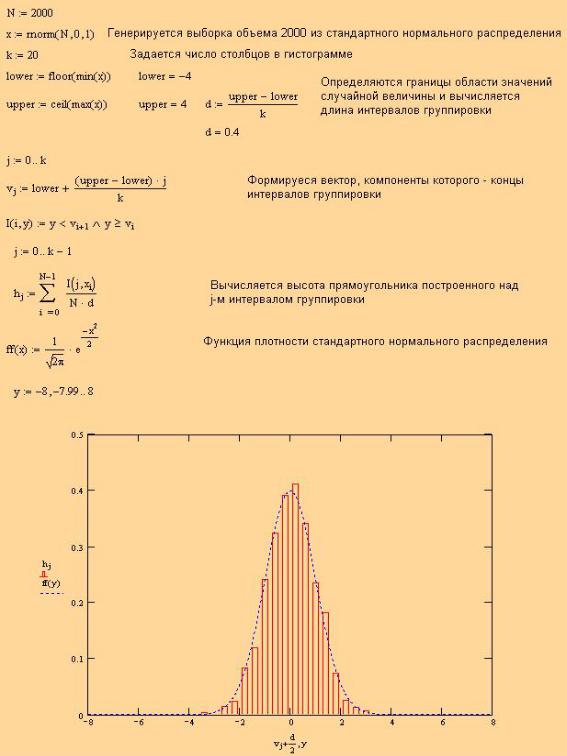
Рис. 1.1. Построение гистограммы для выборки из нормального распределения

При построении гистограммы с помощью шаблона двухмерных графиков соответствующему ряду данных был назначен тип гистограммы. Для этого в диалоговом окне Formatting Currently Selected Graph

(Форматирование) на вкладке Traces (Графики) был установлен тип

9

списка bar (Столбцы).

1.4Задание к лабораторной работе

Сгенерировать выборку из N элементов, имеющих указанное в вашем варианте распределение (см. Приложение А).

1.Вычислить выборочные моменты и центральные выборочные моменты до 3-го порядка включительно.

2.Составить эмпирическую функцию распределения. В одной системе координат построить график эмпирической и теоретической функций распределения. Увеличивая объем выборки с N до 2N, 3N, убедиться

спомощью построенного графика в стремлении эмпирической функции распределения к теоретической.

3.В одной системе координат построить гистограмму и теоретичеcкую функцию плотности распределения (если она является непрерывной), сравнить полученные графики и оценить, действительно ли гистограмма является приближением функции плотности вероятности.

Варианты заданий

1.X - выборка из биномиального распределения Bpn, где p = 0.7, n = 50.

2.X - выборка из равномерного распределения U2,4.

3.X - выборка из показательного распределения Eλ, где λ = 2.

4.X - выборка из распределения Фишера Fk,m, где k = 2, m = 10.

5.X - выборка из нормального распределения Na,σ2 , где a = 2, σ = 1.5.

6.X - выборка из геометрического распределения Gp с параметром

p = 0.75.

7.X - выборка из распределения Стьюдента Tk, где k = 3.

8.X - выборка из распределения Пуассона Πλ, где λ = 3.

10.X - выборка из распределения χ2k, где k = 2.

11.X - выборка из гамма-распределения 1,λ, где λ = 5.

12.X - выборка из бета-распределения βm,n, где m = 2, n = 3.

13.X - выборка из распределения Фишера Fk,m, где параметрами

k = 4, m = 5.

14.X - выборка из биномиального распределения Bpn, где p = 0.3, n = 400.

15.X - выборка из гамма-распределения 1,λ, где λ = 3.

10