1. Способы задания движения материальной точки (МТ). Траектория, скорость, ускорение М.Т.

Движение будем рассматривать в декартовой системе координат. Материальной точкой будем называть объект, формами и размерами которого в условии данной задачи можно пренебречь. Радиус-вектором будем называть вектор

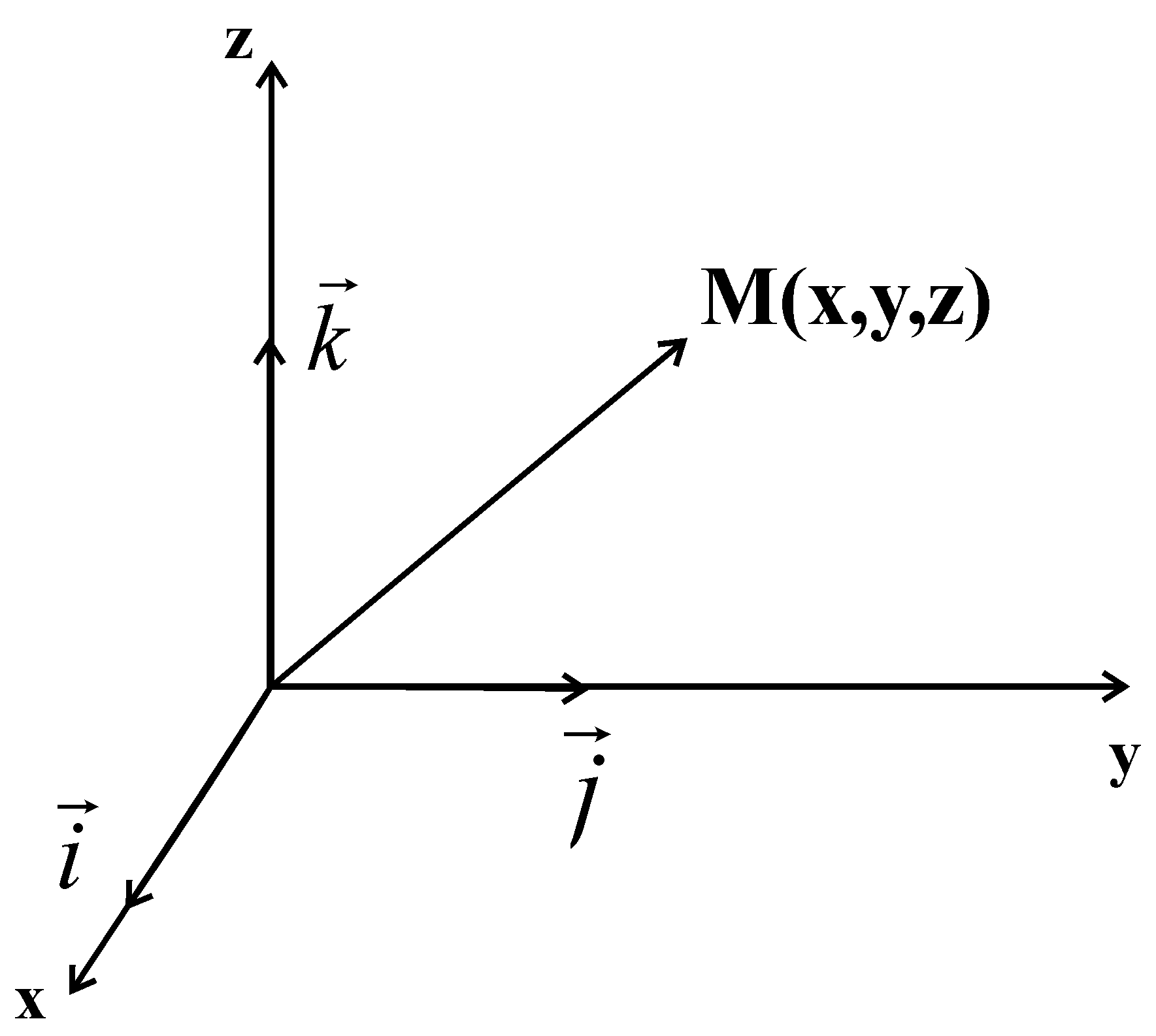
Будем считать, знак движения точки заданным, если будем знать положение точки в любой момент времени.

Рассмотрим способы задания движения материальной точки:

1.  Если тело движется, то его координаты меняются со временем. Задание движения точки в декартовых координатах - это значит задать его координаты x,y,z как функции от времени.

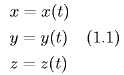
тогда

2.  Естественный способ. Введем понятие траектории. Траектория - это линия, которую описывает материальная точка при своем движении.

На заданной траектории выберем точку А принимая за начало отсчета. Положим точка М относительно точки А определяется длиной дуги AM траектории, которую обозначают через s и будем называть растоянием.

При движении точки по траектории растояние s изменяется и является функцией от времени. Если s(t) известна, то для любого момента времени можно определить положение точки. По самой природе s(t) должна быть однозначной, конечной, непрерывной, дважды дифференцируемой.

3.  Траекторию можно задать в параметрической форме.

Пример.

2. Скорость и ускорение МТ в естественных осях. Движение МТ по окружности.

По определению вектора

где - скорость вдоль траектории.

Из дифференциальной геометрии известно, что предел при равен единичному вектору

касательной.

Тогда (1.5) запишем в виде

где - алгебраическая скорость точки М.

Если возрастает, то Если убывает, то

По первой тореме Серре - Френе справедливо, что

Превая теорема Серре - Френе.

где - единичный вектор главной нормали, - радиус кривизны в данной точке.

Тогда (1.7) запишется в виде

Из (1.8) видно, что ускорение состоит из двух слагаемых, напрвленного по касательной и

ворого направленного по главной нормали

- тангенсальная составляющая.

- нормальная составляющая.

Движение точки по окружности.

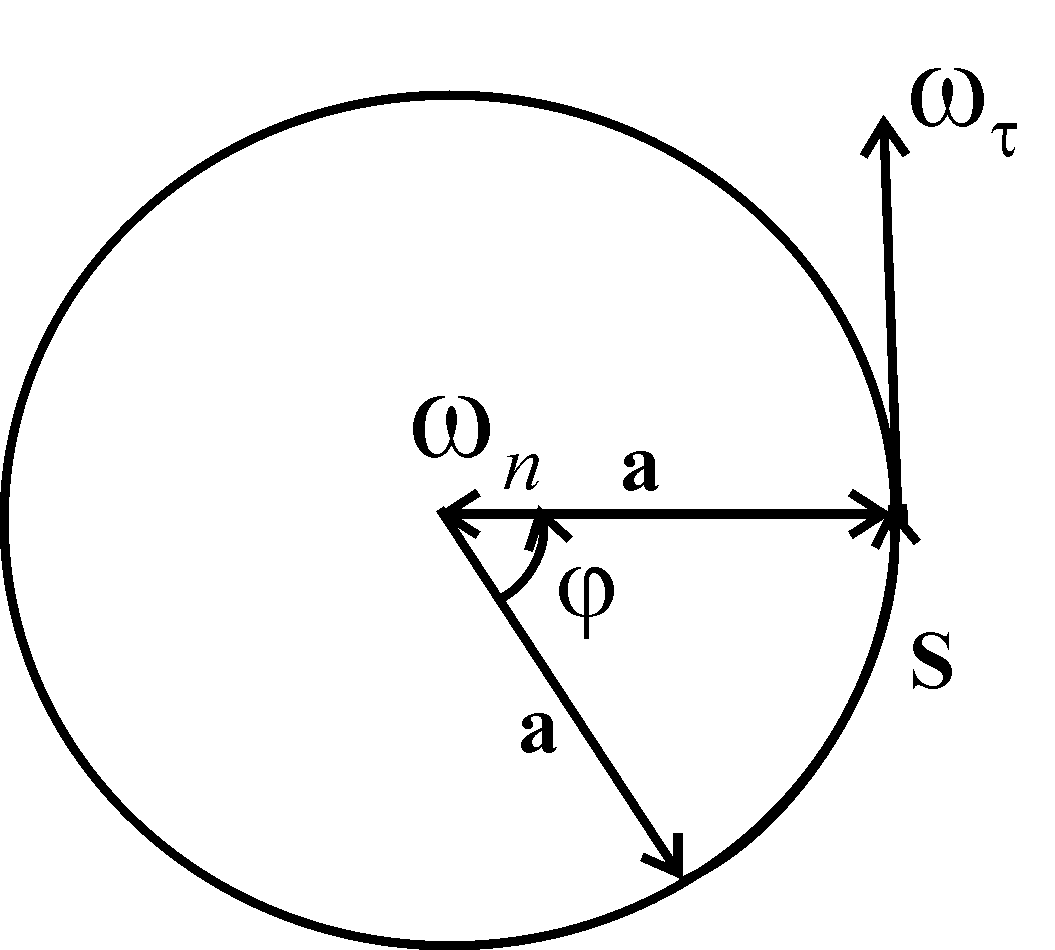
При малых углах

- угловая скорость

Определим тангенсальное ускорение в этом случае.

- угловое ускорение.

Центростремительное ускорение:

3. Скорость и ускорение МТ при задании его движения координатным способом.

Пусть задан закон движения

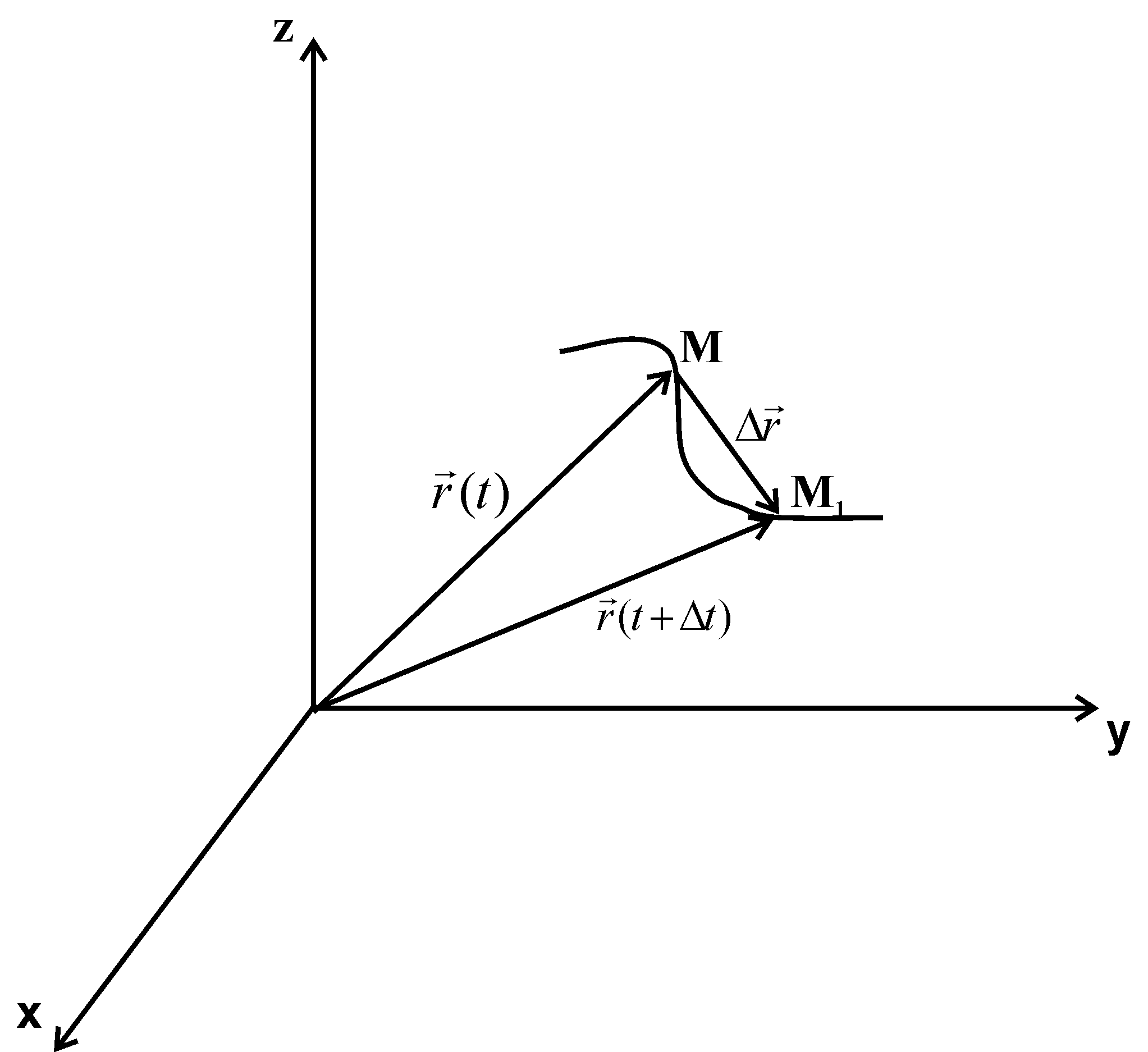
Вектор v называют скоростью.

Учитывая (1.2) можно написать:

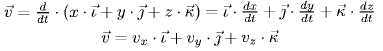
Аналогично определяем ускорение,

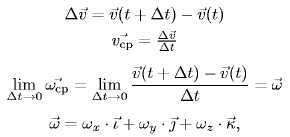
где

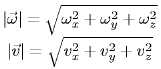
4. Скорость и ускорение МТ при задании его движения векторным способом.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из на­чала координат О в точку М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента :

.

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т. е. годограф этого вектора, определяет траекторию движущейся точки.

5. Способы задания движения АТТ. Степени свободы ТТ. Уравнения движения.

Различают 5 видов движения ТТ:

-поступательное

-вращательное

-плоское или плоскопараллельное

- сферическое

-общий случай движения ТТ

Поступательное и вращательное движения являются простыми движениями ТТ.

Поступательным дв-ем ТТ наз-ся такое движ-ие,при котором любая прямая, проведенная в теле, остается во все время дв-ия параллельной своему начальному положению.

Вращательным дв-ем ТТ наз-ся такое дв-ие, при котором остаются неподвижными все его точки лежащие на некоторой прямой, называемой осью вращения.

Число параметров, однозначно определяющих положение мех. системы, наз-ся числом степени свободы. Если на положение точек не наложено никаких ограничений, то система, состоящая из 1 точки, имеет 3степени свободы, а система состоящая из 2-хточек имеет 6 степеней свободы. В первом случае положение системы определяется 3 координатами точки, во 2м случае 6 координатами 2х точек.

Ограничения, наложенные на положение мех. системы, наз-ся связями. Наложение 1й связи уменьшает число степеней свободы мех. системы.

Уравнениями поступательного дв-ия ТТ явл-ся уравнения дв-ия любой точки этого тела – обычно уравнения дв-ия его центра тяжести с.

. это ур-ие явл-ся уравнением вращ-го дв-ия тела. Это ур-ие полностью определяет положение вращающегося тела в любой момент времени.

6.Поступательное и вращательное движения АТТ.Распределение скоростей и ускорения при вращении АТТ вокруг неподвижной оси.

Поступательным движением ТТ наз-ся такое движение,при котором любая прямая,проведенная в теле,остается во все время дв-ия параллельной своему начальному положению.

Т-ма: все точки ТТ ,движ-ся поступательно, описывают в пр-ве одинаковые траектории и в каждый момент времени имеют один-е ск-ти и уск-ия.

Эта т-ма позволяет описывать дв-ие ТТ,как дв-ие одной точки.Общие для всех точек ск-ть и уск-ие наз-ся ск-тью и уск-ем поступательного дв-ия ТТ. При любом другом виде дв-ия ск-ть и уск-ие точек различаются.

Уравнением поступательного дв-ия ТТ явл-ся любое ур-ие:

Вращательном дв-ем ТТ наз-ся такое дв-ие,при кот. остаются неподвижными все его точки лежащие на нек-ой прямой, называемой осью вращения.

Описание этого дв-ия: через ось вращения z проводятся 2 полуплоскости: неподвижная P и подвижная Q, вращ-ся вместе с ней.

Двухгранный угол между этими полупл-тями, отсчитываемый от неподвижной полупл-ти P к подвижной полупл-ти Q назся углом поворота. Условимся считать угол поворота положит-ым, если смотря на встречу оси вращения можно увидеть его отложенным против дв-ия час. стрелки. Угол определяя положение подвижной полупл-ти Q определяет положение всей вращающейся фигуры. Поэтому этот угол рассм-ся как угол координата тела. При вращении угол меняется как и это ур-ие явл-ся уравнением вращ-го дв-ия тела. Это ур-ие полностью определяет положение вращающегося тела в любой момент времени.

Пусть в момент времени t подвижная полупл-ть Q: t ; Q1: t+ , . Переходя к пределу: , . .

Численная величина, характеризующая быстроту изменения угловой ск-ти, наз-ся угловым ускорением. .

7. Вращательное дв-ие АТТ. Уравнение вращ-го дв-ия. Формулы Эйлера.

Вращательном дв-ем ТТ наз-ся такое дв-ие,при кот. остаются неподвижными все его точки лежащие на нек-ой прямой, называемой осью вращения.

Описание этого дв-ия: через ось вращения z проводятся 2 полуплоскости: неподвижная P и подвижная Q, вращ-ся вместе с ней.

Двухгранный угол между этими полупл-тями, отсчитываемый от неподвижной полупл-ти P к подвижной полупл-ти Q назся углом поворота. Условимся считать угол поворота положит-ым, если смотря на встречу оси вращения можно увидеть его отложенным против дв-ия час. стрелки. Угол определяя положение подвижной полупл-ти Q определяет положение всей вращающейся фигуры. Поэтому этот угол рассм-ся как угол координата тела. При вращении угол меняется как и это ур-ие явл-ся уравнением вращ-го дв-ия тела. Это ур-ие полностью определяет положение вращающегося тела в любой момент времени.

Введем понятия векторов условимся откладывать вектор угл. ск-ти тела от любой точки оси вращения направляя его по этой оси так, чтобы смотря на встречу этому вектору видеть вращение тела происходящую в сторону,обратную вращению час. стрелки. Поэтому этот вектор наз-ся скользящим. Точкой приложения м.б. любая точка оси вращения, тогда яв-ся скользящими.Направление совпадает с направ-ем при ускоренном вращении и противоположно ему при замедленном. Пользуясь понятием угл. ск-ти получим векторное выражение для вращательной ск-ти:

Если смотреть на встречу вектора можно увидеть поворот в-ра к в-ру на угол , соверш-ся в сторону, обратную вращению час.стрелки, т.е. направление вращат-й ск-ти совпадает с направ-ем векторного произведения векторов . .

Если известны проекции вектора угл. ск-ти, направленного по оси вращ-я тела по а и координаты точки x,y,z, то корд-ты вращ. Ск-ти определим из понятия векторного произведения:

;

Формулы Эйлера.

8.Скорости и ускорения точек ТТ,вращ-гося вокруг неподвижной оси. Формулы Эйлера.

ОМ-длина дуги, =R* . Sin =S/R; Sin

- вращательная ск-ть точки.

Из следует,что модули вращ-х скоростей различных точек вращающихся ск-тей пропорционально расстоянию от этих точек до оси вращения. Определим ускорение точки М. это ускорение будет состоять из 2-х составляющих. Определим след.образом:

Касательное ускорение: =R* .

Нормальное ускорение:

.

Из этих формул следует, что модуль вращательных, центростремительных и полных ускорений точек вращ-гося тела пропорционально расстояниям от этих точек до оси вращения. При равномерном вращении . В этом случае ускорение а точки М направлено к центру окр-ти прямой.

Введем понятия векторов условимся откладывать вектор угл. ск-ти тела от любой точки оси вращения направляя его по этой оси так, чтобы смотря на встречу этому вектору видеть вращение тела происходящую в сторону,обратную вращению час. стрелки. Поэтому этот вектор наз-ся скользящим. Точкой приложения м.б. любая точка оси вращения, тогда яв-ся скользящими.Направление совпадает с направ-ем при ускоренном вращении и противоположно ему при замедленном. Пользуясь понятием угл. ск-ти получим векторное выражение для вращательной ск-ти:

Если смотреть на встречу вектора можно увидеть поворот в-ра к в-ру на угол , соверш-ся в сторону, обратную вращению час.стрелки, т.е. направление вращат-й ск-ти совпадает с направ-ем векторного произведения векторов . .

Если известны проекции вектора угл. ск-ти, направленного по оси вращ-я тела по а и координаты точки x,y,z, то корд-ты вращ. Ск-ти определим из понятия векторного произведения:

;

Формулы Эйлера.

9. Плоским или плоскопарал-м движ-ем т.т. назыв-ся такое движение,при которой кажая точка тела движется к плоскости парал-й некоторой неподвижной плоскости. т.к. положения плоской фигуры на плоскости опред-ся положением 2-х ее точек или полож-м отрезка,соедин-го 2 точки этой фигуры,то движение плоской фигуры ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости. Будем считать,чтодвижение плоской фигуры происходит в плоск-ти.

Покажем,что перемещение фигуры можно осуществить совокупностью 2-х перемещений: поступ-е перемещение и поворот.

1) перемещение фигуры поступ-но из положения АВ в полож-е так,чтобы т. A переместилась в новое положение А1,а т.В- вписала траекторию тождеств-ую траекторию т.А. затем повернув фигуру вокруг точки А1 на угол так,чтобы т. совпала с точкой В1.

2) переместим фигуру поступ-но парал-но из положения АВ в положение . Затем повернем ее вокруг точки В1 на угол так,чтобы т. совпала с точкой А1.

Вариантов перемещений может быть столько,сколько точек в плоской фигуре. Т.о. поступ-е перемещение плоской фигуры различно для разных точек,а угол поворота всегда одинаков . Из этого следует что всякое непоступ-е перемещение плоской фигурой ее плоскости можно рассматр-ть как совокупность 2-х перемещений. Поступ-е перемещение плоской фигуры вместе с произвол-й точкой называемой полюсом и поворотом вокруг полюса. При этом поступ-е перемещение зависит от выбора полюса,а числовая величина угла поворота и направ-е поворота от выбора полюса не зависит. Применим т.о. за полюс и запишем Ур-е узкопарал-го движ-я

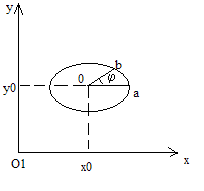
При O(x0,y0) можно опред-ть движ-я полюса О и след-но поступ-е движение всей фигуры ур-ии (3.1.1)

Для получения угла характеристического вращат-ю часть движения плоской фигуры проведем ч/з т.О 2 полупрямые ОА и ОВ так,чтобы ОА не принад-т этой фигуре и движ-ся поступательно с полюсом О,а ОВ принад-т этой фигуре и вращается вместе с ней вокруг полюса О. Обозначим угол можно опред-ть вращат-е движение фигуры. Угловая скорость яв-ся общим для всех полюсов и назыв-ся угловой скоростью и угловым ускорением плоской фигуры. (3.1.2) в-р направ-ны по оси проход-й через полюс перпендик-м плоскости фигуры.

10. Зависимость между скоростями точек плоской фигуры устанав-ся по след-й теореме:

Скорость любой точки плоской фигуры равна геометрич-й сумме скорости полюса и скорости этой точки ее вращений вместе с плоской фигурой вокруг полюса

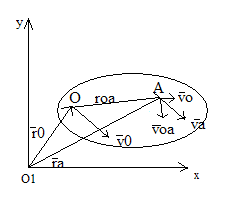
Радиус в-р соед-т 2 точки плоской фигуры. За все время движение этот в-р вращается вокруг полюса с угловой скоростью плоской фигуры неизмен-сь по модулю. , , скорость полюса.

вращается скорость т. А относит-но полюса О.

Вращ-я скорость можно пред-ть в виде . Вращат-я скорость направ-на перпендик-но отрезку ОА сорону вращения и модуль (3.2.1)

1) Док-во сущ-я мгновенного центра скоростей:

Пользуясь терминой о скоростях точек плоск-ти фигуры покажем,что в каждый момент времени сущ-ет точка неизменно связанной с плоской фигуры. Скорость кот-й в этот момент равна 0. эту точку называют мгновенным центром скоростей. Допустим,что известно скорость некот-й точки v0 и угловая скорость в некоторый момент времени. Применим т.о. за полюс. Тогда скорость любой точки фигуры будет равной сумме скорости полюса и вращ-й скорости точки вокруг этого полюса. В основном в т.О перпен-й к направлению скорости v0 так,чтобы направ-е поворота в-ра v0 совпадало к этому перпендик-ру с направ-ем вращения фигуры. Вращ-й скорости точек этого перпенд-ра направ-но противоположно точек этого перпендик-ра направ-но противоположно скорости полюса. Найдем такую точку Р вращ-я скорость ,

След-но, т. Р в рассмат-й момент времени яв-ся мгновенным центром скоростей. Опред-м положение точки Р. (3.3.1)

След-но мгновенный центр скоростей плоской фигуры,наход-ся на перпендик-ре и направ-ю скорости полюса на расст-ии от полюса равным . Скорость любой точки плоской фигуры в каждый момент времени имеют модуль равный произвед-ю скорости фигуры на длину отрезка соед-го точку с мгновенным центром скоростей и направ-й перпенд-но к этому отрезку в сторону вращения фигуры. Модуль скоростей точек плоской фигуры в каждый момент времени пропорц-на расст-ям от этих точек до мгновенного центра скоростей.

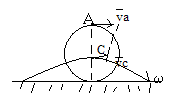
2) различный случаи опред-я полож-я мгновенного центра скоростей.

а)

Направ-е скоростей нам известно. Проводим перпенд-р к направ-ю скоростей.

б)

в) скорости направ-ны парал-но,но в разные стороны

г) тело движется поступ-но

д)

При движении плоской фигуры при котором она катится без скольжения по некоторой неподвижной линии мгновенный центр скоростей наход-ся в точке соприкосания с линией. Это справ-во при отсут-ии скольжения. Мгновенный центр скоростей харак-ет распред-е скоростей точек плоской фигуры в данный момент времени. Запишем для док-ва теорему Шарля: по конечной перемещении плоской фигуры.плоскую фигуру можно переместить из одного полож-я в любое другое положение на плоск-ти одним поворотом этой фигуры вокруг некот-го неподвижного центра.

11. Движение плоской фигуры в ее плоск-ти можно рассмат-ть как совокуп-ть 2-х движ-й в поступ-е движ-е фигуры вместе с полюсом и ее вращением вокруг полюса. Ускорение точек плоской фигуры опред-ся след. теоремой: Ускорение любой точки плоской фигуры ровно геометр-й сумме ускорении полюса и ускорения этой точки в ее вращении вместе с плоской фигурой вокруг полюса.

Для установ-я этой завим-ти допустим вращение каждой фигуры

, , где вращат-я скорость равная . Для нахож-я ускорения продиф-ем (3.4.1) , (3.4.2)

, , , (3.4.3) , , , .

След-е1: Проекция ускорения любой точки плоской фигуры на ось провед-х из произвол-го полюса через эту точку не может быть больше проекции ускорения полюса на ту же ось.

След-е2: Концы ускорений точек любого отрезка лежат на одной прямой и делит эту прямую на части пропоцион-го расстоян-ям между этими точками.

12. Рассм-м движение т.т. одна из точек которого во все время движ-я остается неподвижной. При таком движении все остал-е точки тела движ-ся по сферич-м поверх-тям цнтры которых совпоадют с неподвижной точкой. По этой причине рассмат-мое движение тела назыв-ся сферическим движением т.т. Для опред-я положения тела в кадый момент времени воспол-ся 2-мя системами корд-т: неподвижная Oчня с началом неподвижной т.О и подвижной системой Ox1y1z1 неизменно связанной с т.т. сначала той же неподвиж-й точки.

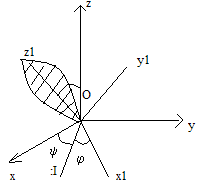
Обозначим линию пересечения неподвижной плоск-ти xoy и подвиж-я x1oy1. Эту линию будем назыв-ть линией узлов. Отметим углы , , . Угол лежит в плоск-ти xoy перпенд-й оси z. Плоск-ть угла перпенд-но оси z1. условимся считать углы , , полож-ми. В случай если смотря на встречу осям z,I,z1 перпенд-ны плоск-тям этих углов можно видеть эти углы отлож-е от осей x,z,I

в сторону обратного вращения часовой стрелки. Заданием углов , , однозначно опред-ся полож-ем подвижной системы осей x1,y1,z1 неизменно связано с твердым телом и след-но полож-е самого т.т. Действит-но,зная углы , , полож-еподвиж-й сист по x1,y1,z1 опред-ся след-м образом: отложив в плоск-ти xoy от осей Ox угол находим линию узлов OI. Отложив от оси Oz плоск-ти проведем через эту ось перпенд-р линии узлов угол получаем ось Oz1. В плоск-ти провед-й через линию узлов перпенд-р оси Oz1. от линии узлов отклад-ем угол и находим Ox1. Ось Oy1 проводим в этой плоск-ти пд прямым углом и оси Ox1. Отложим так,если смотреть ось Oz? в сторону обратного вращ-ю час.стр.. Углы , , назыв-ся Эйлеровыми углами при этом наз-ся углом прецессии, угол , угол собствен-го вращения. Название этих углов заимствованы из астрономии. При движении т.т. (4.1)

Когда одна из его точек остается неподвижной углы , , измен-ся во времени. Эти ур-я (4.1) сферич-го движения т.т. положение т.т в простр-ве опред-ся полож-ем 3-х его точек не лежащих на одной прямой. Действит-но, 2 точки опред-т некоторую ось,а 3-я точка положение тела по отношению к этой оси. След-но, можно опред-ть полож-м 2-х точек не лежащих на одной прямой с неподвиж-й точкой.

Теорема Элера-Далампера. Твердое тело имеющее одну неподвижную точку можно переместить из одного полож-я в любое другое поворотом некоторой оси проход-й через неподвижную точку.Эту ось наз-т осью конечного поворота тела.

. В случае сферич-го движ-я в-р угловой скорости тела в данный момент в-р отклад-ся от неподвижной точки О. Мгновенная ось пред-т собой геометр-е место точек тела скорости которых в данный момент равны 0. В каждую сторону,чтобы смотря в одну сторону в-ра видеть вращение тела происход тело против движ-я часовой стрелки.

14. Составное движение точки. Теорема о сложении скоростей. Теорема о сложении ускорений (Теорема Кориолиса).

Сложное движение точки или тела – это такое движение, при котором точка одновременно участвует в двух или нескольких движениях.

Рассм движущееся тело А и точку и совершающую по отн-ию к нему некоторое движение. Через произвольную точку О движущегося тела проведем неизменно связанные с этим телом оси x, y, z. Систему осей Оxyz наз-ют подвижной системой отсчета. Неподвижной системой отсчета наз-ют систему О₁ξηζ, связанную с некоторым неподвижным телом (обычно с Землёй).

Движение точки М относит-но неподвижной системы отсчета называют абсолютным движением точки.Скорость и ускорение точки в абсолютном движении наз-ют абсолютной скоростью и абсолютным ускорением .

Движение точки М относит-но подвижной системы отсчета наз-ют относительным движением точки. Скорость и ускорение точки в относительном движении наз-ют относительной скоростью и относительным ускорением .

Движение в подвижной системе отсчета Оxyz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета О₁ξηζ явл-ся для точки М переносным движением.

Точки тела А, совершая различные движения, имеют в данный момент различные скорости и ускорения. Скорость и ускорение точки тела А, связанного с подвижной системой отсчета, совпадающих в данный момент с движущейся точкой, называют переносной скоростью и переносным ускорением точки М.

Движение точки М по отн-ию к неподвижной системе отсчета, которое наз-ся абсолютным движением, явл-ся сложным, состоящим из относительного и переносного движений точки.

Основная задача изучения сложного движения состоит в установлении зависимости м/у скоростями и ускорениями относительного, переносного и абсолютного движений точки.

Положение точки М по отношению к неподвижной системе характеризуется вектором .

Изменение радиус-вектора или координат x, y, z точки М характеризует относительное движение точки.

Т. о. уравнение относительного движения примет вид:

Теорема о сложении скоростей

Докажем теорему о сложении скоростей для сложного движения точки, состоящего из относительного движения по отношению к подвижной системе отсчета Оxyz и переносного движения вместе с этой системой в случае, когда подвижная система отсчета связана с ТТ, совершающим произвольное движение в пространстве.

Движение свободного ТТ в общем случае состоит из поступательного движения вместе с некоторым полюсом и сферического движения вокруг этого полюса.

Т. о. само переносное движение явл-ся сложным, представляющим собой совокупность поступательного движения подвижной системы вместе с точкой О (полюсом) и сферического движения вокруг этого полюса. Это сферическое движение в каждый момент можно рассмотреть как вращение подвижной системы с угловой скоростью вокруг мгновенной оси Ω_e, проходящей ч/з О. Во все время движения радиусы связаны равенством

По формуле Эйлера

Переносная скорость точки представляет собой скорость точки, связанной с неподвижной системой отсчета и совпадающей в данный момент с движущейся точкой М.

В рассмотренном случае такой точкой явл-ся точка М свободного ТТ. скорость этой точки состоит из скорости полюса О и вращательной скорости точки вокруг мгновенной оси Ω_e.

(6.2.3) выражает теорему о сложении скоростей.

Теорема. Абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей.

В случае поступательного переносного движения скорости всех точек неизменно связанных с подвижной системой отсчета в каждый момент геометрически равны. Тогда переносная скорость

Так как абсолютная скорость точки явл-ся диагональю параллелепипеда, построенного на векторах

Теорема о сложении ускорений.

Для определения абсолют. Ускорения точки в случае непоступательного переносного движения воспользуемся выражением для абсолютной скорости точки.

Продифференцируем (6.3.1), получим:

(6.3.2)

на основании этой формулы получим:

Аналогично

Подставляя эти значения в (6.3.1), получим

Переносное ускорение точки представляет собой ускорение точки, связанной с подвижной системой отсчета и совпадающей в данный момент с движущейся точкой М.

В рассмотренном случае такой точкой является т М свободного ТТ, ускорение которой состоит из ускорения полюса, вращательного ускорения, определенных относительно осей, проходящих через О.

Т. о.

Учитывая это, получим

Равенство (6.3.5) выражает теорему Кориолиса по сложению ускорений в случае непоступательного движения. В случае непоступат-го переносного движения абсолютное ускорение точки равно геометрической сумме переносного, относительного и Кориолисова ускорений.

В случае поступательного переносного движения:

Модуль абсолютного ускорения равен:

15. Общий случай движения ТТ. Разложение движения свободного ТТ на поступательное и сферическое движения. Ур-я движения свободного ТТ.

Положение свободного ТТ в пространстве однозначно определяется положением трех его точек, не лежащих на одной прямой. Соединяя эти точки м/у собой прямыми, получаем треугольник. Т. о. движение ТТ в пространстве можно изучить как движение треугольника, определяющего его положение.

Предпол, что ΔABC определяет положение некоторого тела. Рассмотрим перемещение ΔABC в новое положение A₁B₁C₁.

Осуществим это перемещение как совокупность двух перемещений. Для этого соединим одну из двух вершин, например, А с её новым положением А₁. Затем проведем отрезки BB’ и CC’, равные и параллельные АА₁. Соединив м/у собой прямыми точки А₁,B’,C’, получим Δ-ник А₁B’C’, стороны которого равны и параллельны сторонам ∆-ка ABC как противоположные стороны параллелограмма. ∆ А₁B’C’ представляет собой новое положение Δ ABC после его поступательного перемещения вместе с точкой А, принятой за полюс. Согласно теореме Эйлера-Даламбера для перемещения Δ-ка из положения А₁B’C’ в положение A₁B₁C₁ произведем поворот треугольника на некоторый угол вокруг оси, проходящей через точку А₁, которая не участвует в перемещении.

Т. о. установлено, что всякое перемещение свободного ТТ из одного положения в другое можно осуществить совокупностью двух перемещений : поступательного вместе с точкой, принятой за полюс, и поворота тела вокруг некоторой оси, проходящей ч/з полюс.

На рис а) и б) показано, что результирующее перемещение тела не зависит от последовательности, в которой осуществляются составляющие перемещения.

Перемещение Δ-ка из положения АВС в положение A₁B₁C₁ можно осуществить путем поворота его вокруг оси, проходящей ч/з точку А, до положения АВ’С’ в первую очередь и поступательного перемещения вместе с полюсом А из положения АВ’С’ в положение A₁B₁C₁ во вторую очередь.

Очевидно, что совокупность этих двух перемещений не отображает действительного движения ТТ, а позволяет лишь осуществить перемещение ТТ из 1-го положения во 2-ое.

При действительном движении ТТ составляющие движения этого тела совершаются одновременно, т. е. движение свободного ТТ можно рассмотреть как сложное, состоящее из поступательного вместе с некоторой точкой тела, принятой за полюс, и сферического движения вокруг этого полюса.

Поступательная часть движения ТТ определяется движением полюса О. Обозначим координаты полюса О в неподвижной системе осей декартовых координат через x_O, y_O, z_O, получим уравнения движения.

Сферическое движение ТТ можно определить заданием эйлеровых углов.

Для определения эйлеровых углов проведем три взаимно перпендикулярных оси a,b,c, движущиеся поступательно вместе с точкой О и остающиеся параллельными неподвижным осям x, y,z, а также взаимно перпендикулярные оси ξ, η, ζ, связанные с телом; определив с помощью этих осей эйлеровы углы ψ,θ,φ, напишем три ур-я сферического движения вокруг полюса О.

Т. о. движение свободного ТТ определяется шестью уравнениями, называемыми уравнениями движения свободного ТТ.

16. Теорема о скоростях и ускорениях точек свободного ТТ и ее следствия.

5.2.2 выражает теорему об ускорениях точек свободного ТТ

Теорема. (Теорема Ривальса). Ускорение точек свободного ТТ равно геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенной оси и оси углового ускорения, проходящих через полюс.

Следств. Проекции скоростей точек свободного ТТ на ось, проходящую через эти точки, равны.

Следств. Скорости точек свободного ТТ, расположенных в данный момент на прямой, параллельной мгновенной оси, геометрически равны.

21. Основные теоремы динамики точки. Импульс силы. Теорема об изменении количества движения и момента количества движения

Пусть сила постоянная по модулю и направлению действует на точку за время . Приэтом величину называют импульсной силой.

Эта величина характеризует передачу материальной точке механической энергии В общем случае

Соответственно

; ;

Модуль выражения определяется следующим образом:

В случае действия нескольких сил — импульс равнодействующей нескольких

сил за некоторый промежуток времени равен геометрической сумме импульсов составляющих сил за это же время.

Это же правило имеет место и для проекций.

Количеством движения материальной точки называют вектор, имеющий направление вектора скорости и модуль, равный произведению массы точки т на модуль скорости его движения

Проекции количества движения на оси координат

Предположим, что вектор равнодействующая всех сил, действующих на точку. Запишем дифференциальное уравнение движения

Уравнение (3.18) выражает теорему об изменении количества движения:

Теорема. Производная по времени от количества движения материальной точки геометрически равна равнодействующей сил, приложенных к этой точке.

Из этого уравнения:

(3.19)

Отсюда Если на тело действуют несколько сил, то тогда

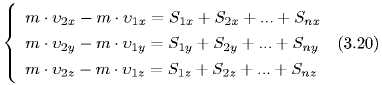
Уравнение (3.20) показывает, что изменение проекции количества движения материальной точки на данную ось за некоторый промежуток времени равно сумме проекции на ту же ось импульсов, приложенных к точке сил за тот же промежуток времени.

— момент силы

Моментом количества движения в точке М относительно точки О называют вектор ,

направленный перпендикулярно плоскости проходящий через и точку О

Проекция момента количества движения относительно осей координат имеют вид

где — координаты движущейся точки М, — проекции скорости точки на осях координат.

Предположим, что движение точки М происходит под действием силы . Проведем из произвольного центра О в точке М радиус-вектор и определим момент силы относительно этого центра.

Определим связь между моментом количества движения и моментом силы . Найдем производную (3.21)

Таким образом,

Если на материальную точку действуют несколько сил

Состояние (3.22) выражает теорему об изменении момента количества движения материальной точки относительно центра:

Теорема. Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна геометрической сумме моментов сил, действующих на точку относительно того же центра.

В проекциях на оси координат эта теорема запишется в виде:

Выражения (3.23) представляют теорему об изменении момента количества движения точки относительно осей координат.

Следствие. Если линия действия равнодействующей приложенных к материальной точке сил все время проходит через некоторый неподвижный центр, то момент количества движения материальной

точки относительно этого центра остается постоянной.

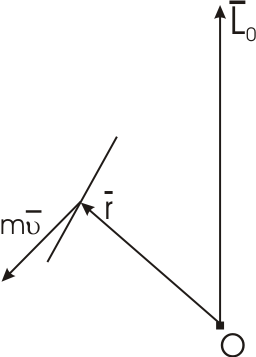
Примером, иллюстрирующим этот случай является движение материальной точки под действием центральной силы.

Центральной силой называется сила, линия действия которой за время движения проходит через некоторый центр, а модуль зависит от расстояния между этим центром и точкой приложения силы.