Mekhanika-6_2013

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИЗУЧЕНИЕ УПРУГИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ

ЛАБОРАТОРНАЯ РАБОТА ПО МЕХАНИКЕ № 6

для студентов 1-го курса физико-технического института, химического факультета и факультета математики и информационных технологий

Уфа РИО БашГУ 2013

1

Печатается по решению кафедры общей физики: протокол № 6 от 24 апреля 2013 г.

Составители: к.ф.-м.н., ст.преп. Заманова Г.И.

2

Лабораторная работа № 6 Изучение упругих характеристик материалов

Приборы и принадлежности: прибор для определения удлинения проволоки, зрительная труба, прибор для определения угла закручивания стержня, осветитель с полупрозрачной миллиметровой шкалой, крутильный маятник, секундомер

Цель работы: 1. Проверка справедливости закона Гука при деформациях растяжения и сдвига. 2. Определение модулей упругости и сдвига.

Краткая теория.

Деформацией называется изменение формы и размеров тела под действием силы. Различают два предельных случая деформации: упругая и пластическая (неупругая). Деформация, исчезающая после прекращения действия силы, называется упругой. Если после прекращения действия внешней силы в теле в некоторой степени сохраняется деформация, то такая деформация называется пластической. Строго говоря, все деформации после прекращения действия внешней силы исчезают не полностью. Однако, если величины остаточных деформаций малы, то во многих случаях ими можно пренебречь. Какой остаточной деформацией можно пренебречь – это зависит от конкретных условий. В некоторых случаях пренебрегают остаточной деформацией, составляющей около 0,1% от максимальной величины деформации, в других случаях этот предел снижают до 0,01%.

В зависимости от того, каким образом приложена внешняя сила, тело деформируется по-разному и соответствующие деформации делятся на следующие типы:

оказывается, что любую упругую деформацию можно свести к двум основным типам: деформация растяжения и деформация сдвига.

Таким образом, под действием внешней силы происходит изменение размеров тела. Следовательно, по величине изменения размеров

длиной 10 мм и 1 м в первом случае деформация весьма заметна, во втором настолько мала, что ею можно пренебречь. Поэтому величину деформации оценивают отношением изменения размеров тела x при деформации к размерам тела до деформации. Это отношение называют относительной деформацией:

При деформации растяжения и сжатия тело изменяет свою длину на l. Знак «+» соответствует растяжению, знак «-» соответствует сжатию. Тогда относительная продольная деформация будет

где l – длина тела до деформации.

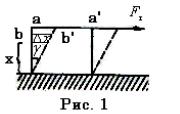
При сдвиге абсолютная величина перемещений слоев различна (рис.1). Возьмем отношение абсолютной величины смещения в слое к расстоянию до слоя от точки 0, которая при деформации остается неподвижной.

Эти отношения одинаковы для всех слоев:

aa 0a bb 0b ... xx tg (3)

Угол , образованный направлениями одной и той же грани в недеформированном теле, называется углом сдвига. При малых деформациях можно принять

xx .

Величину называют относительным сдвигом. Таким образом, для малых деформаций . Возьмем

стержень в виде кругового цилиндра L и радиусом R (рис.2). Допустим, что верхнее сечение стержня закреплено, а к нижнему приложена пара сил, под действием которой радиус нижнего сечения ОА повернется на некоторый угол . Тогда отношение угла закручивания к длине стержня L

3

будет называться относительной деформацией кручения.

Из закона сохранения массы следует, что при растяжении или сжатии должна меняться не только длина тела, но и его поперечный размер. Изменение поперечных размеров тела при его растяжении или сжатии характеризуется соответственно относительным поперечным сжатием или расширением:

где d – поперечный размер тела до деформации, d - абсолютная величина изменения поперечного размера тела.

Абсолютная величина частного от деления относительной поперечной деформации тела на его относительную продольную деформацию называется коэффициентом Пуассона (С.Д.Пуассон (1781 – 1841 гг.) – французский ученый):

d 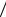L (6)

Коэффициент Пуассона не зависит от размеров тел. Для многих металлов коэффициент Пуассона близок по величине к 0,25 , для материалов типа резины он равен примерно 0,5. Опыт показывает, что тело под действием определенной величины внешней силы деформируется также на определенную величину. Спрашивается, почему деформация тела после достижения определенной величины прекращается, хотя внешняя сила продолжает действовать? Дело в том, что при деформации происходит нарушение равновесия внутренних сил, действующих между атомами, находящимися в узлах кристаллической решетки. В результате в каждом сечении тела появляются отличные от нуля результирующие внутренних сил, направленные против внешней силы. Величина этих сил возрастает до тех пор, пока они не станут равными внешней силе. В момент уравновешивания внешних сил внутренними деформациями тело достигает определенной величины и больше не изменяется. Внутренние силы, возникающие внутри тел при их деформации, называются силами упругости. Согласно 3-му закону Ньютона сила упругости по модулю равна величине внешней силы и противоположна ей по направлению:

Если убрать внешнюю силу F , то упругие силы восстановят первоначальные форму и размеры. Внешняя сила F, действующая на единицу площади поверхности тела S, называется усилием:

Внутренние силы, действующие на единицу площади сечения, проведенного внутри тела,

называются напряжением:

Внешняя сила в общем случае может быть ориентирована как угодно относительно поверхности тела. Но ее всегда можно разложить на составляющие: в направлении нормали и в направлении касательной к поверхности тела в точке приложения силы. При установившейся деформации результирующая внутренних сил, возникших в теле, очевидно, уравновешивает в любом сечении обе составляющие внешней силы, т.е. сама имеет нормальную и касательную составляющие.

Для упругой деформации справедлив закон, установленный в 1675 г. английским физиком Р.Гуком

(1635-1703 гг.) на основе большого числа измерений: величина деформации x пропорциональна действующей силе F. Запишем уравнение этого закона в виде

F=k∆x, (10)

где k – величина , постоянная для данного тела. Очевидно, она зависит от размеров деформируемого тела, поэтому пользуются обычно законом Гука в другой форме, который справедлив даже для каждой точки (элементарного объема) деформированного тела. Для получения искомой формы закона Гука проделаем

4

следующие операции: заменим в выражении (7) F на Fупр, умножим и поделим в выражении (10) левую часть на площадь поперечного сечения S , а правую – на длину тела до деформации l, т.е.

Таким образом, из этого выражения закона Гука следует, что для малых деформаций напряжения,

возникающие в деформированном теле, прямо пропорциональны величине относительной деформации. Это выражение называется законом Гука в дифференциальном виде, т.к. оно справедливо для любой точки деформированного тела. Следовательно, оно может описать и неоднородно деформированные тела. Коэффициент Е называется модулем Юнга (иногда модулем упругости).

Допустим, что =1. Тогда =Е. Учитывая (7), для продольного растяжения стержня можно сказать, что модуль Юнга численно равен усилию, которое вызывает единичное относительное удлинение, т.е. ∆l (абсолютное удлинение) при этом будет равно первоначальной длине стержня. Следует отметить, что столь большие упругие деформации невозможны (кроме резины). Модуль Юнга Е и коэффициент Пуассона µ полностью характеризуют упругие свойства однородного материала.

называется коэффициентом упругости.

Связь между деформацией и напряжением графически изображается так называемой диаграммой напряжений. Для ее построения специальными приборами измеряют деформации и соответствующие им величины внешних сил. Если при измерении обеспечено медленное нарастание деформаций и сил, то можно считать, что измерение производится при установившейся деформации и напряжение в теле равно усилию. На рис.3 приводится диаграмма напряжений для деформаций растяжения металлического образца. Как видно на графике, линейная зависимость ( L ),

установленная Гуком, выполняется лишь на участке ОА (весьма узкий предел изменения деформаций и напряжений). Предельное значение напряжений, при котором еще соблюдается линейная зависимость напряжения от деформации, называется пределом

пропорциональности ( п ) и на графике это ордината точки А.

Строго говоря, не существует определенного значения предела пропорциональности, т.к. возможность обнаружить отступления от линейной зависимости определяется точностью измерения.

При больших степенях деформации линейная зависимость ( L ) уже не сохраняется, но

деформация все еще остается упругой. Т.е., если снять нагрузку с образца, то он вернет свои первоначальные форму и размеры (восстановление размеров произойдет по кривой В-А-О). Предельное напряжение, при котором еще восстанавливаются размеры деформируемого тела, называется пределом

упругости ( У ). Участок АВ очень мал и в инженерных расчетах пределы пропорциональности и

упругости считаются совпадающими.

За пределом упругости в теле возникают деформации, сохраняющиеся и после снятия внешней силы. В этом случае при уменьшении внешней силы восстановление размеров не будет происходить по пути В-А-О, а пойдет по параллельной кривой линии (на рис.3 – пунктирная линия). Отрезок между т.О и пересечением пунктирной линии с осью абсцисс называется остаточной деформацией. Напряжение, при

котором появляется заметная остаточная деформация (около 0,2%), называют пределом текучести ( ).

На кривой ей соответствует т.С. В области СД деформация возрастает без увеличения нагрузки, тело как бы «течет». Эта область называется областью пластических деформаций и в основе ковки, чеканки, прессовании, волочении, проката материалов лежит пластическая деформация.

Материалы, для которых область текучести значительна, называются вязкими (свинец, глина, пластилин и т.д.), если эта область практически отсутствует - хрупкими (кирпич, бетон, фарфор, стекло и т.д.). Однако, при изменении внешних условий, могут меняться и свойства деформируемого тела (свинец при комнатной температуре пластичен, а при температуре жидкого азота (77 К) становится хрупким.

При дальнейшем растяжении (за т.Д) тело вновь оказывает сопротивление деформации. Максимальное напряжение, (т.Е), возникающее в теле до разрушения, называется пределом прочности.

5

При напряжении, превышающем предел прочности, в одном из сечений тела образуется сужение (шейка) и далее деформация сосредотачивается в этом сечении и материал разрушается.

Рассмотрим закон Гука для деформации сдвига. Слои тела будут сдвигаться друг относительно друга когда нижняя его поверхность закреплена, а на

верхнюю приложена сила F (рис.1). Отношение этой

силы к площади поверхности S,на которую она действует, называется касательным напряжением

Тогда для деформации сдвига закон Гука будет иметь вид:

где постоянная величина G называется модулем сдвига изависит от материала деформируемого тела, -

относительная деформация сдвига.

Для деформации кручения закон Гука имеет

вид

где М – вращающий момент относительно продольной оси стержня, С – постоянная для данного стержня величина, называемая модулем кручения и - угол закручивания нижнего торца стержня. В отличие от модулей Юнга Е, сдвига С и коэффициента Пуассона ,

модуль кручения зависит не только от материала, но и от геометрических размеров стержня. Эта зависимость дается формулой

где r - радиус стержня, l – длина стержня , G – модуль сдвига. Связь между C и G объясняется тем, что кручение можно себе представить как сдвигающиеся друг относительно друга слои, из которых сложен стержень.

6

Упражнение 1. Проверка закона Гука и определение модуля Юнга из растяжения.

Из формулы (11) следует, что для проверки закона Гука и определения модуля Юнга необходимо знать величину абсолютного удлинения Δl, которое обычно бывает настолько малым, что для его измерения с достаточной точностью приходится использовать соответствующие устройства. В данном упражнении используется прибор, состоящий из двух кронштейнов А и Б (рис.4), которые расположены один над другим и служат для укрепления проволоки из исследуемого материала. При нагрузке, осуществляемой грузами РР, проволока удлиняется. Для измерения удлинения Δl служит следующее устройство. Стержень r, несущий зеркальце M и опирающийся на диск d, может вращаться вокруг оси 0. При удлинении проволоки на Δl

где b – длина стерженька r. Луч света, отраженный от зеркальца M, падает на шкалу S. При удлинении проволоки «зайчик» будет смещаться по шкале. Из геометрической оптики известно, что при повороте зеркальца на угол α отраженный луч поворачивается на угол 2α и поэтому можно записать

где Δn – расстояние, на которое сместился «зайчик» по шкале, D – расстояние от зеркальца до шкалы.

Сопоставляя формулы (17)-(19), получим выражение, связывающее удлинение проволоки Δl и смещение

Возьмем постоянную прибора k = b/2D , тогда равенство (20) примет окончательный вид

Δl = k ∙ Δn .

Нижний кронштейн В имеет арретир f, которым пользуются при работе. При нагружении проволоки винт «е» арретира должен быть завернут, а при измерениях – вывернут, что освобождает проволоку от арретира. Грузы, необходимые для нагрузки проволоки, берут с особого подвеса К, укрепленного на верхнем кронштейне; при уменьшении нагрузки грузики укладывают на подвес, а при увеличении нагрузки их берут с подвеса. Этим достигается постоянство прогиба верхнего кронштейна. Нагружать проволоку и снимать нагрузку нужно всегда при поднятом арретире.

Измерения.

1.Опустите арретир. Включите осветительную лампу Л и добейтесь, чтобы свет падал на зеркальце М, а «зайчик» - на шкалу S. Запишите «нулевое» положение «зайчика» - n.

2.Нагрузите проволоку последовательно одним, двумя,…, пятью грузами, снимая их с подвеса. Запишите смещения Δni = ni – nо «зайчика», соответствующие каждой нагрузке. Проделайте 5 серий подобных измерений и занесите данные в таблицу. Найдите среднее арифметическое значение смещений для каждой нагрузки из 5 измерений.

3.Постройте график зависимости деформации от нагрузки, откладывая по оси абсцисс нагрузку, а по оси ординат – среднее значение удлинения li . Убедитесь, выполняется закон Гука или нет.

4.Найдите модуль Юнга для одной нагрузки. Из (2), (9), (11), (20) можно вывести выражение для модуля Юнга в виде

где значения lо, D, R и b приведены на установке, m равна массе груза при котором определяется модуль, g = 9,81 м/с2 . Найдите абсолютную ΔE и относительную εЕ погрешности. Сравните полученное значение Е с табличным.

Упражнение 2. Определение модуля сдвига динамическим методом.

Метод основан на зависимости периода крутильных колебаний маятника, подвешенного на исследуемой проволоке, от упругих свойств материала проволоки. Для определения модуля сдвига из

7

крутильных колебаний служит прибор , состоящий из кронштейна, в котором зажата проволока из исследуемого материала (рис.5). К нижнему концу проволоки прикреплена горизонтальная рейка, нагруженная одинаковыми грузами m1, m2 (m1= m2=m). Грузы расположены на рейке симметрично и могут устанавливаться на расстояниях d1 и d2 от оси вращения, проходящей через середину рейки. Если повернуть систему на малый угол и предоставить сомой себе, то она начнет совершать крутильные колебания. Период этих колебаний можно найти из следующих соображений. Т.к. тело при крутильных колебаниях совершает вращательное движение, то к нему можно применить основной закон вращательного движения

где M – вращающий момент сил относительно оси, совпадающей с исследуемой проволокой, I – момент инерции тела относительно той же оси; β = φ – угловое ускорение , равное 2-й производной угла поворота. Пользуясь выражением 15, перепишем уравнение (22) в виде

Знак « - » показывает, что вращающий момент направлен так, чтобы уменьшить угловое смещение φ. Уравнение (23) можно представить в виде

Уравнение (26) называется дифференциальным уравнением гармонических колебаний (ωo - собственная циклическая частота гармонических колебаний). Таким образом, рейка с грузиками, подвешенная на исследуемой проволоке, совершает гармонические колебания. Зная связь периода гармонических колебаний с их циклической частотой (ωo = 2π/T) и , учитывая (25), получим для периода колебаний формулу

Из (27) можно было бы найти С, если был бы известен I. Вычисление I маятника довольно трудная задача. Чтобы обойти эту трудность, поступают следующим образом. Определяют период колебаний маятника при двух различных положениях грузов m. В первом случае общий момент инерции крутильного маятника будет

I1= Iо+2md1²,

где 2md1² - момент инерции двух грузов относительно оси вращения, Iо- момент инерции остальных частей колеблющейся системы. Если грузы поместить на расстоянии d2 от оси , то аналогично имеем

I2= Iо+2md2².

Тогда формулы периодов колебаний для этих двух случаев будут иметь вид

T1=2 Io 2md12 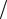C

Т2=2 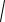Io 2md22 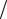C .

Возведя последние уравнения в квадрат и вычитая затем почленно одно из другого, решим полученное выражение относительно С. Получаем

Измерения

8

1. Повернуть крутильный маятник на малый угол от положения равновесия для d1. Определить время 10 полных колебаний t1. Провести подобные измерения 5 раз. Найти среднее значение времени < t1>. Определить среднее значение периода колебаний < T1>.

2.Провести аналогичные измерения при другом положении грузов (при d2 ). Найти среднее значение периода < T2>.

3.Подставив значения < T1> и < T2>, вычислить значение модуля сдвига G . Определить абсолютную G и относительную εG погрешности. Сравнить вычисленное значение G с табличным.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что называется деформацией тела?

2.Какие деформации называются упругими, пластическими?

3.Сформулируйте закон Гука.

4.Перечислите типы деформаций и объясните при каких условиях они возникают.

5.Что называется абсолютной, относительной деформацией (при растяжении, сдвиге, кручении).

6.Запишите закон Гука: для деформации растяжения, сдвига, кручения.

7.Что характеризуют модули упругости и сдвига?

8.Дайте характеристику коэффициента Пуассона.

9.Нарисуйте график зависимости σ=f(ε) и объясните его.

10.Что называется остаточной деформацией, пределом пропорциональности, пределом упругости, пределом прочности?

11.Объясните назначение осветителя и зеркальца в упр.1.

12.В чем состоит сущность статического и динамического методов определения модуля сдвига?

13.Выведите формулу для периода колебаний крутильного маятника.

14.Погрешности каких величин вносят основной вклад в погрешности модулей упругости и сдвига?

15.Каким образом можно увеличить точность методов, описанных в упр.1,2?

16.Что дает сравнение измеренных значений модулей с табличными?

ЛИТЕРАТУРА

1.Стрелков С.П. Механика. С.-П., М., Кр-р, 2005, с.282-314.

2.Хайкин С.Э. Физические основы механики. С.-П., М., Кр-р, 2008, §§35-38, с.162-174.

3.Трофимова Т.И. Курс физики. М., 2004, §21, с.43-46.

ПРИЛОЖЕНИЕ

9