
Metod-zaochn
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЗАДАЧИ ПО ОБЩЕЙ ФИЗИКЕ (механика, молекулярная физика)
Методические указания по решению задач для студентов 1 курса заочного отделения физико-технического института Башгосуниверситета специальности «ФТОС»
Уфа РИО БашГУ
2011
Печатается по решению кафедры общей физики БашГУ (протокол № от .).
Ответственные за выпуск:
канд. физ.-мат. наук, доц. В.Н. Назаров канд. Физ.-мат. наук. доц. Ш.З. Измайлов
МЕХАНИКА
Механика – это раздел физики, который изучает механическую форму движении материи.
Механика подразделяется на ньютоновскую механику, релятивистскую механику и квантовую механику. Ньютоновская механика изучает механическое движение макроскопических тел, движущихся со скоростями, много меньшими скорости света в вакууме. Релятивистская механика изучает механическое движение макроскопических тел, движущихся со скоростями, сравнимыми со скоростью света. Квантовая механика изучает механическое движение микроскопических тел (отдельных атомов и элементарных частиц).
Механика состоит из трех разделов: кинематика, динамика и статика. Кинематика изучает движение тел (изменение движения) без учета
причин их вызывающих.
Динамика изучает движение как результат взаимодействия тел. Статика изучает условия равновесия тел под воздействием сил.
Кинематика поступательного и вращательного движения
Материальная точка – это модель реального тела, размерами и формой которого в данной задачи пренебрегают.
Движение материальной точки всегда рассматривается в системе отсчета – это совокупность неподвижных относительно друг друга тел, по отношению к которым рассматривается движение, и отсчитывающих время 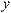



















часов. Положение материальной точки в пространстве можно задать двумя способами: векторный и координатный. Радиус-вектором материальной точки А относительно начала О называется вектор, проведенный из начала О в
точку А. Если ввести орты координатных осей (единичные векторы i , j ,
k , модуль которых равен 1), то можно
3

записать связь между радиус-вектором и декартовыми координатами материальной точки:
rr = xi + yj + zk .
В кинематике знать движение материальной точки означает: знать какой функцией времени является ее радиус-вектор r = r (t) либо декарто-
вы координаты x = x(t) , y = y(t) , z = z(t) .
Если точка при своем движении в пространстве переместилась из положения 1 в положение 2 за время ∆t = t2 −t1 , то вектор
перемещения ∆r есть вектор, проведенный из начально-
го положения в конечное:
∆r = r2 − r1 .
Траектория – это совокупность точек пространства, в которых побывала материальная точка при своем движении. Пройденным путем ∆S называется расстояние, отсчитанное по траектории.
Скорость и ускорение материальной точки
Средний вектор скорости перемещения точки в пространстве за время ∆t определяется отношением вектора перемещения ∆r к промежутку времени, за который это перемещение произошло:
< vr > |
∆t |
= |
∆r |
= |
r2 − r1 |
. |
||
∆t |
|
|||||||
|
|
|
t |
2 |
−t |
|||
|
|
|
|
|
|
1 |
|
|
Средняя скорость движения по траектории определяется отношени-
ем пройденного пути ∆S за время ∆t |
к этому времени: |
|||||||
< v > |
∆t |
= |
∆S |
= |
S2 − S1 |
. |
||
∆t |
|
|||||||
|
|
|
t |
2 |
−t |
|||
|
|
|
|
|
|
1 |
|
|
Мгновенный вектор скорости равен первой производной радиусвектора точки по времени:
vr = drdt = rr& .
Модуль мгновенной скорости равен отношению бесконечно малого перемещения dS к бесконечно малому времени dt , за которое это перемещение произошло:
v = dSdt = S& .
4
В декартовой системе координат связь между вектором скорости и его компонентами имеет следующий вид:
vr = vxir + vy rj + vz k , где vx = dx |
, |
vy = dy |
, |
vz = dz . |
dt |
|
dt |
|
dt |
Модуль скорости можно определить через его компоненты: v =  vx2 + v2y + vz2 .
vx2 + v2y + vz2 .
Средний вектор ускорения за время ∆t равен отношению приращения вектора скорости за время ∆t к этому времени:
< ar > |
∆t |
= |
∆v |
= v2 −v1 . |
||
|
|
∆t |
t |
2 |
−t |
|
|
|
|
|
|
1 |
|
Мгновенное ускорение равно первой производной вектора скорости или второй производной радиус-вектора по времени:
ar = dvdt = vr& = &rr&.
Связь между вектором ускорения и его компонентами в декартовой системе координат можно записать в следующем виде:
ar = axir + ay rj + az k ,
где
ax = |
dv |
x |
= |
d 2 x |
, ay = |
dvy |
= |
d 2 y |
, az = |
dv |
z |
= |
d 2 z |
. |
||
dt |
dt 2 |
dt |
dt |
2 |
dt |
dt 2 |
||||||||||
|
|
|
|
|
|
|
||||||||||
Полное ускорение состоит из двух взаимно перпендикулярных векторов: ускорения, которое характеризует быстроту изменения модуля скоро-
сти и называемое тангенциальным или касательным ускорением arτ = dvdt rτ
и ускорения, которое характеризует быстроту изменения направления век-
тора скорости и называемое нормальным или центростремительным
arn = v2 |
nr . |
R |
|
Здесь τ и n – орты, направленные по касательной вдоль траектории и по главной нормали к центру кривизны траектории соответственно; R – радиус кривизны траектории.
Тогда вектор ускорения через нормальные и тангенциальные составляющие можно записать в виде:
5

a = aττ + ann .
Возведя в квадрат, получим абсолютное значение полного ускорения:
a = |
a |
2 |
+ a |
2 |
= |
dv 2 |
v2 |
|
2 |
||
τ |
n |
|
|
+ |
|
. |
|||||
|
|
|
|
dt |
|
R |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Уравнения равномерного и равноускоренного движений
В случае равномерного прямолинейного движения материальной точки ( v = const ) функция r (t) имеет вид:
r (t) = r0 + vt ,
а для равнопеременного движения ( a = const ):
rr(t) = rr |
+ vr |
t + |
art 2 |
. |
|
||||
0 |
0 |
2 |
|
|
|
|
|
||
Здесь r0 – начальное положение точки, rr0 = rr(t) t =0 = rr(0) ; v0 – на-
чальная скорость.
При решении задач часто удобно записывать функцию r (t) непосред-
ственно в проекциях на оси координат. Тогда при постоянном ускорении a функцию r (t) можно представить в виде двух уравнений:
|
a |
t 2 |
|
|
ayt 2 |
|
|
x(t) = x0 + v0 xt + |
x |
|
, |
y(t) = y0 + v0 yt + |
|
. |
|
2 |
2 |
||||||
|
|
|
|
||||
В частности, при движении материальной точки под действием силы тяжести удобно выбрать ось y вертикально вверх. В этом случае вектор
ускорения имеет лишь одну проекцию, отличную от нуля ( ax = 0 , ay = −g ,
где g = 9,81 м/с2 ): |
|
|
|
|
|
x(t) = x0 + v0 xt = x0 + v0 cos α t, |
|
|
|||
y(t) = y0 + v0 y y − |
gt 2 |
= y0 + v0 sin α t − |
gt 2 |
, |
|
2 |
2 |
||||
|
|
|
|||
где α – угол, образованный вектором начальной скорости v0 с горизонтом.
Часто удобно поместить начало координат в начальной точке траектории
( x0 = y0 = 0 ).
6
Движение точки по окружности
Средняя угловая скорость за время ∆t |
равна отношению угла поворо- |
||||||
та радиус-вектора точки за время ∆t к этому времени ∆t : |
|||||||
< ω > |
∆t |
= ∆ϕ |
= ϕ2 −ϕ1 . |
||||
|
∆t |
|
t |
2 |
−t |
||
|
|
|
|
|
|
1 |
|
Мгновенная угловая скорость равна первой производной угла поворо- |
|||||||
та по времени: |
|
|
dϕ |
|
|
|
|
|
|
|
|
& |
|
|
|
|
ω = dt |
= ϕ . |
|
||||
Среднее угловое ускорение за время ∆t |
равно отношению приращения |
||||||
угловой скорости за время ∆t к этому времени: |
|||||||
< β >= |
∆ω = ω2 −ω1 . |
||||||
|
|
∆t |
t |
2 |
−t |
||
|
|
|
|
|
|
1 |
|
Мгновенное угловое ускорение равно первой производной угловой скорости или второй производной угла поворота по времени:
β = ddtω = ω& = ϕ&& .
Связь между линейной и угловой скоростями материальной точки: v = Rω ,
где R – радиус окружности.
Связь между линейным и угловым ускорениями материальной точки: aτ = Rβ.
Бесконечно малое угловое перемещение dϕ материальной точки яв-
ляется вектором. Поэтому угловая скорость является векторной величиной:
ωr = ddtϕ ,
а направление вектора ω определяется по правилу правого винта.
Вектор линейной скорости материальной точки выражается через вектор угловой скорости через векторное произведение:
v =[ω, r ] .
Угловое ускорение также является векторной величиной:
βr = ddtω .
При движении точки по окружности вектор ω меняется лишь по модулю, а по направлению совпадает с неизменной осью вращения.
7
Задача 1.1. Радиус-вектор точки изменяется со временем по закону rr = 2t 2i +tj + k (м). Найти скорость vr и ускорение a точки, модуль ско-
рости v в момент t = 2 с , а также приближенное значение пути S , пройденного точкой за 10-ю секунду движения, и среднюю скорость прохождения этого пути S .
Дано: |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
rr = 2t 2ir +trj + k (м) |
|
Вектор скорости |
v есть первая производная |
||||||||||||||
|
|||||||||||||||||
t = 2 с |
|
радиус-вектора по времени: |
|
|
|
r |
|
||||||||||
|
|
drr |
|
|
|
r |
|
r |
|
|
|
|
|||||
|
|
vr = |
= |
d (2t 2i ) |
+ |
d (tj ) |
+ |
dk |
= 4tir |
+ rj . |
|||||||
|
|
|
|
|
dt |
|
|
||||||||||
vr −? |
|
|
dt |
dt |
|
|
|
dt |
|
||||||||
|
Отсюда видно, что вектор скорости имеет только |
||||||||||||||||
a −? |
|
две компоненты: |
vx и vy . |
|
|
|
|
|
|
||||||||
v −? |
|
Вектор ускорения |
a есть первая производная |
||||||||||||||
S −? |
|
||||||||||||||||
|
от вектора скорости по времени: |
|
|||||||||||||||
< v > −? |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ar = |
dv |
= |
d (4ti ) |
+ |
dj |
= 4ir . |
|
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dt |
dt |
|
dt |
|
|||||||
Получается, что вектор ускорения имеет только одну компоненту, не зависящую от времени ax = 4 м/с2 , значит, движение вдоль оси x является равноускоренным, а вдоль оси y – равномерным.
Найдем теперь модуль скорости. Так как vz = 0 , то
v =  vx2 + v2y =
vx2 + v2y =  (4t)2 +1
(4t)2 +1
и в момент времени t = 2 с
v = (4 2)2 +1 ≈ 8 м/с .
Для нахождения пути S , пройденного точкой за 10-ю секунду движения, можно считать его приближенно равным перемещению, так как промежуток времени достаточно мал. Тогда найдем перемещение r9 за время
t9 = 9 c и r10 за время t10 =10 c и возьмем их разность. Учитывая
| rr(t) |= x2 + y2 + z2 = (2t 2 )2 +t 2 +1 ,
получим
r = (2 92 )2 |
+92 +1 ≈162,25 м , |
r = 2002 |
+102 |
+1 ≈ 200,25 м , |
9 |
|
10 |
|
|
тогда путь за 10-ю секунду движения
8
S = r10 − r9 = 200,25 −162,25 = 38 м.
Среднюю скорость прохождения пути S нетрудно найти:
< v >= |
r10 − r9 |
= |
|
38 |
= 38 |
м . |
||
|
10 −9 |
|||||||
|
t |
−t |
9 |
|
|
с |
||
10 |
|
|
|
|
|
|
||
Следует заметить, что в строгом смысле для нахождения пути S надо сначала установить зависимость длины пути от времени. Тогда можем найти точно путь за 9 и за 10 секунд. Функция v(t) нам известна, тогда:
S(t) = ∫v(t)dt = ∫ 16t 2 +1 dt = 12 t
16t 2 +1 dt = 12 t  16t 2 +1 + 18 arcsh(4t) .
16t 2 +1 + 18 arcsh(4t) .
Откуда найдем требуемый путь:
S = 102  16 102 +1 + 18 arcsh(4 10) − 92
16 102 +1 + 18 arcsh(4 10) − 92  16 92 +1 − 18 arcsh(4 9) =
16 92 +1 − 18 arcsh(4 9) =
= 200,61−162.60 ≈ 38 м .
Получаем такой же результат.
Ответ: |
r |
r |
|
r |
, |
r |
|
r |
, |
|
|
v |
= 4t i |
+ j |
a |
= 4 i |
|
||||||
|
|
|
|
|
|
|
|
|
, |
|
. |
|
|
|
|
|
|
||||||
|
v ≈ 8 м/c |
, |
|
S ≈ 38 м |
< v >≈ 38 м/c |
||||||
Задача 1.2. Тело падает с высоты h без начальной скорости. Какой путь пройдет тело за n -ую секунду своего падения, за последнюю секунду? За какое время тело пройдет n -ый метр своего пути, последний метр?
Дано: h
n
v0 = 0
hn −?
hпосл −?
∆tn −?
∆tпосл −?
Решение:
На примере этой задачи продемонстрируем, как удачно выбранная система координат может значительно упростить решение. Выберем систему координат, начало которой совпадает с начальным положением тела, а ось координат направлена вертикально вниз (см. рис.).
Вэтой системе координат
уравнение движения имеет вид:
y = |
gt 2 |
. |
|
2 |
|||
|
|
9

В момент времени t = (n −1)τ тело находится в точке A , |
а в момент |
|||||||
времени t = nτ – в точке B , где τ =1 c , |
n – число секунд падения до точки |
|||||||
B . Координаты точек A и B соответственно равны: |
|
|||||||
yA = |
g(n −1) |
2 τ2 |
yB = |
gn2τ2 |
|
|
||
|
|
|
, |
|
. |
|
||
|
2 |
|
2 |
|
||||
|
|
|
|
|
|
|
||
Решая совместно два |
последних |
уравнения |
с учетом |
того, что |
||||
hn = yB − yA , имеем: |
|
|
|
|
|
|
|
|
hn = g2τ2 (2n −1).
В момент времени, когда тело достигло Земли, t = nпослτ , yB = h :
|
gn2 |
|
τ2 |
|
h = |
посл |
|
. |
|
|
|
|||
|
|
2 |
|
|
Тогда путь, пройденный телом за последнюю секунду:
h |
= |
gτ |
2 |
2h |
|
|
|
|
|
− τ . |
|||
посл |
|
2 |
|
|
g |
|
|
|
|
|
|
||
Для нахождения времени ∆tn = tB′ −tA′ |
прохождения n -го метра сво- |
|||||
его пути, введем координаты начала и конца этого метра: yA′ = (n −1)l , yB′ = nl , где l =1 м . Тогда можно написать:
(n −1)l = |
gtA2 ′ |
, |
nl = |
gtB2 ′ |
. |
|
|
||||
|
2 |
|
2 |
|
|
Решая совместно два последних уравнения: |
|||||
∆tn = |
2l ( |
n − n −1). |
|||
|
g |
|
|
|
|
Когда тело достигло Земли nl = h , тогда время прохождения послед- |
|||||
него метра: |
2 ( |
|
h − h −l ). |
||
∆tпосл = |
|
||||
|
g |
|
|
|
|
Можно выбрать другую систему координат, связанную с Землей: начало координат в точке падения, ось координат направлена вертикально вверх. Тогда уравнение движения примет вид:
y = h − |
gt |
2 |
. |
2 |
|
||
|
|
|
10
Используя другие начальные ( y0 = h ) и конечные ( y = 0 ) условия,
получим те же самые ответы.
Можно выбрать систему координат и другим способом: с началом в точке бросания тела и осью, направленной вверх. Несложно проверить, что решение соответствующих уравнений приведут к тем же результатам.
|
|
gτ |
2 |
|
|
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
Ответ: |
h = |
|
(2n −1) |
, |
τ =1 c ; |
|
h |
= |
gτ |
2 |
− τ |
, |
|
|||||||
|
|
|
|
|||||||||||||||||
n |
2 |
|
|
|
|
посл |
|
|
|
g |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
2l ( |
|
|
n −1) |
|
, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∆tn = |
|
n − |
|
|
l =1 м ; |
|
∆tпосл = |
2 ( |
h − h −l ) |
. |
|||||||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
Задача 1.3. |
|
Снаряд вылетает со скоростью |
v0 |
из ствола орудия, |
||||||||||||||||
стоящего у подножия горы, поверхность которой наклонена под углом β к горизонту. Каким должен быть угол α0 стрельбы по отношению к горизон-
ту, чтобы имело место максимальная дальность полета снаряда. Найти также расстояние L вдоль горизонта, куда попал снаряд при таком выстреле.
Дано: |
Решение: |
|
|
|
|
|
|
|
|
|
|
|
v0 |
Выберем |
|
систему |
|||||||||
β |
координат, начало кото- |
|||||||||||
|
рой находится у подно- |
|||||||||||
|
жия горы (см. рис.). |
|
|
|
|
|
|
|
|
|
||
α0 −? |
Запишем |
уравнения |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
L −? |
движения снаряда |
вдоль |
|
|
||||||||
|
||||||||||||
|
||||||||||||
|
|
|||||||||||
|
координатных осей: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
x = v0 cos α t , |
|
|
|
|
|
|
|
|
|
||
|
y = v0 sin α t − |
gt |
2 |
. |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
x = x(t) , y = y(t) являются уравне- |
|||||||||
Заметим, что система уравнений |
|
|||||||||||
ниями движения снаряда в параметрическом виде.
Исключая неизвестное время t , приведем уравнение движения к виду:
y = tg α x − |
gx2 |
|
. |
|
2v02 cos2 |
α |
|||
|
|
11
Уравнение такого вида y = y(x) является уравнением движения в ка-
ноническом виде.
Для прямой OA , где A – точка приземления снаряда, можно записать уравнение y = tg β x . Приравнивая правые части двух последних уравне-
ний, получим:
x = (tg α − tg β) |
2v02 |
cos2 α = |
v02 |
|
(sin 2α − 2 cos2 |
α tg β). |
||||||
|
g |
g |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Наибольшую дальность полета снаряда найдем из условия |
||||||||||||
|
|
|
|
|
|
|
dx |
= 0 , |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
откуда находим: |
|
|
|
|
|
dα |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
dx |
= |
v02 |
(2 cos 2α0 + 2 sin 2α0 tg β)= 0 . |
||||||||
|
dα |
|
||||||||||
|
|
g |
|
|
|
|
|
|
|
|||
С учетом того, что ctg 2α0 = −tg β и, следовательно, 2α0 = π/ 2 +β , имеем:
|
|
1 |
π |
|
||
α0 |
= |
|
|
|
+β . |
|
2 |
2 |
|||||
|
|
|
|
|||
Таким образом, наибольшая дальность полета снаряда будет иметь место при угле бросания, равном сумме 45° и половине угла откоса OA .
Подставляя в выражение для x значение угла α0 , получим максимальное расстояние, куда может попасть снаряд:
L =
|
|
|
1 |
π |
|
|
||
Ответ: |
α0 |
= |
|
|
|
+β |
, |
|
2 |
2 |
|||||||
|
|
|
|
|
|
|||
v02 |
|
(1 −sin β). |
||||
g cos β |
||||||
|
|
|
||||
|
|
v2 |
(1 −sin β) |
|
||
|
|
|
||||
L = |
|
|
0 |
. |
||
g cos β |
||||||
|
|
|
||||
Задача 1.4. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота ϕ по закону
ω = ω0 − kϕ , где ω0 и k – положительные постоянные. В момент времени t = 0 угол ϕ = 0 . Найти зависимости от времени: а) угла поворота; б) угловой скорости.
12
Дано:
ω = ω0 − kϕ
ω0 = const > 0 k = const > 0 t = 0 , ϕ = 0
ϕ(t) −? ω(t) −?
Решение:
Используя определение угловой скорости:
ω = ddtϕ ,
получим линейное дифференциальное уравнение первого порядка относительно угла поворота ϕ :
ddtϕ = ω0 − kϕ.
Разделяя переменные, получим:
dϕ |
= dt . |
|
ω − kϕ |
||
|
||
0 |
|
Интегрируем обе части полученного выражения с учетом начальных условий задачи. Угол поворота меняется от 0 до ϕ , а время от 0 до t :
ϕ |
dϕ |
= ∫t |
|
|
∫ |
dt . |
|||
ω − kϕ |
||||
0 |
0 |
0 |
|
|
|
|
После интегрирования имеем:
ln |
ω0 |
= t , |
|
ω − kϕ |
|||
|
|
||
|
0 |
|
откуда получаем искомую зависимость угла поворота от времени:
ϕ(t) = ωk0 (1 −exp(−kt)).
Взяв от полученного выражения первую производную по времени, получим зависимость угловой скорости от времени:
ω(t) = dϕdt(t) = ωk0 dtd (1 −exp(−kt))= ω0 exp(−kt) .
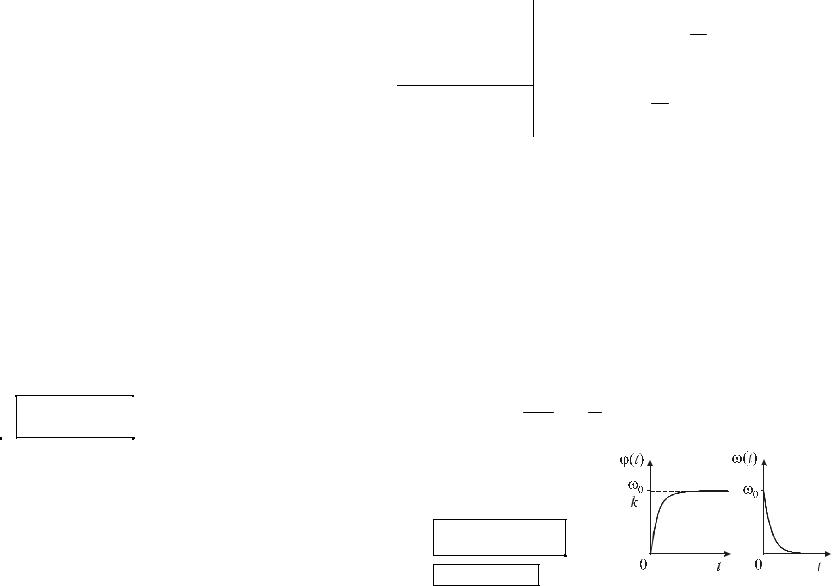
Графический вид найденных функций ϕ(t) и ω(t) пред-
ставлен на рисунке.
Ответ:
ϕ(t) = ωk0 (1 −exp(−kt)) ,
ω(t) = ω0 exp(−kt) .
13

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1.5. Зависимость пройденного телом пути от времени задается уравнением S = 2 +5t +t 2 + 0,3t3 (м). Определить время после начала
движения, через которое ускорение a тела будет равно 20 м/c2 , а также среднюю скорость < v > и среднее ускорение < a > тела за этот промежуток времени.
Задача 1.6. Автомобиль проехал первую половину пути со скоростью v1 = 40 км/ч , а вторую – со скоростью v2 = 60 км/ч . Определить среднюю скорость автомобиля на всем пройденном пути.
Задача 1.7. Первую половину времени своего движения автомобиль перемещался со скоростью v1 = 40 км/ч , а вторую половину – со ско-
ростью v2 = 60 км/ч . Найти среднюю скорость за все время движения автомобиля.
Задача 1.8. Найти скорость v относительно берега лодки, идущей по течению, против течения и под углом α = 90° к направлению течения. Скорость течения реки u =1 м/c , скорость лодки относительно воды v0 = 2 м/c .
Задача 1.9. Лодка движется перпендикулярно к берегу со скоростью v = 7,2 км/ч. Течение относит ее вниз на расстояние l =150 м . Найти скорость u течения реки и время t , затраченное на переправу. Ширина реки L = 0,5 км.
Задача 1.10. Лодка перемещается относительно воды в реке со скоростью v0 = 2 м/c под углом α = 60° к течению, скорость которого
u =1 м/c . Определить скорость v лодки относительно берега, ее направление по отношению к течению и перемещение к моменту времени t = 30 c .
Задача 1.11. С аэростата, находящегося на высоте h = 300 м, упал камень. Через какое время t камень достигнет Земли, если: а) аэростат поднимается со скоростью v = 5 м/c ; б) аэростат опускается со скоростью v = 5 м/c ; в) аэростат неподвижен.
14
Задача 1.12. Свободно падающее тело за последнюю секунду прошло 1/ 3 своего пути. Сколько времени и с какой высоты падало тело?
Задача 1.13. Небольшое тело брошено под углом α к горизонту с начальной скоростью v0 . Пренебрегая сопротивлением воздуха, найти
дальность полета L , наибольшую высоту подъема H , время подъема до максимальной точки и время полета τ, уравнение траектории тела.
Задача 1.14. Чему равно отношение максимальных высот поднятия тел, брошенных под одним и тем же углом к горизонту с начальными скоростями v0 и 2v0 , над первоначальным уровнем?
Задача 1.15. На высоте h горизонтально с постоянной скоростью летит самолет. С земли производится выстрел из орудия, причем скорость снаряда v0 в момент выстрела направлена на самолет под углом α к гори-
зонту. С какой скоростью u летел самолет, если снаряд поразил цель?
Задача 1.16. Шарик падает с нулевой начальной скоростью на гладкую горизонтальную поверхность, образующую с горизонтом угол α .
Пролетев расстояние h , он упруго отскакивает от плоскости. Определить расстояние между точками первого и второго ударов.
Задача 1.17. Тяжелая горизонтальная плита движется вверх с постоянной скоростью u . Легкий шарик начинает свободно падать и, пролетев расстояние h , сталкивается упруго с плитой. Определить время между двумя последовательными ударами шарика о плиту.
Задача 1.18. Каковы линейная и угловая скорости движения точек земной поверхности на широте Уфы ( ϕ = 55° ) при суточном вращении
Земли? Радиус Земли 6400 км.
Задача 1.19. Твердое тело вращается вокруг неподвижной оси по закону ϕ = 6t − 2t3 (рад). Найти: а) средние значения угловой скорости и
углового ускорения за промежуток времени от t = 0 до остановки; б) угловое ускорение в момент остановки тела.
15

Задача 1.20. Диск радиусом R =10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени
задается уравнением ϕ = 8 + 2t +5t2 +t3 (рад). Определить для точек обода
колеса к концу первой секунды после начала движения: а) угловую скорость ω; б) линейную скорость v ; в) тангенциальное aτ и нормальное an
ускорение; г) полное ускорение a ; д) угол, составляемый вектором полного ускорения с радиусом колеса, проведенным через соответствующую точку обода.
Задача 1.21. Колесо радиусом R равномерно катится без скольжения по горизонтальному пути со скоростью v . Найти скорости точек 1, 2 и 3, выразив их через орты координатных осей. Найти также координаты xA и yA произвольной точки A на ободе колеса как
функции времени t или угла поворота колеса ϕ . В
начальный момент xA = 0 , yA = 0 , ϕ = 0 . По най-
денным выражениям для xA и yA построить график
траектории точки на ободе колеса.
Указание. Движение точек обода колеса можно рассматривать как результат сложения двух движений: поступательного движения со скоростью v оси колеса и вращения вокруг этой оси. Для этих точек при отсутствии скольжения колеса модули векторов скорости поступательного движения и линейной скорости, обусловленной вращением, равны друг другу.
Задача 1.22. Автомобиль с колесами радиусом R движется со скоростью v по горизонтальной дороге, причем v2 > Rg , где g – ускоре-
ние свободного падения. На какую максимальную высоту h может быть заброшена вверх грязь, срывающаяся с колес автомобиля? Указать положение той точки на покрышке колеса, с которой при данной скорости движения автомобиля грязь будет забрасываться выше всего. Сопротивление воздуха движению отброшенного вверх грязи не учитывать.
Задача 1.23. Якорь электродвигателя, вращавшийся с частотой
n = 50 с−1 , после выключения тока двигаясь равнозамедленно, остановился, сделав полное число оборотов N =1680 . Найти угловое ускорение якоря.
16
Динамика поступательного движения
Динамика изучает механическое движение тел в связи с действующими на них силами. Сила, действующая на тело, является мерой взаимодействия его с окружающими объектами и приводящая к изменению скорости движущегося тела. В основе механики лежат 3 закона Ньютона.
1 закон Ньютона: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие другого тела не выведет его из этого состояния.
2 закон Ньютона: ускорение, приобретаемое телом под действием внешнего воздействия, прямо пропорционально величине этого воздействия и обратно пропорционально массе тела:
ar = ∑mFi .
3 закон Ньютона: два тела действуют друг на друга с силами, равными по величине и противоположными по направлению:
F12 = −F21 .
Количеством движения или импульсом тела массой m , движущегося со скоростью v , называется величина
p = mv .
Второй закон Ньютона можно представить в общей форме
Fr = dpdt ,
то есть изменение количества движения тела пропорционально действующей силе и происходит в направлении этой силы.
Сила трения скольжения пропорциональна силе нормального давления N , с которой одно тело действует на другое:
Fтр = kN ,
где k – коэффициент трения.
Закон всемирного тяготения: любые два тела (материальные точки) притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:
F = G m1m2 , r2
где G = 6.67 10−11 Н м2 кг−2 – гравитационная постоянная.
17

Задача 2.1. На наклонной плоскости с углом к горизонту α нахо-
 дится тело массой m2 , связанное невесомой нитью с телом массой m1 . Найти ускорение этих тел, если известно, что тело m1 опускается. Тре-
дится тело массой m2 , связанное невесомой нитью с телом массой m1 . Найти ускорение этих тел, если известно, что тело m1 опускается. Тре-  нием в блоке пренебречь. Коэффициент трения
нием в блоке пренебречь. Коэффициент трения
|
тела m2 о наклонную плоскость равен k . |
|
Дано: |
Решение: |
|
m1 |
Изобразим все силы, действующие на каждое тело. |
|
m2 |
Тогда уравнения движения (второй закон Ньютона) каж- |
|
дого тела будут иметь вид: |
||
α |
||
T + N + m2 gr + Fтр = m1ar , |
||
k |
||
|
T + m1gr = m1ar . |
|
a −? |
Здесь учтено, что нить нерастяжима, поэтому ускорения |
|
|
тел по модулю будут равны. Вектор ускорения направим, |
|
|
как показано на рисунке. |
Для описания движения первого тела выберем направление оси системы отсчета вертикально вниз, а для второго тела направление одной из осей возьмем вдоль наклонной плоскости, а другой – перпендикулярно.
Тогда уравнения движения в проекциях на координатные оси будут выглядеть следующим образом:
T − Fтр − m2 g sin α = m2a ,
N − m2 g cos α = 0 ,
−T + m1g = m1a .
Сила трения скольжения равна при этом
Fтр = kN = km2 g cos α .
Тогда можно написать
T −m2 g(k cos α +sin α) = m2 a ,
−T + m1g = m1a .
Складывая два последних уравнения, получим
a = g m1 − m2 (k cos α +sin α) . m1 + m2
18
Задача 2.2. Определить ускорения грузов массами m1 , m2 и m3 в системе блоков, показанной
на рисунке. Массой блока и нитей пренебречь. Трение отсутствует.
Дано: |
Решение: |
|
|
m1 |
Изобразим все силы, дейст- |
||
m2 |
вующие на каждое тело. Ось x |
||
системы отсчета направим вер- |
|||
m3 |
|||
тикально вниз, начало |
отсчета |
||
a1 −? |
возьмем в центре верхнего блока. |
||
a2 −? |
Тогда уравнения движения каж- |
||
дого тела в проекциях на вы- |
|||
a3 −? |
|||
бранную ось будут иметь вид: |
|||
|
m1a1 = m1g −T1 , |
|
|
|
m2 a2 = m2 g −T2 , |
(1) |
|
|
m3a3 = m3 g −T3 . |
|
|
Так как в условиях задачи данные приведены в общем виде, мы не можем сразу определить характер движения каждого тела, какое
тело будет опускаться, а какое подниматься. 
 Поэтому ускорения в левых частях системы (1)
Поэтому ускорения в левых частях системы (1) 








 оставляем в общем случае, потому что оно яв-
оставляем в общем случае, потому что оно яв- 





 ляется не причиной, а следствием движения.
ляется не причиной, а следствием движения. 
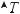
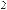
Если при решении задачи ускорение какого- 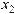








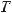 либо тела даст положительную величину, то оно
либо тела даст положительную величину, то оно 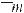
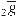
 будет двигаться вниз по оси x , если отрица-
будет двигаться вниз по оси x , если отрица- 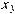











 тельную – то против оси x .
тельную – то против оси x . 
По условию задачи трение отсутствует, 


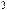 массу блоков и нити не учитываем, нить считаем нерастяжимой. Тогда для сил натяжения нитей можно записать следующие соотношения:
массу блоков и нити не учитываем, нить считаем нерастяжимой. Тогда для сил натяжения нитей можно записать следующие соотношения:
T2 =T3 =T , T1 = 2T .
Тогда систему (1) запишем в виде:
m a |
= m g − 2T |
, |
|
1 1 |
1 |
|
|
m2a2 = m2 g −T , |
(2) |
||
m a |
= m g −T. |
|
|
3 3 |
3 |
|
|
|
|
|
19 |
