
Metod-zaochn
.pdf
Имеем систему трех уравнений с четырьмя неизвестными. Для однозначного его решения необходимо еще одно уравнение. Для его получения поступим следующим образом. Запишем выражение для длины каждой нити с учетом того, что длины нитей постоянны. Из рисунка видно, что
l1 = x1 + πR1 + x0 = const1, |
|
(3) |
|||
l2 = x2 − x0 + πR2 + x3 − x0 = const2 , |
|||||
|
|||||
где R1 и R2 – радиусы блоков. Взяв вторые производные каждого уравне- |
|||||
ния системы (3), с учетом x1 = a1 , |
x2 = a2 , |
x3 = a3 , |
x0 = a0 , где a0 – уско- |
||
&& |
&& |
&& |
&& |
|
|
рение нижнего подвижного блока, получим соотношение, связывающее ускорения грузов:
|
|
|
|
|
|
|
a2 + a3 + 2a1 = 0 . |
|
|
|
|
|
(4) |
|||||||||
Решая совместно (2) и (4), получим ответ: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
= g |
m1 (m2 + m3 ) − 4m2m3 |
|
, |
|
a |
|
= g |
m1(m2 −3m3 ) + 4m2m3 |
|
, |
||||||||||
m (m + m ) + 4m m |
|
m (m + m ) + 4m m |
|
|||||||||||||||||||
|
1 |
|
|
|
2 |
|
|
|||||||||||||||
|
|
1 |
2 |
3 |
|
2 |
3 |
|
|
|
|
|
1 |
2 |
3 |
2 |
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
a |
= g |
m1(m3 |
−3m2 ) + 4m2m3 |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 |
m1 |
(m2 |
+ m3 ) + 4m2m3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 2.3. Тело массой m =1 кг движется так, что пройденное расстояние S от времени дается уравнением S = b sin ωt , где b = 5 см, ω = πрад/с. Найти ускорение, силу и импульс тела через 16 с после начала движения.
Задача 2.4. Тело массой m =1 кг движется так, что его координаты
x и y |
изменяются |
от времени следующим |
образом: x = b −ct + dt2 , |
y = et3 , |
где d =1 м/c2 , |
e = 2 м/c3 . Определить ускорение тела и действую- |
|
|
|
щую на тело силу к концу 5-й секунды. |
|
|
|
Задача 2.5. |
На горизонтальном столе |
|
|
лежат два тела массы M =1 кг каждое, связан- |
|
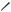
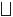
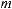 ное невесомой нерастяжимой нитью (см. рису-
ное невесомой нерастяжимой нитью (см. рису-  нок). Тело 2 связано такой же нитью с грузом
нок). Тело 2 связано такой же нитью с грузом
20
m = 0,5 кг. Блок невесомый, трением в блоке можно пренебречь. Коэффициент трения первого тела со столом k1 = 0,1 , второго – k2 = 0,15 . Найти ускорение движения тел.
Задача 2.6. На наклонной плоскости с углом к горизонту α находится тело m2 , свя-
занное невесомой нитью с телом m1 . Коэффициент трения между телом m2 и наклонной
плоскостью равен k . Массой блока и трением в 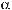 нем можно пренебречь. Вначале оба тела не-
нем можно пренебречь. Вначале оба тела не-
подвижны. Найти отношение масс m1 / m2 , при котором тело m1 начнет: а) опускаться; б) подниматься.
Задача 2.7. Тело массой m расположено на горизонтальной плоскости. Коэффициент трения покоя между телом и плоскостью равен k . С
каким ускорением будет двигаться тело, если к нему приложить силу F под углом α к горизонтали.
Задача 2.8. Система блоков с грузами состоит из двух неподвижных блоков и одного подвижного (см. рисунок). Через блоки перекинута нерастяжимая нить, на концах
которой подвешены грузы с массами m1 и
m3 , а к оси подвижного блока подвешен груз 
 массы m2 . Определить ускорение каждого из
массы m2 . Определить ускорение каждого из 
грузов, если массой блоков и нити, а также трением можно пренебречь.
Задача 2.9. Камень, пущенный по поверхности льда со скоростью v0 = 2 м/с, прошел до остановки расстояние S = 20,4 м. Найти коэффициент
трения k камня о лед.
Задача 2.10. Вдоль наклонной плоскости с углом α начинает скользить тело со скоростью v0 . Поднявшись на максимальную высоту,
оно возвращается к начальному положению. Коэффициент трения тела о плоскость k . Определить скорость тела после возвращения в исходное состояние, а также интервал времени ∆t между началом движения и концом.
21
Законы сохранения импульса и энергии
Из общей формы второго закона Ньютона следует, что если геометри-
ческая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, то есть не меняется со временем. В частно-
сти, это имеет место, когда система замкнута. Это положение называется
законом сохранения импульса:
p = p1 + p2 +K+ pn = const .
Работа силы F на перемещении ds есть скалярное произведение dA = (F dS) = F dS cosα .
Кинетическая энергия материальной точки массы m , движущейся со скоростью v , равна
= mv2
Wкин 2 .
Потенциальная энергия тела или системы тел – это энергия, обусловленная взаимодействием тел друг с другом. Потенциальная энергия системы определена не однозначно, а с точностью до произвольной постоянной.
Потенциальная энергия тела массы m в однородном поле тяжести, поднятого на высоту h над нулевым уровнем, равна произведенной при подъеме работе:
Wp = mgh .
Потенциальная энергия растянутой (или сжатой) пружины равна работе при ее деформации:
Wp = 12 kx2 ,
где x – растяжение пружины, k – жесткость пружины.
Полная механическая энергия тела или системы тел равна
W =Wкин +Wp .
Закон сохранения энергии:
W = const ,
то есть, если в системе действуют только консервативные силы (сила тяжести, сила упругости) и нет действия неконсервативных сил (сил трения), то полная механическая энергия системы остается постоянной. Другими словами, могут происходить лишь превращения потенциальной энергии в кинетическую и обратно.
22
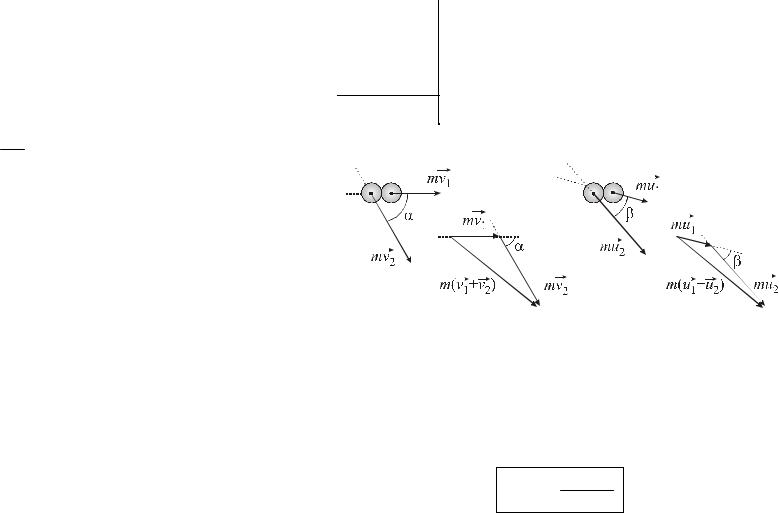
Задача 3.1. Два одинаковых шарика налетают друг на друга со скоростями v1 и v2 под углом α и разлетаются после абсолютно упругого уда-
ра со скоростями
Дано: v1
v2
α
u1 u2
β−?
u1 и u2 . Найти угол β разлета частиц после соударения.
Решение:
По закону сохранения импульса суммарный импульс двух частиц до взаимодействия p = p1 + p2 равен
суммарному импульсу после взаимодействия p′ = p1′ + p2′
(см. рисунок):
p1 + p2 = p1′ + p′2 .
По условию задачи частицы одинаковые, то есть m1 = m2 = m . Тогда можно записать:
v1 + v2 = u1 +u2 .
Используя теорему косинусов, получим:
v2 |
+ v2 |
− 2v v |
2 |
cos(π−α) = u2 |
+u2 |
− 2u u |
2 |
cos(π−β) . |
(1) |
1 |
2 |
1 |
1 |
2 |
1 |
|
|
Запишем закон сохранения энергии:
mv2 |
+ |
mv2 |
= |
mu2 |
+ |
mu2 |
(2) |
1 |
2 |
1 |
2 . |
||||
2 |
|
2 |
|
2 |
|
2 |
|
Тогда выражение (1) с учетом (2) запишем в виде: v1v2 cos α = u1u2 cos β,
или, окончательно, получим ответ:
β= arccos v1v2 cos α .
u1u2
23

Задача 3.2. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки повеса стержня l =1м. Найти скорость пули, если известно, что стержень отклонился после удара пули на угол α =10°.
Дано: |
Решение: |
|
|
l =1м |
Как видно из рисунка, угол отклонения стержня α |
||
α =10° |
связан с высотой h , на которую поднимется шар: |
|
|
M =1000 |
h = l (1 −cos α) . |
поднятого на высоту |
|
m |
Потенциальная энергия шара, |
||
v −? |
h над его первоначальном положении (Wp = 0 ): |
|
|
|
Wp = (M + m)gh . |
|
|
|
Теперь |
возникает |
вопрос: |
|
равна ли эта энергия в конечном |
||
|
состоянии ее начальной энергии, |
||
|
то есть кинетической |
энергии |
|
|
пули mv2 / 2 ? Оказывается что |
||
нет, потому что при неупругом
ударе часть механической энергии переходит во внутреннюю.
Рассмотрим еще одно, промежуточное состояние системы – сразу после окончания удара, когда пуля уже застряла в шаре, но стержень еще вертикален. Энергия системы в этом состоянии представляет собой просто кинетическую энергию шара с пулей:
Wкин = (M + m) u2 , 2
где u – их общая скорость.
После того как неупругий удар уже закончился, энергия больше теряться не будет, и можно записать закон сохранения энергии:
Wкин =Wp , или
(M + m) u2 = (M + m)gh . 2
Значение скорости u определим из закона сохранения импульса: mv = (M + m) u .
24
Из последних двух уравнений, с учетом выражения для h , имеем:
|
|
M |
|
α |
|
v = 2 1 |
+ |
m |
gl sin |
2 |
. |
Или, с учетом условий задачи, получим:
v = 550 м/c .
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 3.3. На горизонтальной поверхности лежит куб, сторона которого равна l , а масса m . Каким образом нужно перемещать куб – кантовать его или двигать по поверхности, чтобы на пути S = nl ( n – целое число) совершить наименьшую работу? Коэффициент трения между поверхностью куба и горизонтальной поверхностью k = 0.3 .
Задача 3.4. На носу и корме лодки массой M и длиной l , стоящей неподвижно в озере, находятся два рыболова массами m1 и m2 . Найти смещение лодки ∆l , когда рыболовы поменяются местами.
Задача 3.5. Молекула массой 4,65 10−26 кг, летящая со скоростью 600 м/с, ударяется о стенку сосуда под углом 60° к нормали и под таким же углом упруго отскакивает от нее без потери скорости. Найти импульс силы, полученной стенкой за время удара.
Задача 3.6. Платформа с песком массой M движется горизонтально со скоростью v . Камень массой m попадает в песок и движется вместе с тележкой. Определить скорость u тележки после попадания в песок камня, летящего со скоростью w в двух случаях: а) по вертикали; б) по горизонтали навстречу тележке. Трение не учитывать.
Задача 3.7. Какая часть кинетической энергии перейдет в теплоту при неупругом столкновении двух одинаковых тел, движущихся до удара с равными по модулю скоростями под прямым углом друг к другу?
Задача 3.8. Тело брошено вертикально вверх со скоростью 16 м/с. На какой высоте h его кинетическая энергия равна потенциальной? Сопротивление воздуха не учитывать.
25

Задача 3.9. Маленькое тело кладут на наклонную плоскость, составляющую угол α с горизонтом, и отпускают. В нижней точке плоскости тело ударяется об упор, отскакивает без потери скорости и поднимается обратно по наклонной плоскости на некото- 

 рую высоту. Найдите эту высоту h2 , если
рую высоту. Найдите эту высоту h2 , если
начальная высота тела h1 , а коэффициент трения тела о плоскость k ( k < tg α).
Задача 3.10. В детском пистолете шарик кладут на пружину, укрепленную внутри ствола. Пружину сжимают на длину ∆l = 5 см, а потом отпускают, направив ствол вертикально вверх. Шарик взлетает на высоту H = 0,5 м. Какое максимальное ускорение приобрел шарик? Шарик отры-
вается от пружины в тот момент, когда она полностью распрямится. Трением, сопротивлением воздуха и массой пружины пренебречь.
Задача 3.11. Тело массой m съезжает с высоты h гладкой на-
клонной плоскости и начинает
скользить по тележке массой
M , находящейся на гладкой
горизонтальной плоскости. Ко-
эффициент трения тела о по-
верхность тележки k . На какое
расстояние переместится тело относительно тележки?
Задача 3.12. Нить длины l с шариком массы m на конце отклонили от вертикали на 90° и отпустили. На каком наименьшем расстоянии под точкой подвеса нужно поставить гвоздь, чтобы нить, налетев на него, порвалась? Нить выдерживает силу натяжения T .
Задача 3.13. На краю стола высоты h лежит маленький шарик массы M . В него попадает пуля массы m , летящая горизонтально со скоростью v , направленной в центр шарика. Пуля застревает в шарике. На каком расстоянии от стола по горизонтали шарик упадет на Землю?
26
Динамика вращательного движения твердого тела
Абсолютно твердое тело – это такая идеализированная система, в которой расстояния между любыми точками остаются неизменными при любых движениях системы.
Движение твердого тела в общем случае можно разложить на поступательное и вращательное. Поступательное это такое движение, при котором любая линия, проведенная в теле, при движении остается параллельной самой себе. При поступательном движении динамика твердого тела сводится к динамике одной точки, в качестве которой берут центр масс. Центром масс системы называется точка C , положение которой задается ра-
диус-вектором rC , определяемым следующим образом:
|
|
|
|
|
|
|
N |
r |
|
rr |
|
r |
|
r |
r |
|
∑miri |
||
= m1r1 |
+ m2r2 |
+K+ mN rN = i =1 . |
|||||||
C |
|
m1 |
+ m2 |
+K+ mN |
|
|
m |
|
|
|
|
|
|
||||||
Вращательное это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Моментом силы F относительно точки O называется векторное произведение радиус-вектора силы относительно точки O на вектор силы
M =[rr, F] .
Моментом M нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки:
M = ∑Mi = ∑[rri , Fi ] .
Моментом импульса p материальной точки относительно точки O
называется векторное произведение
L =[rr, pr] .
Для системы материальных точек моментом импульса относительно некоторого начала O называется сумма моментов этих точек относительно того же начала.
Момент силы и момент импульса относительно точки есть вектор. Момент силы и момент импульса относительно оси есть проекция на эту ось момента относительно точки, лежащей на той же оси, то есть является скалярной величиной.
27
Уравнение моментов (или закон изменения момента импульса): dLdt = Mr ,
то есть производная по времени от момента импульса материальной точки (системы материальных точек) относительно произвольного неподвижного начала равна геометрической сумме моментов всех внешних сил относительно того же начала O .
Если момент внешних сил относительно неподвижного начала O равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени. Это утверждение называется законом сохранения момента импульса. В частности, это имеет место для изолированной системы материальных точек. Если имеет место случай центральных сил, когда направления всех сил, действующих на материальные точки системы, проходят через неподвижный центр O , то момент импульса системы относительно точки O также остается постоянным во времени.
Моментом инерции системы материальных точек относительно некоторой оси называется величина, равная сумме произведений масс материальных точек на квадраты расстояний их до оси вращения:
N
I = ∑miri2 .
i =1
Основное уравнение динамики вращательного движения:
I ddtω = Mr ,
то есть произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.
Момент импульса материальной точки при вращательном движении можно определить также как произведение момента инерции точки на угловую скорость:
r
L = I ω.
Если вещество в теле распределено непрерывно, то его момент инерции определяется в виде интеграла
I = ∫r2dm ,
где r – расстояние от элемента массы dm до оси вращения.
Момент инерции тела характеризует меру инертности при вращательном движении.
28
Частные случаи момента инерции:
– момент инерции бесконечно тонкого круглого кольца (окружности) радиуса R относительно оси, проходящей через центр симметрии и перпендикулярной плоскости кольца:
I= mR2 ;
–момент инерции полого однородного цилиндра радиуса R с бесконечно тонкими стенками относительно его геометрической оси:
I= mR2 ;
–момент инерции однородного сплошного диска радиуса R относительно оси, проходящей через центр диска и перпендикулярной к его плоскости:
I= 12 mR2 ;
–момент инерции однородного сплошного цилиндра радиуса R относительно его продольной геометрической оси:
I= 12 mR2 ;
–момент инерции тонкого однородного стержня длины l относительно перпендикулярной оси, проходящей через центр масс:
I= 121 m l2 ;
–момент инерции сплошного однородного шара радиуса R :
I = 52 mR2 .
Теорема Гюйгенса–Штейнера:
I = IC + ma2 ,
то есть момент инерции тела относительно любой оси равен моменту инерции этого тела относительно оси, проходящей через центр масс параллельно заданной, сложенному с произведением массы тела на квадрат расстояния между осями.
Если материальная точка вращается по окружности, то элементарная работа при повороте на угол dϕ равна
dA = M dϕ .
Кинетическая энергия вращающегося твердого тела определяется как
Wкин = I ω2 2 .
29
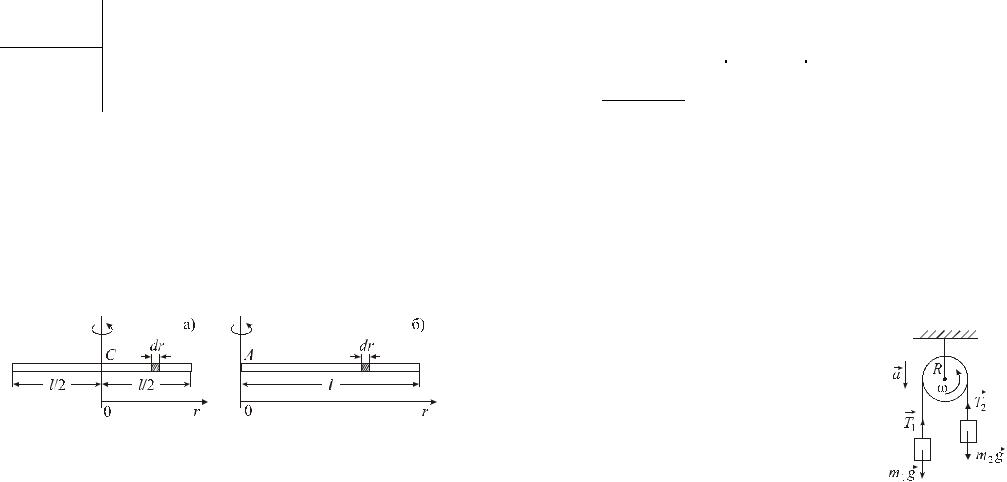
Задача 4.1. Найти момент инерции тонкого однородного стержня длины l и массы m : а) относительно перпендикулярной к стержню оси, проходящей через центр масс; б) относительно перпендикулярной к стержню оси, проходящей через конец стержня.
Дано: |
Решение: |
l |
Предполагается, что стержень однородный, то есть |
mвещество распределено в нем с постоянной плотностью, и бесконечно тонкий, то есть поперечные размеры стержня
IC −? |
очень малы по сравнению с его длиной. |
|
Рассмотрим сначала случай, когда ось проходит че- |
||
I A −? |
||
рез центр стержня C , который является центром масс. |
||
|
Выделим бесконечно малый элемент стержня массой dm , |
находящийся на расстоянии r от оси вращения и имеющий длину dr (см. рис.). Объем такого элемента равен dV = dm / ρ = S dr , где ρ – плотность стержня, S – площадь его поперечного сечения. С учетом ρ = m / V , где V = S l – объем всего стержня, получим
|
|
dm = m dr . |
|
|
|
|
|
|
|||
|
|
|
|
l |
|
|
|
|
|
|
dIC = r2dm , а мо- |
Момент инерции этого элемента найдется по формуле |
|||||||||||
мент инерции всего стержня определяется интегралом |
|
|
|||||||||
|
2 |
|
m l / 2 2 |
|
1 |
|
2 |
|
|
||
IC = ∫r |
|
dm = |
l |
∫r |
dr = |
|
|
m l |
|
. |
(1) |
|
12 |
|
|||||||||
|
|
|
−l / 2 |
|
|
|
|
|
|||
Пусть теперь ось проходит через конец стержня A . Тогда при определении момента инерции стержня пределы интегрирования будут иными:
I A = ∫r |
2 |
dm = |
m l |
2 |
dr = |
1 |
m l |
2 |
. |
(2) |
|
|
l |
∫r |
|
3 |
|
||||||
|
|
|
0 |
|
|
|
|
|
|
||
30
Этот результат можно получить также с использованием теоремы Гюйген- са–Штейнера. Действительно,
l |
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
||
I A = IC + m |
|
|
= |
|
|
m l |
|
+ |
|
m l |
|
= |
|
m l |
|
. |
2 |
12 |
|
4 |
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следует заметить, что формулы (1) и (2) не применимы к стержню конечной толщины.
Ответ: |
IC = |
|
|
1 |
|
m l2 |
, |
I A = |
1 m l2 |
. |
|
12 |
|||||||||||
|
|
|
|
|
3 |
|
|||||
Задача 4.2. |
|
Определить угловое ускорение блока радиусом R с |
|||||||||
моментом инерции I , через который перекинута нить с грузами массой m1 и m1 . Трением пренебречь.
Дано: |
Решение: |
|
R |
Ранее мы рассматривали движение тел, перекинутых |
|
I |
через блоки (задача 2.2.), пренебрегая массой блоков. |
|
m1 |
Теперь, в данной задаче, приведен момент инерции бло- |
|
m2 |
ка, это означает, что он обладает массой. Тогда помимо |
|
уравнений движений для грузов m1 и m 2 необходимо |
||
|
||
β−? |
записать уравнение движения блока. Таким уравнением |
|
|
будет уравнение динамики вращательного движения, так |
как блок будет вращаться под действием сил T1 и T2 вокруг своей оси,
проходящей через центр масс.
Пусть m1 > m2 , тогда груз m1 будет опускать-
ся, а блок вращаться против часовой стрелки (см. рис.). В результате получим следующую систему уравнений:
m1a = m1g −T1,m2a =T2 − m2 g,I β = (T1 −T2 )R.
Здесь учтено, что нить нерастяжима, поэтому грузы m1 и m2 будут двигаться с одинаковым по мо-
дулю ускорением.
31

Учитывая связь между линейным и угловым ускорениями a = βR , запишем систему в виде:
m1βR = m1g −T1,m2 βR =T2 − m2 g,I β = (T1 −T2 )R.
Исключая неизвестные T1 и T2 , получим ответ:
β = |
|
g(m1 − m2 ) |
. |
|
(m + m + I / R2 ) R |
|
|||
|
1 |
2 |
|
|
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 4.3. К ободу однородного диска радиусом R = 0,2 м приложена касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения M = 4,9 Н м . Найти массу диска m , если известно, что диск
вращается с угловым ускорением β =100 рад/c2 .
Задача 4.4. Однородный стержень длиной l =1м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением β вра-
щается стержень, если на него действует момент сил M = 98,1 10−3 Н м .
Задача 4.5. Маховик, момент инерции которого I = 63,6 кг м2 , вращается с угловой скоростью ω = 31,4 рад/c . Найти момент сил тормо-
жения M , под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
Задача 4.6. На барабан массой m = 9 кг намотан шнур, к концу которого привязан груз массой m1 = 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.
Задача 4.7. Две гири с массами m1 = 2 кг и m2 =1 кг соединены нитью, перекинутой через блок массой m =1 кг. Найти ускорение a , с ко-
32
торым движутся гири, и силы натяжения T1 и T2 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Задача 4.8. Найти линейные ускорения центров масс шара, диска и обруча, скатывающихся без скольжения с наклонной плоскости. Угол плоскости α = 30 °, начальная скорость всех тел v0 = 0 .
Задача 4.9. Мальчик катит обруч по горизонтальной поверхности со скоростью v = 7,2 км/ч. На какое расстояние может вкатиться обруч на
горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути.
Задача 4.10. Карандаш длиной l =15 см, поставленный вертикально, начинает падать на стол. Какую угловую скорость ω и линейную скорость v будут иметь в конце падения середина и верхний конец карандаша?
Задача 4.11. Однородный стержень длиной l =1м подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол α надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость v = 5 м/с?
Задача 4.12. Колесо радиусом R и массой m стоит перед ступенькой высотой h . Какую наименьшую горизонтальную силу F нужно приложить к оси колеса, чтобы оно могло подняться на ступеньку? Трением пренебречь.
Задача 4.13. Лестница длиной l и массой m приставлена к стене под углом α к горизонтали. Коэффициент трения между лестницей и полом k1 , а между лестницей и стеной k2 . Найти наименьший угол α , при
котором лестница еще находится в равновесии, а также реакции пола и стены.
Задача 4.14. К гладкой вертикальной стене подвесили на тросе однородный шар массой m . Трос образует со стеной угол α . Определить силу T натяжения троса и силу давления F шара на стену.
33

Кинематика и динамика гармонических колебаний
Колебаниями называется такое движение, при котором система при своем движении многократно проходит через определенное положение, например, положение равновесия. Если повторения происходят через одинаковое время, то колебания являются периодическими, а интервал времени, в течение которого происходит повторение, называется периодом.
Свободными или собственными колебаниями называются такие коле-
бания, которые совершает система, выведенная из положения равновесия, и предоставленная самой себе.
Простейший вид колебаний – гармонические, то есть такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса:
x = Acos(ω0t + ϕ0 ) ,
где A – амплитуда (наибольшее отклонение системы от положения равновесия), ϕ = ω0t + ϕ0 – фаза колебаний (показывает состояние колеблющей-
ся системы в данный момент времени), ϕ0 – начальная фаза колебаний, ω0 – круговая или циклическая частота собственных колебаний.
Скорость и ускорение точки, совершающей колебания, определяются соотношением:
v = x& = −Aω0 sin(ω0t + ϕ0 ) = Aω0 cos(ω0t + ϕ0 + π/ 2) , a = &x&= −Aω02 cos(ω0t + ϕ0 ) = Aω02 cos(ω0t + ϕ0 + π) .
Потенциальная и кинетическая энергии колеблющейся точки:
|
|
Wp = |
kx2 |
= |
kA2 |
cos2 (ω0t + ϕ0 ) , |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
||||
W = |
mv2 |
= |
mA2ω02 |
sin 2 (ω t + ϕ |
) = |
kA2 |
sin 2 |
(ω |
t + ϕ |
) . |
||||
|
|
|
||||||||||||
k |
2 |
2 |
|
|
0 |
0 |
2 |
|
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Кинетическая и потенциальная энергии в отдельности не остаются постоянными, а совершают гармонические колебания вокруг общего сред-
него значения kA2 / 4 с удвоенной круговой частотой 2ω0 .
Полная энергия точки, колеблющейся без затухания, остается величиной постоянной:
W =Wp +Wk = kA22 .
34
Период пружинного маятника (тело массой m , прикрепленное к пружине жесткостью k ) равен:
T = 2π = 2π m . ω0  k
k
Период математического маятника (идеализированная система, со-
стоящая из невесомой и нерастяжимой нити длиной l , на которую подвешена масса, сосредоточенная в одной точке) равен:
T = 2π gl ,
gl ,
где g – ускорение свободного падения.
Период физического маятника (твердое тело произвольной формы, которое может колебаться вокруг точки подвеса, находящейся выше центра масс) равен:
T = 2π rmgI ,
rmgI ,
где I – момент инерции маятника относительно его оси вращения, m – масса маятника, r – расстояние от оси вращения до центра масс.
Задача 5.1. Материальная точка массой 10 г колеблется по закону x = 0,05 cos(0,6t +0,8) (м). Найти максимальную силу, действующую на
точку, и полную энергию колеблющейся точки.
Дано: |
Решение: |
|
m =10 г |
Сравнивая уравнение, данное в задаче |
|
x = 0,05 cos(0,6t +0,8) |
x = 0,05 cos(0,6t +0,8) , |
|
|
с уравнением гармонических колебаний в общем |
|
Fmax −? |
||
виде |
||
Wmax −? |
||
x = Acos(ω0t + ϕ0 ) , |
находим:
A = 5 10−2 м, ω0 = 0,6 рад/с, ϕ0 = 0,8 рад.
Модуль силы, вызывающей гармонические колебания, равен
F = m | ar |= mAω02 cos(ω0t + ϕ0 ) ,
откуда получаем
35
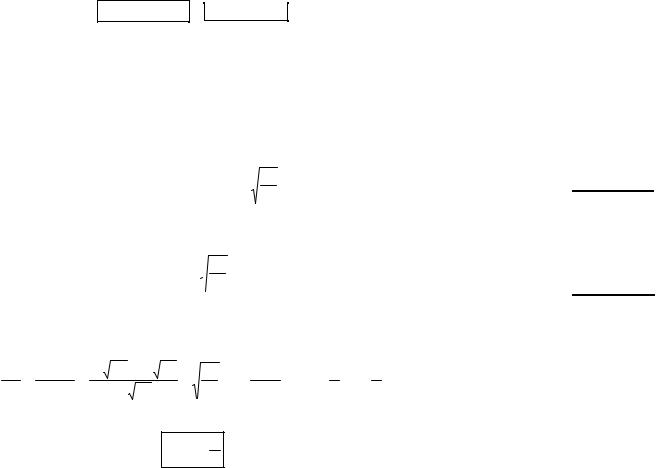
Fmax = mAω02 ; Fmax =1,8 10 −4 Н=180 мкН.
Полная энергия колеблющейся точки
W = 12 mA2ω02 ; W = 4,5 10 −6 Дж= 4,5 мкДж.
Ответ:
Fmax =180 мкН , W = 4,5 мкДж .
Задача 5.2. Период колебаний математического маятника на уровне Земли равен T0 . Насколько изменится период колебаний маятника, если
его поднять на высоту H над поверхностью Земли? Землю считать шаром радиуса R .
Дано: |
Решение: |
|
T0 |
Период колебаний математического маятника на |
|
H |
поверхности Земли будет равен: |
|
R |
T = 2π l , |
|
|
0 |
g0 |
|
|
|
∆T −? |
где g0 = GM / R2 ( M – масса Земли, R – радиус Земли), |
|
|
а на высоте h над поверхностью Земли период будет |
|
l Th = 2π  gh ,
gh ,
где gh = GM /(R + h)2 .
Относительное изменение периода колебаний маятника составит величину:
∆T |
= |
T |
−T |
= |
1/ |
gh −1/ g0 |
= |
g |
0 |
−1 = |
R + h |
−1 =1 + |
h |
−1 |
= |
h |
, |
T0 |
h |
0 |
|
1/ g0 |
|
|
|
|
|||||||||
|
|
T0 |
|
|
|
gh |
|
R |
|
R |
|
|
R |
|
|||
откуда получаем ответ:
∆T = T0 Rh .
36
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 5.3. Колебания материальной точки совершаются по закону x = 0,03 cos π(t +0,5) . Амплитуда и период колебаний заданы в системе СИ.
Определить наибольшие значения скорости и ускорения. Чему равна фаза колебаний спустя 5 с от начала движения?
Задача 5.4. Смещение гармонического осциллятора в зависимости от времени дается выражением x = 2,4 cos(2πt / 4 +π/ 6) , где x измерена в
метрах, а t – в секундах. Найти: а) период и частоту колебаний; б) смещение и скорость в момент времени t = 0 ; в) скорость и ускорение в момент времени t =10 с.
Задача 5.5. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = −6 sin 2πt . Записать зависи-
мость смещения этой точки от времени.
Задача 5.6. Частица движется с постоянной скоростью 24 м/с по окружности с центром в начале координат. В момент времени t = 0 частица находится в точке x = 3,0 м; y = 4,2 м. Чему равна частота вращения?
Чему равна начальная фаза ϕ0 ? Каким выражением описывается траектория этой частицы в плоскости x , y ?
Задача 5.7. Амплитуда гармонических колебаний материальной точки A = 2 см, полная энергия колебания W = 0,3 мкДж. При каком сме-
щении x от положения равновесия на колеблющуюся точку действует сила
F = 22,5 мкН?
Задача 5.8. Как изменится период вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от последовательного соединения пружин перейти к параллельному их соединению?
Задача 5.9. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний возрастает в 2 раза. Определить массу первоначально подвешенного груза.
37

Задача 5.10. Груз массой m осторожно прикрепляют к концу свободно висящей пружины. Когда груз освобождают, он опускается на 30 см, а затем начинает колебаться. Чему равна частота колебаний?
Задача 5.11. Однородный круглый диск радиусом R подвешен за край. Чему равна частота его малых колебаний относительно точки подвеса?
Задача 5.12. Найти амплитуду A и начальную фазу ϕ0 гармони-
ческого колебания, полученного от сложения одинаково направленных колебаний, заданных следующими уравнениями x1 = 0,02 cos(5πt +π/ 2) м и
x2 = 0,03 cos(5πt +π/ 4) м.
Задача 5.13. Точка подвеса математического маятника, период собственных колебаний которого равен T0 =1с, совершает синусоидальные
колебания с амплитудой Aп =1см и периодом T =1,1 с. Какова амплитуда A установившихся колебаний маятника?
Волны. Звуковые волны
Волнами называются возмущения, распространяющиеся в среде (или в вакууме) и несущие с собой энергию.
Различают волны продольные и поперечные. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной – в направлениях, перпендикулярных к направлению распространения волны.
Расстояние λ, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Связь
длины волны с периодом колебаний
λ = vT ,
где v – скорость распространения волны, которая является фазовой скоростью.
Уравнение плоской незатухающей волны
ξ = Acos(ωt − kx + ϕ0 ) ,
38
где A – амплитуда колеблющихся точек, ω = 2π/ T – циклическая частота,
k – волновое число, равное
k = 2λπ = ωv .
Для волны, распространяющейся в произвольном направлении, уравнение будет иметь вид
ξ(rr, t) = Acos(ωt − krr + ϕ0 ) ,
где k – волновой вектор, равный по модулю волновому числу и имеющий направление нормали к волновой поверхности.
Фазовая скорость продольных волн равна
v = |
E |
, |
|
ρ |
|
где E – модуль Юнга, ρ – плотность среды. |
||
Фазовая скорость поперечных волн |
|
|
v = |
G |
, |
|
ρ |
|
где G – модуль сдвига.
Средняя плотность энергии, то есть энергия волны, приходящая на единицу объема и усредненная по периоду, определяется выражением
< w >= 12 ρω2 A2 .
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность
Ф = dWdt .
Плотность потока энергии численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия,
rj = w vr .
Плотность потока энергии является векторной величиной с направлением, совпадающим с направлением распространения волны и переноса энергии.
Среднее по времени значение плотности потока энергии, переносимой волной, называется интенсивностью волны.
39
