
MathCad_Labs
.pdfЛабораторная работа 10. Метод наименьших квадратов. Построение конкретных нелинейных моделей
10.1Нелинейная регрессия
В лабораторной работе №8 мы имели дело с частным случаем регрессии - линейной регрессией. Теперь рассмотрим общий случай и общую постановку задачи регрессионного анализа.
Пусть имеется выборка (X, Y) = ((X1, Y1), (X2, Y2), . . . , (Xn, Yn)) из распределения случайной величины ψ = (ξ, η). И пусть известно, что случайные величины ξ и η зависимы. Важное прикладное значение имеет задача о представлении одной из этих величин как функции от другой.
Проведение регрессионного анализа можно разделить на три этапа: выбор формы зависимости (типа уравнения), вычисление параметров выбранного уравнения, оценка достоверности полученного уравнения.
Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, наблюдений расположения точек (Xi, Yi) на плоскости и т.д.
Обозначим через f(x, θ), функцию задающую зависимость среднего значения η от значений ξ (здесь θ = (θ1, . . . , θk) - вектор параметров):
M(η/ξ = x) = f(x, θ).
Уравнение y = f(x, θ) называется уравнением регрессии.
Для определения неизвестных параметров θ1, . . . , θk можно использовать метод наименьших квадратов.
Суть этого метода состоит в том, что наилучшим считается такое положение линии регрессии, при котором сумма квадратов отклонений значений f(Xi, θ) от соответствующих Yi минимальна. Метод состоит в
71
минимизации функции
n
X
Q(θ) = (yi − f(xi, θ))2.
i=1
Приведем пример построения нелинейной регрессии с использованием метода наименьших квадратов.
Пусть при проведении эксперимента получены следующие значения величин x и y:
x |
6 |
6.1 |
6.3 |
6.5 |
6.7 |
7 |
7.5 |
8 |
8.2 |
8.5 |
y |
4.5 |
4 |
3.5 |
3 |
2.5 |
2 |
1.5 |
1 |
0.7 |
0.5 |
Считая справедливой зависимость y(x, D) = D0eD1x, находим неизвестные параметры D0 и D1 c помощью метода наименьших квадратов. В результате получаем следующее уравнение регрессии:
y = 500.1e−0.79x.
Текст программы, реализующей построение уравнения регрессии приведен на рис. 10.1. В данной программе для минимизации функции Q(D) используется встроенная функция Minerr(). Однако минимизацию можно провести известным методом исследования функции нескольких переменных на экстремум с помощью дифференциального исчисления.
72
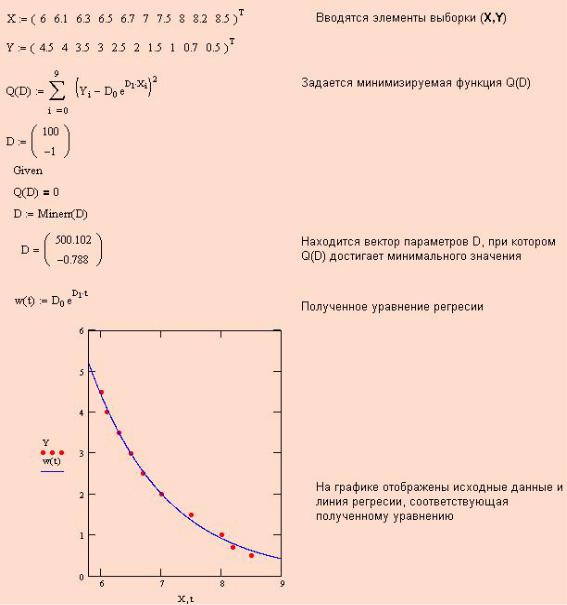
Рис. 10.1. Построение уравнения регрессии с помощью метода наименьших квадратов
10.2Задание к лабораторной работе
В файле regrV.txt (V - это номер вашего варианта) в виде матрицы задана выборка (X, Y). Первый столбец матрицы - значения X, второй столбец - соответствующие значения Y.
1. С помощью метода наименьших квадратов построить уравнения регрессии, считая справедливыми следующие формы зависимости y от x:
а) y = a sin (bx), |
б) y = loga bx, |
в) y = a0 + a1x + a2x2. |
73
Поиск минимума функции Q(D) проводить, исследуя эту функцию на экстремум с помощью частных производных.
2. На одном графике изобразить исходные данные и полученные линии регрессии. Сделать вывод о том, какая из функций наилучшим образом представляет зависимость y от x.
74

Приложение А
Некоторые параметрические семейства распределений
1. Равномерное распределение Ua,b. Функция плотности распределе-
ния и моменты распределения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
, t [a, b], |
|
|
MX = |
b − a |
, |
DX = |
(b − a)2 |
. |
||||||||||||||||||||||||
|
ua,b(t) = |
b |
|
a |
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0,−t |
|
|
[a, b] |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
12 |
|
||||||||||
2. |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Показательное распределение E . Функция плотности распределе- |
|||||||||||||||||||||||||||||||||||||
ния и моменты распределения: |
|
|
|
MX = λ, DX = λ2. |
||||||||||||||||||||||||||||||||||
|
|
eλ(t) = (0, t 0, |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
λe−λt, t > 0, |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Гамма-распределение α,β. Функция плотности распределения: |
||||||||||||||||||||||||||||||||||||||
|
γα,β(x) = βα+1 (α + 1) xαe−β , x > 0 , α > |
|
|
1, β > 0. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
x |
≤ |
0 |
|
|
|
|
|
− |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Моменты |
распределения: MX = (α + 1)β, DX = β2(α + 1). |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Распределение Пуассона Πλ (λ > 0): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
λme−λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P (X = m) = |
|
(m = 0, 1, 2, ...) MX = λ, DX = λ. |
|||||||||||||||||||||||||||||||||||
|
m! |
|||||||||||||||||||||||||||||||||||||
5. Геометрическое распределение Gp: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
P (X = k) = (1 − p)kp, |
p (0, 1), k = 0, 1, 2, ... |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
MX = |
1 − p |
, DX = |
|
|
1 − p |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|||
6. Биномиальное распределение Bpn: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
P |
( |
X |
= |
k |
) = |
Cnpk |
(1 |
− |
p |
n−k |
|
(0 ≤ |
k |
≤ |
n |
, |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
k |
) |
|
|
|
|
|
) |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
MX = np, |
DX = np(1 − p). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
7. Нормальное распределение Na,σ2 . Функция плотности распределения и моменты распределения:
|
1 |
|
(x−a)2 |
||
f(x) = |
σ√ |
|
e− |
2σ2 |
, MX = a, DX = σ2 |
2π |
|||||
75
8. Бета-распределение βm,n. Функция плотности распределения:
βm,n(x) = |
(m) |
|
(n)xm−1 |
(1 − x)n−1 |
, |
x (0, 1) |
||
|
|
(m + n) |
|
|
|
|
||
|
|
· |
0, |
|
|
x |
(0, 1), |
|
где m > 0, n > 0. |
|
|
|
|
|
|
6 |
|
|
|
|
|
m |
|
|
mn |
|
Моменты распределения: MX = m + n, DX = (m + n)2(m + n + 1). 9. Логарифмически нормальное (логнормальное) распределение.
Функция плотности распределения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
e− |
(ln x−a)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
l(x) = |
xσ√ |
|
|
|
|
|
2σ2 |
|
, x > 0, |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
x |
≤ |
0. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
+a |
|
|
|
|
|
|
σ2 |
+2a σ2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MX |
= |
|
e |
|
|
|
, DX |
= |
e |
|
|
|
|
( |
e |
|
|
. |
||||||||||||
Моменты распределения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1) |
|||||||||||||||||||||
10. Распределение χn2 . Функция плотности распределения: |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
n |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
hn(x) = |
2 |
|
n |
|
x |
|
− e− при |
x > 0, , |
|
n = 1, 2, . . . |
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
при |
x ≤ 0. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Моменты распределения: MX = n, DX = 2n. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. Распределение Стьюдента Tk. Функция плотности распределения: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
((k + 1)/2) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
tk(x) = |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, k = 1, 2, . . . |
|||||||||||||||||||||||||||
|
|
|
(k/2) |
|
|
|
(1 + x2/k)(k+1)/2 |
|||||||||||||||||||||||||||||||||||||
πk |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3/2) (k/2 − 1) |
|
|
|
|
|
||||||||||||||||
|
MX = 0; DX = k |
|
|
|
|
|
|
√ |
|
(k/2) |
|
|
|
|
, k > 2. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
||||||||||||||||||||||||||||||||
12. Распределение Фишера Fk,m. Функция плотности распределения: |
||||||||||||||||||||||||||||||||||||||||||||
|
k |
k/2 |
|
((k + m)/2) |
|
|
|
|
|
|
|
|
xk/2−1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
fk,m(x) = |
|
! |
|
|
|
|
|
|
|
, |
|
|
x > 0; k, m > 0. |
|||||||||||||||||||||||||||||||
m |
|
|
(k/2) (m/2) |
(1 + kx/m)(k+m)/2 |
|
|
||||||||||||||||||||||||||||||||||||||
MX = |
|
m |
|
|
|
|
, m > 2; DX = |
|
|
2m2(k + m − 2) |
, m > 4. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k(m − 2)2(m − 4)2 |
||||||||||||||||||||||||||||||||||||
|
|
|
m − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
13. Распределение Коши Km,n. Функция плотности распределения:
1m
km,n(x) = π m + (x − n)2, m > 0, −∞ < n < ∞. MX и DX не существуют.
76
Приложение Б
Tаблица 1
ε |
τε |
ε |
τε |
0.010 |
2.3263 |
0.250 |
0.6745 |
0.025 |
1.9600 |
0.300 |
0.5244 |
0.050 |
1.6449 |
0.350 |
0.3853 |
0.100 |
1.2816 |
0.400 |
0.2533 |
0.150 |
1.0364 |
0.450 |
0.1257 |
0.200 |
0.8416 |
0.500 |
0.0000 |
Квантили стандартного нормального распределения τε
Tаблица 2
k |
p = 0.750 |
p = 0.900 |
p = 0.990 |
p = 0.999 |
|
|
|
|
|
1 |
1.000 |
3.078 |
31.821 |
318 |
2 |
0.816 |
1.886 |
6.965 |
22.3 |
3 |
0.765 |
1.638 |
4.541 |
102 |
4 |
0.741 |
1.533 |
3.747 |
7.173 |
5 |
0.727 |
1.476 |
3.365 |
5.893 |
6 |
0.718 |
1.440 |
3.143 |
5.208 |
7 |
0.711 |
1.415 |
2.998 |
4.785 |
8 |
0.706 |
1.397 |
2.896 |
4.501 |
9 |
0.703 |
1.383 |
2.821 |
4.297 |
10 |
0.700 |
1.372 |
2.764 |
4.144 |
11 |
0.697 |
1.363 |
2.718 |
4.025 |
12 |
0.695 |
1.356 |
2.681 |
3.930 |
13 |
0.694 |
1.350 |
2.650 |
3.852 |
14 |
0.692 |
1.345 |
2.624 |
3.787 |
15 |
0.691 |
1.341 |
2.602 |
3.733 |
20 |
0.687 |
1.325 |
2.528 |
3.552 |
30 |
0.683 |
1.310 |
2.457 |
3.385 |
40 |
0.681 |
1.303 |
2.423 |
3.307 |
60 |
0.679 |
1.296 |
2.390 |
3.232 |
80 |
0.677 |
1.289 |
2.358 |
3.160 |
∞ |
0.674 |
1.282 |
2.326 |
3.090 |
Квантили распределения Стьюдента tp,k
77
Tаблица 3
k |
α = 0.010 |
α = 0.025 |
α = 0.05 |
α = 0.10 |
|
|
|
|
|
1 |
0.00016 |
0.00098 |
0.00393 |
0.01580 |
2 |
0.0201 |
0.05060 |
0.1030 |
0.2110 |
3 |
0.1150 |
0.2160 |
0.3520 |
0.5840 |
4 |
0.297 |
0.484 |
0.711 |
1.106 |
5 |
0.554 |
0.831 |
1.150 |
1.161 |
6 |
0.872 |
1.240 |
1.640 |
2.200 |
7 |
1.240 |
1.690 |
2.170 |
2.830 |
8 |
1.650 |
2.180 |
2.730 |
3.490 |
9 |
2.090 |
2.700 |
3.330 |
4.170 |
10 |
2.560 |
3.250 |
3.940 |
4.870 |
11 |
3.050 |
3.820 |
4.570 |
5.580 |
12 |
3.570 |
4.400 |
5.230 |
6.300 |
13 |
4.110 |
5.010 |
5.890 |
7.040 |
14 |
4.660 |
5.630 |
6.570 |
7.790 |
15 |
5.230 |
6.260 |
7.260 |
8.550 |
16 |
5.81 |
6.91 |
7.96 |
9.31 |
17 |
6.41 |
7.56 |
8.67 |
10.1 |
18 |
7.01 |
8.23 |
9.39 |
10.9 |
19 |
7.63 |
8.91 |
10.1 |
11.7 |
20 |
8.26 |
9.59 |
10.9 |
12.4 |
21 |
8.90 |
10.3 |
11.6 |
13.2 |
22 |
9.54 |
11.0 |
12.3 |
14.0 |
23 |
10.2 |
11.7 |
13.1 |
14.8 |
24 |
10.9 |
12.4 |
13.8 |
15.7 |
25 |
11.5 |
13.1 |
14.6 |
16.5 |
30 |
15.0 |
16.8 |
16.5 |
20.6 |
35 |
18.5 |
20.6 |
22.5 |
24.8 |
40 |
22.2 |
24.4 |
26.5 |
29.1 |
45 |
25.9 |
28.4 |
30.6 |
33.4 |
50 |
29.7 |
32.4 |
34.8 |
37.7 |
75 |
49.5 |
52.9 |
56.1 |
59.8 |
100 |
70.1 |
74.2 |
77.9 |
82.4 |
Квантили распределения χ2α,k
78
|
|
|
|
|
|
Tаблица 4 |
|
|
p = 0.95 |
p = 0.990 |
p = 0.999 |
||||
k2 |
k1 = 1 |
k1 = 2 |
k1 = 1 |
k1 = 2 |
k1 = 1 |
k1 = 2 |
|
1 |
161.4 |
199.5 |
4052 |
4999.5 |
405300 |
500000 |
|
2 |
18.51 |
19.00 |
98.50 |
99.00 |
998.5 |
999 |
|
3 |
10.13 |
9.55 |
34.12 |
30.82 |
167.0 |
148.5 |
|
4 |
7.71 |
6.94 |
21.20 |
18.00 |
74.14 |
61.25 |
|
5 |
6.61 |
5.79 |
16.26 |
13.27 |
47.18 |
37.12 |
|
6 |
5.99 |
5.14 |
13.75 |
10.92 |
35.51 |
27.00 |
|
7 |
5.59 |
4.74 |
12.25 |
9.55 |
29.25 |
21.69 |
|
8 |
5.32 |
4.46 |
11.26 |
8.65 |
25.42 |
18.49 |
|
9 |
5.12 |
4.26 |
10.56 |
8.02 |
22.86 |
16.39 |
|
10 |
4.96 |
4.10 |
10.04 |
7.56 |
21.04 |
14.91 |
|
11 |
4.84 |
3.98 |
9.65 |
7.21 |
19.69 |
13.81 |
|
12 |
4.75 |
3.89 |
9.33 |
6.93 |
18.64 |
12.97 |
|
13 |
4.67 |
3.81 |
9.07 |
6.70 |
17.81 |
12.31 |
|
14 |
4.60 |
3.74 |
8.86 |
6.54 |
17.14 |
11.78 |
|
15 |
4.54 |
3.68 |
8.68 |
6.36 |
16.59 |
11.34 |
|
16 |
4.49 |
3.63 |
8.53 |
6.23 |
16.12 |
10.97 |
|
17 |
4.45 |
3.59 |
8.40 |
6.11 |
15.72 |
10.66 |
|
18 |
4.41 |
3.55 |
8.29 |
6.01 |
15.38 |
10.39 |
|
19 |
4.38 |
3.52 |
8.18 |
5.93 |
15.08 |
10.16 |
|
20 |
4.35 |
3.49 |
8.10 |
5.85 |
14.82 |
9.95 |
|
25 |
4.24 |
3.39 |
7.77 |
5.57 |
13.88 |
9.22 |
|
30 |
4.17 |
3.32 |
7.56 |
5.39 |
13.29 |
8.77 |
|
40 |
4.08 |
3.23 |
7.31 |
5.18 |
12.61 |
8.25 |
|
60 |
4.00 |
3.15 |
7.089 |
4.98 |
11.97 |
7.76 |
|
120 |
3.92 |
3.07 |
6.85 |
4.79 |
11.38 |
7.32 |
|
∞ |
3.84 |
3.00 |
6.63 |
4.61 |
10.83 |
6.91 |
|
Квантили распределения Фишера Fp,k1,k2
79
Tаблица 5
t |
K(t) |
|
|
1.36 |
0.9505 |
1.40 |
0.9603 |
1.45 |
0.9702 |
1.52 |
0.9803 |
1.63 |
0.9902 |
Значения функции распределения Колмогорова K(t)
80
