7.2.Варіаційний ряд та його параметри

Сукупність значень, що вивчаються в даному експерименті або спостереженні параметра, які були ранжовані за величиною (збільшенням або зменшенням), називаються варіаційним рядом.

Припустимо, що ми виміряли артеріальний тиск у десяти пацієнтів із метою отримати верхній поріг АТ: систолічний тиск, тобто тільки одне число.

Уявімо, що серія спостережень (статистична сукупність) артеріального систолічного тиску в 10-и спостереженнях має такий вигляд (табл.1):

Таблиця 1. Незгрупований та неранжований варіаційний ряд

1	2	3	4	5	6	7	8	9	10
120	115	120	125	120	115	120	115	120	120

Щоб отримати варіаційний ряд артеріального тиску, потрібно дану статистичну сукупність розташувати в порядку збільшення або зменшення значень (табл.2):

Таблиця 2. Ранжований варіаційний ряд

1	2	3	4	5	6	7	8	9	10
115	115	115	120	120	120	120	120	120	125

Дані варіаційного ряду називаються варіантами. Варіанти становлять собою числове значення ознаки, що вивчається.

Побудова зі статистичної сукупності спостережень варіаційного ряду – це перший крок до осмислення особливостей усієї сукупності. Потім необхідно визначити середній рівень кількісної ознаки, яка вивчається (середній рівень білка крові, середню вагу пацієнтів, середній час настання наркозу і т.п.).

Середній рівень вимірюють за допомогою критеріїв, які називаються середніми величинами. Середня величина – це узагальнююча числова характеристика якісно однорідних величин, яка характеризує одним числом усю статистичну сукупність по одній ознаці. Середня величина виражає те загальне, що характерне для ознаки в даній сукупності спостережень.

Найчастіше застосовують три види середніх величини: мода (М_о), медіана (М_с), середньоарифметична величина (М).

Для визначення будь-якої середньої величини необхідно використовувати результати індивідуальних спостережень, записавши їх у вигляді варіаційного ряду (табл.2).

Мода – значення, яке найчастіше зустрічається в серії спостережень. У нашому прикладі мода М_о = 120.

Медіана – значення, яке поділяє розподіл на дві рівні частини, центральне або серединне значення серії спостережень, упорядкованих за збільшенням або зменшенням. Якщо у варіаційному ряді 5 значень, тоді його медіана дорівнює третьому члену варіаційного ряду, якщо в ряді парна кількість членів, тоді медіана становить собою середнє арифметичне двох його центральних спостережень, тобто, якщо в ряді 10 спостережень, тоді медіана дорівнює середньому арифметичному 5 і 6 спостережень. У нашому прикладі М_с = (120+120)/2 = 120.

Зауважимо важливу особливість моди і медіани: на їхні величини не впливають числові значення крайніх варіант.

Середня арифметична величина обчислюється за формулою:

М =

де x_i – величина в і-том спостереженні,

n – число спостережень.

Для нашого випадку:

М = (115 + 115 + 115 + 120 + 120 + 120 + 120 + 120 + 120 + 125)/ 10 = 119.

Середня арифметична величина має три властивості:

1. займає серединне положення у варіаційному ряді М = М_о = М_с;

2. вона є узагальнюючою величиною, по середньому арифметичному не видно випадкових коливань, різниць в індивідуальних даних, воно відображає тільки типове, яке характерне для всієї сукупності;

3. сума відхилень усіх варіант від середнього арифметичного дорівнює нулю 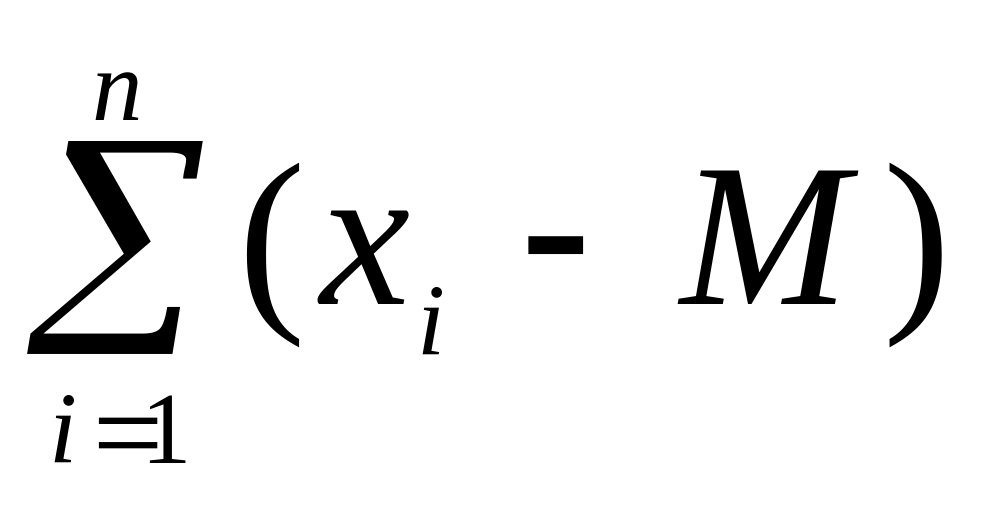= 0. Відхилення варіант від середнього позначається d_i = x_i – M.

Варіаційний ряд складається із варіант і відповідних їм частотам. Із десяти отриманих значень цифра 120 зустрілася 6 разів, 115 – 3 рази, 125 – 1 раз. Частота (р) – абсолютна численність окремих варіант у сукупності, яка вказує, скільки разів зустрічається дана варіанта у варіаційному ряді.

Варіаційний ряд може бути простим (d =1) або згрупованим скороченим, з частотами появи варіант більше одиниці. Простий ряд застосовується за малої кількості спостережень (n≤30), згрупований – за великої кількості числа спостережень (n>30).

Величина однієї й тієї ж ознаки неоднакова у всіх членів сукупності. Наприклад, у групі студентів зріст кожного відрізняється. Саме в цьому проявляється різноманітність параметра, що вивчається. Якщо взяти 3 групи студентів, виміряти їхній зріст і очислити середню арифметичну величину, то для кожної групи студентів отримаємо свою різноманітність ознаки. Статистика дозволяє це охарактеризувати спеціальним критерієм, що визначає рівень різноманітності кожної ознаки в тій або іншій групі.

Найбільш повну характеристику розмаїття ознаки в сукупності дає середнє квадратичне відхилення, σ.

Використовують 2 способи обчислення середнього квадратичного відхилення:

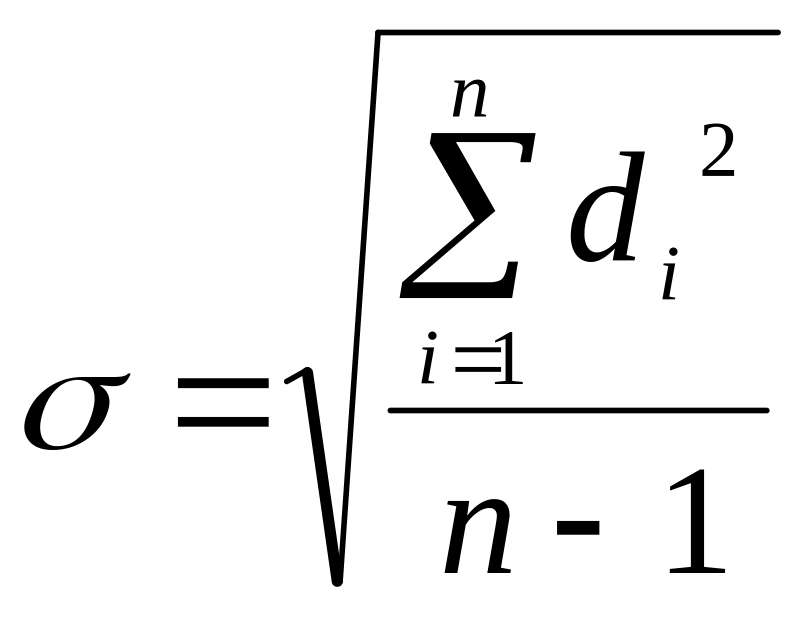; де d_i = x_i – M (1)

Формула (1) використовується за невеликої кількості спостережень (n<30), коли у варіаційному ряді всі частоти р=1.

При р> 1 використовують формулу 2:

(2)

Середнє квадратичне відхилення характеризує ступінь розсіювання варіаційного ряду навколо середньої. Чим менша σ, тім більша типова, точна середня.

Знаючи σ, можна обчислити коефіцієнт варіації Сv (3), необхідний для порівняння ступеня розмаїтості ознак, виражених у різних одиницях вимірювання (сантиметрах, кілограмах та ін.)

(3)

При Сv< 10 спостерігається слабка розмаїтість ознаки, при 10%Сv 20% - середня розмаїтість ознаки, при Сv>20% - сильна розмаїтість ознаки.

Помилка репрезентативності m є найважливішою статистичною величиною, необхідною для оцінки вірогідності результатів дослідження. Ця помилка виникає в тих випадках, коли потрібно по частині охарактеризувати явище в цілому. Ці помилки неминучі. Генеральна сукупність може бути охарактеризована за вибіркою тільки з деякою похибкою, яка вимірюється помилкою репрезентативності. За величиною помилки репрезентативності визначають, наскільки результати, отримані при вибірковому спостереженні, відрізняються від результатів, що могли бути отримані при проведенні дослідження усіх без винятку елементів генеральної сукупності. Це єдиний вид помилок, що не може бути усунутий без переходу на суцільне вивчення генеральної сукупності. Для того, щоб звести помилки репрезентативності до досить малої величини, у вибірці використовується велика кількість спостережень (n).

Кожна середня величина М має бути представлена зі своєю середньою помилкою. Середня помилка середньої арифметичної (помилка репрезентативності) обчислюється за формулою (4):

, при n >30 (4)

, при n <30

Остаточний результат будь-якого дослідження представляється у вигляді M±m.