Симплекс-метод

Графический метод используется только для решения задач с двумя переменными. Для большего числа переменных используется алгебраический симплекс-метод. Процесс носит итерационный характер: вычисления повторяются, пока не будет найдено оптимальное решение.

Нахождение оптимального решения начинается с исходной, допустимой угловой точки (обычно начала координат). Все переходы осуществляются к смежным угловым точкам, каждая из которых предварительно проверяется на оптимальность. Рассмотрим мат. модель, приведенную к стандартной форме, n – количество переменных, m - количество ограничений.

Z = 3 х₁ + 2 х₂ + 0S₁ + 0S₂ + 0S₃ + 0S₄

{	х1 + 2х2 + S1 = 6
	2 х1 + х2 + S2 = 8
	- х1 + х2 + S3 = 1
	х2 + S4 = 2

х₁, х₂ , S₁, S₂, S₃, S₄ ≥ 0

В данном примере n = 6, m = 4, (n - m) = 2

Каждой угловой точке соответствует (n-m) нулевых переменных. Остальные переменные соответственно ненулевые.

	Нулевые переменные	Ненулевые переменные
A B C D E F	х1 х2 S2 х2 S2 S1 S4 S1 S4 S3 S3 х1	S1 S2 S3 S4 S1 х1 S3 S4 х1 х2 S3 S4 х1 х2 S2 S3 х1 х2 S1 S2 х2 S4 S1 S2

Переменные, имеющие нулевые значения, называются небазисными, а остальные – базисные. При переходе от одной угловой точки к другой меняется состав базисных и небазисных переменных.

Включаемой переменной называется небазисная переменная, которая будет включена в базисные на следующей итерации.

Исключаемая переменная – базисная переменная, которая исключается из множества базисных на следующей итерации.

Пусть модель содержит m-уравнений и n неизвестных, тогда (n – m) переменных должны быть равны нулю.

Если базисное решение удовлетворяет требованию неотрицательности правых частей ограничений, оно называется допустимым базисным решением.

Вычислительные процедуры симплекс-метода:

0. определить начальное допустимое базисное решение, приравнивая к нулю (n–m) небазисных переменных.

1. из числа небазисных переменных выбрать включаемую в новый базис переменную увеличение которой обеспечит улучшение значения целевой функции. Если такой переменной нет, то значение оптимально и решение заканчивается, иначе переходим к следующему шагу.

2. из числа переменных текущего базиса выбрать исключаемую переменную.

3. найти новое базисное решение и перейти к шагу 1.

Рассмотрим предыдущий пример: в качестве начального решения используется решение, в котором две (6-4) переменные принимаются, равными нулю. Если взять x1=x2=0, это обеспечит допустимость начального базисного решения: s1=6, s2=8,s3=1,s4=2. Данное решение соответствует точке A(началу координат) на графике. Занесем все данные в симплекс-таблицу.

Симплекс-таблица:

Базовые переменные	x1	x2	S1	S2			S3	S4			Решение
Z S1	-3 1	-2 2	0 1	0 0			0 0	0 0			0 6
S2	2	1	0	1			0	0			8		← ведущая строка
S3 S4	-1 0	1 1	0 0	0 0			1 0	0 1			1 2
	↑ ведущий столбец													S2 - исключаемая х1 – включаемая

Включаемая переменная в задаче max (min) - небазисная переменная являющаяся в Z уравнении наименьшим (наибольшим) коэффициентом; в случае равенства нескольких коэффициентов выбор делается произвольно. Если все коэффициенты неотрицательны (неположительны) – полученное решение есть оптимальное (условие оптимальности).

Условие допустимости: в качестве исключаемой переменной при max (min) выбирается базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к положительному коэффициенту ведущего столбца – минимально, а в случае равенства нескольких отношений выбор делается произвольно.

Поиск нового базисного решения осуществляется по методу Гаусса-Жордана:

• новая ведущая строка = предыдущая ведущая строка / ведущий элемент;

• новое уравнение = предыдущее уравнение – (коэффициент ведущего столбца предыдущего уравнения)*(новая ведущая строка)

Базовые переменные	x1	x2	S1	S2	S3	S4	Решение
Z	0	-1/2	0	3/2	0	0	12
S1	0	3/2	1	-1/2	0	0	2	2:3/2=4/3
Х1	1	1/2	0	1/2	0	0	4	4:1/2=8
S3 S4	0 0	3/2 1	0 0	1/2 0	1 0	0 1	5 2	5:3/2=10/3 2:1=2

Z:

_		-3	-2	0	0	0	0	0
		-3	-3/2	0	-3/2	0	0	-12
		0	-1/2	0	3/2	0	0	12

S₁:

_		1	2	1	0	0	0	6
		1	1/2	0	1/2	0	0	4
		0	3/2	1	-1/2	0	0	2

На следующей итерации – x2 – включаемая, s1 – исключаемая переменные. Итерационный процесс будет продолжаться, пока в z-строке (в задаче max) все переменные не станут положительными.

Анализ математической модели на чувствительность по оптимальной симплекс-таблице.

Из оптимальной симплекс-таблицы можно получить следующую информацию:

• оптимальное решение;

• статус ресурса (дефицитный ресурс или нет);

• ценности ресурса;

• изменение запасов ресурса и коэффициентов целевой функции.

Информация по первым трем пунктам непосредственно берется из симплекс-таблицы; для четвертого пункта требуются дополнительные вычисления.

Базовые переменные	Z	x1	x2	S1	S2	S3	S4	Решение
Z	1	0	0	1/3	4/9	0	0	38/3
Х2	0	0	1	2/3	-1/3	0	0	4/3
Х1	0	1	0	-1/3	2/3	0	0	10/3
S3 S4	0 0	0 0	0 0	-1 -2/3	1 1/3	1 0	0 1	3 2/3

x₁=10/3; x₂=4/3; Z=38/3;

Полученные значения приводятся в столбце решений. Переменные, отсутствующие в столбце базовых переменных, имеют нулевое значение.

Статус ресурса можно установить по значениям остаточных переменных. Положительное значение остаточной переменной указывает на неполное использование исходного ресурса (недефицитный).

S₁ и S₂ – дефицитные ресурсы

S₃ = 3 и S₄ = 2/3 – недефицитные ресурсы

Ценность ресурса характеризуется величиной улучшения оптимального значения Z, приходящегося на единицу прироста объема данного ресурса. Ценности ресурсов определяются по значениям коэффициентов при переменных начального базиса оптимальной симплекс-таблицы.

Несмотря на то, что ценности ресурсов представляются в стоимостном выражении, их нельзя отождествлять с действительными ценами на соответствующие ресурсы. Характеризуют ценность ресурса только относительно полученного оптимального решения.

Для ценности ресурсов используют такие термины, как скрытая цена или двойственная оценка.

Изменение запасов ресурсов:

Предположим, запас первого ресурса составит 6 + ∆₁ тонн. Если выполнить все необходимые вычисления с новым запасом ресурсов для первого ограничения, то в оптимальной симплекс-таблице в столбце решений мы получим следующие значения:

Базовые переменные	Z	x1	x2	S1	S2	S3	S4	Решение
Z	1	0	0	1/3	4/9	0	0	38/3+ ∆1*1/3
Х2	0	0	1	2/3	-1/3	0	0	4/3+∆1*2/3
Х1	0	1	0	-1/3	2/3	0	0	10/3+∆1*(-1/3)
S3 S4	0 0	0 0	0 0	-1 -2/3	1 1/3	1 0	0 1	3 - ∆1 2/3 - ∆1*2/3

Коэффициенты при ∆₁ берутся из столбца S₁, так как S₁ соответствует первому ограничению, для которого мы ищем изменение запаса ресурсов.

∆₁ не может принимать значений, при которых какая-либо из базисных переменных становится отрицательной, то есть должно выполнятся условие неотрицательности правых частей ограничений оптимальной симплекс-таблицы.

{

4/3 + (2/3) ∆1 ≥ 0 10/3 – (1/3) ∆1≥ 0 ; 3- ∆1 ≥0 2/3 – (2/3) ∆1 ≥ 0

{

(2/3) ∆1 ≥ -4/3 (-1/3)∆1 ≥-10/3 ; -∆1 ≥-3 (-2/3) ∆1≥-2/3

{

∆1 ≥ -2 ∆1 ≤ 10 ∆1 ≤ 3 ∆1 ≤ 1

-2 ≤ ∆₁ ≤ 1

6 – 2 = 4 тонн – min запас 1 ресурса

6 + 1 = 7 тонн – max запас 1 ресурса

Любое значение ∆₁ выходящее за пределы указанного интервала, приведет к недопустимости решения и новой совокупности базовых переменных.

Значение Z изменяется по формуле 38/3+(1/3) ∆₁ и при ∆₁=1 Z=13 тысяч ден. ед.

∆₂ : 38/3 + (4/3) ∆₂

{	4/3 – (1/3) ∆2 ≥ 0 10/3 + (2/3) ∆2 ≥ 0 3 + ∆2 ≥ 0 2/3 + (1/3) ∆2 ≥ 0

Диапазон изменения коэффициентов целевой функции:

Предположим, что коэффициент при х₁ изменится на (3+∂₁), то Z = 3+∂₁)х₁+2х₂.

Если провести все необходимые вычисления до получения оптимальной симплекс-таблицы, то последнее Z уравнение будет таким:

	x1	x2	S1	S2	S3	S4	Решение
Z	0	0	1/3-(1/3) ∂1	4/3+(2/3) ∂1	0	0	38/3+ (10/3) ∂1

Коэффициенты при ∂₁ равны коэффициентам при соответствующих переменных в х₁ уравнении симплекс-таблицы.

{	1/3 – (1/3) ∂1 ≥ 0	Для максимизации: ≥
	4/3 + (2/3) ∂1 ≥ 0 ;	Для минимизации: ≤

{	∂1 ≤ 1
	∂1 ≥ -2 ;

3-2=1 – min значение коэффициента

3+1=4 – max значение коэффициента

При 1 ≤ С₁ ≤ 4 оптимальные значения переменных остаются неизменными

Для S₂ : 38/3+ (4/3) ∂₂

{	1/3 + (2/3) ∂2 ≥ 0
	4/3 - (1/3) ∂2 ≥ 0 ;

{	∂2 ≥ -1/2
	∂2 ≤ 4 ;

Искусственное начальное решение. М-метод. Двухэтапный метод.

Если ограничения модели имеют знаки ≤, то начальное допустимое базисное решение состоит из остаточных переменных, если же в ограничениях присутствуют знаки ≥ или = , нельзя сразу же получить допустимое базисное решение решение.

Пример: min Z = 4 х₁ + х₂

{	3х1 + х2 = 3
	4х1 + 3х2 ≥ 6
	х1 + 2х2 ≤4

х₁, х₂ ≥ 0

{	3х1 + х2 = 3
	4х1 + 3х2 - х3 = 6
	х1 + 2х2 + х4 = 4

х₁, х₂ , х₃, х₄ ≥ 0

В данной ситуации нельзя быть уверенным в том, что при нулевом значении какой-либо переменной, все базисные переменные будут неотрицательными, поэтому вводятся искусственные переменные, которые выполняют роль остаточных в ограничениях со знаком ≥ или =. Эти переменные необходимы только для получения стартовой точки, в конечном оптимальном решении они должны принимать нулевые значения.

Существует два метода с использованием искусственных переменных:

1. М-метод (метод больших штрафов);

2. двухэтапный метод

М-Метод

R₁, R₂ – искусственные переменные, вводятся только в те ограничения, в которых нет остаточных переменных, т.е. имеющие знаки >=, =.

{	3х1 + х2 + R1 = 3
	4х1 + 3х2 - х3 + R2= 6
	х1 + 2х2 + х4 = 4

х₁, х₂ , х₃, х_{4 ,} R₁, R₂ ≥ 0

6-3=3

х₁, х₂ , х₃ =0; х₄ = 4; R₁= 3; R₂ = 6 – начальное допустимое базисное решение.

За использование искусственной переменной в составе целевой функции вводится «штраф»: достаточно большой положительный коэффициент М в задаче min и достаточно большой по абсолютному значению отрицательный коэффициент в задаче max.

Z = 4х₁ + х₂ + M R₁ + M R₂

Так как М достаточно большое положительное число, то в задаче минимизации, в оптимальном решении, переменные R1 и R2 обратятся в ноль.

Если решается задача максимизации, то этим переменным в целевой функции приписывается большой по абсолютной величине отрицательный коэффициент.

Так как в целевой функции присутствуют базисные переменные R₁ и R₂ , их необходимо выразить через небазисные переменные , то есть из 1-го и2-го ограничений, и подставить в целевую функцию.

R₁ =3 - 3х₁ - х₂

R₂= 6 - 4х₁ - 3х₂ + х₃

Z = 4х₁ + х₂ + M (3 - 3х₁ - х₂) + M (6 - 4х₁ - 3х₂ + х₃) = (4 - 7M) х₁ + (1 – 4M) х₂ + + Mх₃+ 9M

Z - (4 - 7M) х₁ - (1 – 4M) х₂ - Mх₃ = 9M

Z+(-4+7M)x1+(-1+4M)x2-Mx3=9M

Итерация 0:

Баз. Пер.	х1	х2	х3	R1	R2	х4	Решение
Z	7 М - 4	4 М - 1	- М	0	0	0	9 М
R1	3	1	0	1	0	0	3
R2	4	3	-1	0	1	0	6
х4	1	2	0	0	0	1	4

Итерация 3 - Оптимальная таблица:

Баз. Пер.	х1	х2	х3	R1	R2	х4	Решение
Z	0	0	0	7/5 – М	- М	-1/5	17/5
х1	1	0	0	2/5	0	-1/5	2/5
х2	0	1	0	-1/5	0	3/5	9/5
х3	0	0	1	1	-1	1	1

х₁ = 2/5 ; х₂ = 9/5 ; x3=1; Z = 17/5 Значения R1, R2=0

В оптимальном решении искусственные переменные имеют нулевое значение. Если хотя бы одна искусственная переменная имеет положительное значение в оптимальном решении – решение недопустимо.

Недостаток М-метода заключается в том, что из-за больших коэффициентов М процесс вычисления может стать нечувствительным к значениям исходных коэффициентов.

Двухэтапный метод (не использует коэффициентов М)

1 этап: Вводятся искусственные переменные, записывается новая целевая функция, соответствующая минимизации суммы искусственных переменных. Задача решается симплекс-методом. Если полученное минимизированное решение новой целевой функции равно нулю, то исходная задача имеет допустимое решение. Переход к этапу 2. Если на первом этапе значение целевой функции не равно 0, то исходное задача не имеет допустимых решений, процесс вычисления заканчивается.

2 этап: полученное оптимальное решение на первом этапе используется в качестве начального решения на втором этапе при исходной целевой функции.

Рассмотрим тот же пример и решим двухэтапным методом.

min Z = 4 х₁ + х₂

{	3х1 + х2 + R1 = 3
	4х1 + 3х2 - х3 + R2= 6
	х1 + 2х2 + х4 = 4

х₁, х₂ , х₃ =0; х₄ = 4; R₁= 3; R₂ = 6 – начальное допустимое базисное решение.

I этап:

r = R₁+ R₂

{	3х1 + х2 + R1 = 3
	4х1 + 3х2 - х3 + R2= 6
	х1 + 2х2 + х4 = 4

Т.к. в состав целевой функции входят базисные переменные, выразим базисные переменные через небазисные и подставим в целевую функцию.

r = R₁ + R₂ = 3 - 3х₁ - х₂ + 6 - 4х₁ - 3х₂ + х₃ = - 7х₁ - 4х₂ + х₃ + 9

r + 7х₁ + 4х₂ - х₃ = 9

итерация 0:

Баз. Пер.	Х1	х2	х3	R1	R2	х4	Решение
r	7	4	- 1	0	0	0	9
R1	3	1	0	1	0	0	3
R2	4	3	-1	0	1	0	6
х4	1	2	0	0	0	1	4

Оптимальная таблица:

Баз. Пер.	Х1	х2	х3	R1	R2	х4	Решение
r	0	0	0	-1	-1	0	0
R1	1	0	1/5	3/5	-1/5	0	3/5
R2	0	1	-3/5	-4/5	3/5	0	6/5
х4	0	0	1	1	-1	1	1

Так как r=0, то переходим к этапу 2.

Этап II:

Min Z = 4x₁+ x₂

{	х1 + (1/5)х3 = 3/5
	х2 – (3/5)х3 = 6/5
	х3 + х4 = 1

х₁, х₂, х_3, х₄ ≥ 0

4 - 3=1, если

х₃ = 0, то х₁ = 3/5, х₂ = 6/5, х₄ = 1 – начальное допустимое базисное решение

Выразим базисные переменные через небазисные:

х₁ =3/5 – (1/5) х₃

х₂= 6/5 + (3/5)х₃

Z = 4 ( 3/5 – (1/5) х₃ ) + ( 6/5 + (3/5) х₃ ) = (-1/5) х₃ + 18/5

Z + (1/5) х₃ = 18/5

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	0	0	1/5	0	18/5
х1	1	0	1/5	0	3/5
х2	0	1	-3/5	0	6/5
х4	0	0	1	1	1

Оптимальную таблицу получим на следующей итерации:

х₁ = 2/5, х₂ = 9/5, Z = 17/5

Количество итераций в м-методе и в двухэтапном методе всегда одинаковы, и между таблицами имеется взаимнооднозначное соответствие.

Рассмотрим примеры:

Необходимо ли использование искусственных переменных для получения начального решения в следующих задачах?

1. Max z=x1+x2

2 x1+3x2=5

7x1+2x2<=6

x1,x2>=0

2.min z=x1+x2+x3+x4

2x1+x2+x3=7

4x1+8x2+x4=8

X1,x2,x3,x4>=0

Особые случаи применения симплекс-метода

1. Вырожденность

2. Альтернативное оптимальное решение

3. Неограниченные решения

4. Отсутствие допустимых решений

Вырожденность

Если по условию допустимости любая переменная может быть исключена из базиса и выбор делается произвольно, то на следующей итерации, по крайней мере, одна из базисных переменных становится равной нулю. В этом случае говорят, что решение является вырожденным.

С практической точки зрения данная ситуация объясняется наличием в модели избыточных ограничений.

Пример: max Z = 3 х₁ + 9х₂

{	х1 + 4 х2 ≤ 8 - (1) х1 + 2 х2 ≤ 4 - (2)

x₁ , x ₂ ≥ 0

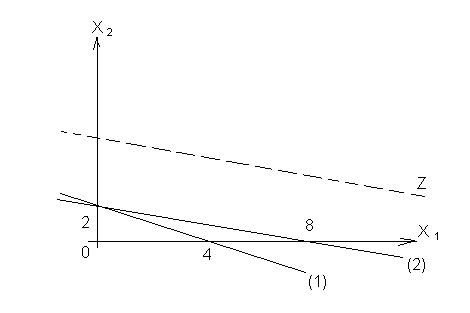
0 итерация:

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	- 3	- 9	0	0	0
х3	1	4	1	0	8
х4	1	2	0	1	4

1 итерация

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	- 3/4	0	9/4	0	18
х2	1/4	1	1/4	0	2
х4	1/2	0	-1/2	1	0

2 итерация

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	0	0	3/2	3/2	18
х2	0	1	1/2	-1/2	2
Х1	1	0	-1	2	0

На 1 и 2 итерациях хотя состав базисных и небазисных переменных

Вырожденность может приводить к зацикливанию процесса вычислений, но вероятность зацикливания мала, поэтому особых методов предотвращающих это явление, не существует.

Итерации симплекс-метода должны выполнятся до тех пор, пока результаты не будут удовлетворять условиям оптимальности, так как вырожденное решение может быть промежуточным.

Альтернативное оптимальное решение

Если прямая или плоскость, представляющая собой целевую функцию, параллельна прямой или плоскости, соответствующей связующему ограничению, целевая функция принимает одно и тоже оптимальное решение в нескольких точках пространства решений. Такие решения называются альтернативными.

Пример: max Z = 2 х₁ + 4 х₂

{	х1 + 2 х2 ≤ 5 - (1) х1 + х2 ≤ 4 - (2)

x₁ , x ₂ ≥ 0

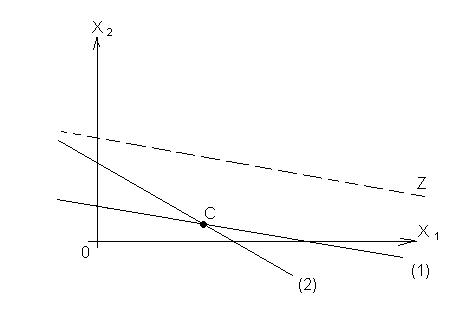
Альтернативное решение - можно определить при нулевых значениях коэффициентов, при небазисных переменных в Z.

0 итерация:

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	- 2	- 4	0	0	0
х3	1	2	1	0	5
х4	1	1	0	1	4

1 итерация:

Баз. Пер.	Х1	х2	х3	х4	Решение
Z	0	0	2	0	10
х2	½	0	½	0	5/2
х4	1/2	0	- ½	1	3/2

Z = 10; x₂ = 5/2; x ₄ = 3/2;

Z = 10; x₁ = 3; x ₂ = 1;

Информация о наличии альтернативных решений может быть полезной при решении практических задач, так как существует возможность выбора альтернативного решения в большей степени отвечающего сложившийся ситуации.

Неограниченные решения

Некоторые задачи могут допускать бесконечное увеличение значений переменных без нарушения наложенных ограничений. Это говорит о том, что модель недостаточно точна:

• Не учтены одно или несколько ограничений, не являющихся избыточными;

• Не точно оценены параметры ограничений.

_{Пример: max Z = 2 х1 + х}2

{	х1 - х2 ≤ 10 - (1) 2 х1 ≤ 40 - (2)

x₁ , x ₂ ≥ 0

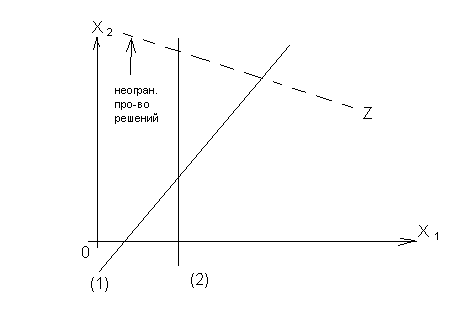
Баз. Пер.	Х1	х2	х3	х4	Решение
Z	- 2	- 1	0	0	0
х3	1	- 1	1	0	10
х4	2	0	0	1	40

Если на некоторой итерации небазисная переменная имеет в ограничениях не положительные коэффициенты, то пространство решений, в данном направлении, не ограничено.

Если, кроме того,: коэффициент при это переменной в Z уравнении отрицателен (в задаче max) или положителен (в задаче min), то целевая функция так же не ограничена.

_{Пример: max Z = 6 х1 - 2 х}2

{	2 х1 - х2 ≤ 2 - (1) х1 ≤ 4 - (2)

x₁ , x ₂ ≥ 0

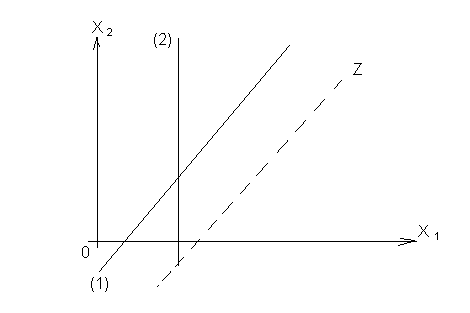
Баз. Пер.	Х1	х2	х3	х4	Решение
Z	- 6	2	0	0	0
х3	2	- 1	1	0	2
х4	1	0	0	1	4

Отсутствие допустимых решений