Модели на сетях (графах). Теория графов.

Графом называется пара G=(V,E). Элементы множества V называются вершинами графа, элементы множества Е - ребрами или дугами. Если множество Е состоит только из ребер, то граф называется неориентированным, если только из дуг, то ориентированным или орграфом. Если в Е есть и ребра и дуги, то граф называется смешанным. Контур или цикл – это замкнутый маршрут, где V₁=Vn. Последовательность различных дуг или ребер, где V1<>Vn, представляют путь или цепь соответственно. Граф называется взвешенным, если его ребрам приписаны числа, называемые весами. Длиной пути называется сумма весов, входящих в него дуг или ребер. С помощью графов можно решить следующие задачи:

Проектирование газопровода, имеющего минимальную стоимость; определение кратчайшего пути между двумя города в сети шоссейных дорог; определение максимальной пропускной способности трубопровода и так далее. Оптимизационные задачи на графах можно описать четырьмя типами моделей:

• минимизация сети

• нахождение кратчайшего маршрута

• Определение максимального потока

• минимизация стоимости потока в сети с ограниченными пропускными способностями коммуникаций

Рассмотренные модели связаны с определением расстояний и материальных потоков.

Минимизация сети

Данная задача состоит в нахождении ребер, соединяющих все узлы графа и имеющих минимальную длину. В итоге должны получить минимальное дерево-остов, граф, в котором отсутствуют циклы.

Алгоритм :

• начать с любого узла графа, соединить его с ближайшим узлом. Соединенные узлы образуют связное множество, остальные – несвязное.

• В несвязном множестве выбрать узел, который расположен ближе других к любому из узлов связного множества.

• Скорректировать связное и несвязное множества.

• Повторять до тех пор, пока в связное множество не попадут все узлы сети.

Рассмотрим задачу: телевизионная фирма планирует создание кабельной сети для обслуживания пяти районов-новостроек. Числа на ребрах указывают длину кабеля. Узел 1 представляет телевизионный центр, а остальные - районы-новостройки. Нужно найти такие ребра, которые потребуют кабель минимальной длины для связи (прямой или через другие пункты) всех районов с телевизионным центром.

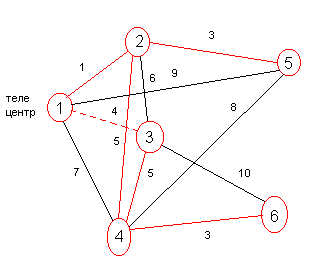
0. C = {1} и Ĉ = {2,3,4,5,6}

1. C = {1,2}

2. C = {1,2,5}

3. C = {1,2,4,5}

4. C = {1,2,4,5,6}

5. C = {1,2,3,4,5,6}

Минимальная длина кабеля: Z = 1 + 3 + 4 + 3 + 5 = 16

Алгоритм нахождения кратчайшего пути для сетей без циклов

В основе лежит схема рекуррентных вычислений.

Где d_ij - расстояние между узлами i и j, а U_j – кратчайшее расстояние между 1 и j (U₁=0)

U_j = min {U_i + d_ij}

i

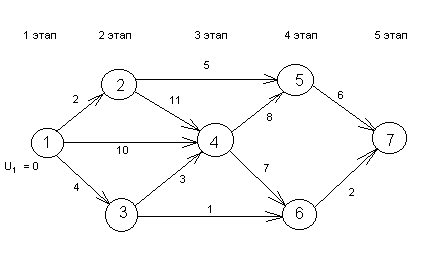
1 этап: U₁ = 0;

2 этап: U₂ = U₁ + d₁₂ = 0 + 2 = 2 (из 1) и U₃ = U₁ + d₁₃ = 0 + 4 = 4 (из 1)

3 этап: U₄ = min {U₁ + d₁₄ ; U₂ + d₂₄ ; U₃ + d₃₄ } = min {10;13;7} = 7 (из 3)

4 этап: U₅ = min {U₂ + d₂₅ ; U₄ + d₄₅ } = min {7;15} = 7 (из 2)

U₆ = min {U₃ + d₃₆ ; U₄ + d₄₆ } = min {5;14} = 5 (из 3)

5 этап: U₇ = min {U₅ + d₅₇ ; U₆ + d₆₇ } = min {13;7} = 7 (из 6)

Тогда путь: 1 → 3 → 6 → 7