Представление задачи о кратчайшем пути в виде транспортной задачи с промежуточными пунктами.

Задачу о кратчайшем пути можно представить как транспортную задачу с промежуточными пунктами. Рассмотрим сеть с одним исходным пунктом и одним пунктом назначения. Величина предложения в исходном пункте и величина спроса в пункте назначения равны 1, т.е. единица груза транспортируется из исходного пункта в пункт назначения по маршруту, имеющему минимальную длину пути. Емкость В равна 1, узлы 1 и 7 не могут рассматриваться в качестве промежуточных. «Стоимости перевозок» полагаются равными соответствующим расстояниям. Если маршрута не существует, стоимость берется завышенной - М.

15	1 11	М	1
М	4	1 1	0+В
1 1	М		0+В
0+В	0+В	1

Кратчайший путь: 1-3-2-4, кратчайшее расстояние :z=11+1+1=13.

Данную задачу можно представить как задачу линейного программирования:

M in z=

- из исходного пункта

- для промежуточных пунктов

- в пункт назначения

Xij=0 или 1.

Xij представляет величину потока по дуге (i , j) . Суммарный поток, выходящий из узла 1 равен 1(1 ограничение), как и суммарный поток, входящий в пункт n (последнее ограничение модели). В любом промежуточном узле суммарный входящий поток равен суммарному выходящему потоку. Целевая функция требует, чтобы расстояние, пройденное единицей потока было минимальным. Переменная xij может принимать значения, равные 0 или 1. Если xij=1, то дуга принадлежит кратчайшему пути, если xij=0, то дуга не принадлежит кратчайшему пути. Составим целевую функцию и ограничения для примера, рассмотренного ранее:

Min z=15x₁₂+11x₁₃+3x₂₁+4x₂₃+x₂₄+8x₃₁+x₃₂+5x₃₄+100x₄₂+3x₄₃

П ри ограничениях:

x₁₂+x₁₃=1

x₁₂+x₃₂+x₄₂=x₂₁+x₂₃+x₂₄

x₁₃+x₂₃+x₄₃=x₃₁+x₃₂+x₃₄

x₂₄+x₃₄=1

Тема: Максимальный поток Алгоритм определения максимального потока

1. Найти цепь соединения S с t, по которой поток принимает положительное значение (>0) . Если такой цепи нет, то перейти к 3.

2. С_ij ^-- (С_ij ⁺) – S → t (t → S) и Θ = min { С_ij ^-} > 0

Скорректировать матрицу пропускных способностей. Вычесть Θ из всех С_ij ^-- и прибавить к Θ ко всем С_ij ⁺. Перейти к пункту 1. Данные операции дают возможность использовать остатки пропускных способностей от S к t и восстановить исходные пропускные способности , так как уменьшение пропускной способности дуги в одном направлении можно рассматривать как увеличение ее пропускной способности в обратном направлении.

3. Найти максимальный поток в сети.

Пусть С = ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌║ С_ij ║ - исходная матрица, а С*=║ С*_ij║ - полученная матрица

Тогда матрица максимального потока х = ║ х_ij ║ :

хij ={

Сij - Сij *, если Сij > Сij * 0, если Сij < Сij *

Z = Σ х_sj = Σ х_jt = Σ Θ

i j

Рассмотрим пример.

Каждая дуга сети обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего по данной дуге. Односторонняя дуга соответствует нулевой пропускной способности в запрещенном направлении. Пропускные способности С_ij представляются в виде матрицы.

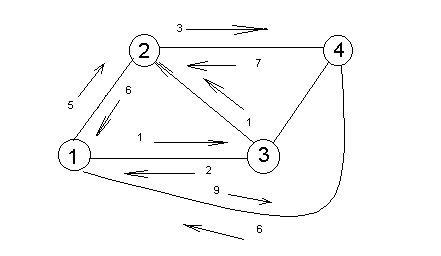
С:

	1	2	3	4
1		_ 5	1	9
2	+ 6		0	_ 3
3	2	1		5
4	6	+ 7	6

1 → 2 → 4

S → t

12 и 24 - « - »

21 и 42 – « + »

min {5,3} = 3 (знак «-»)

Θ = 3

Ячейка 30 – знак «-» - вычитаем Θ, если же знак «+», то прибавляем Θ

Из 1 в 4:

	1	2	3	4
1		2	_ 1	9
2	9		0	0
3	+ 2	1		_ 5
4	6	10	+ 6

1 → 3 → 4

Θ = 1

	1	2	3	4
1		2	0	_ 9
2	9		0	0
3	3	1		4
4	+ 6	10	7

1 → 4

Θ = 9

С*:

	1	2	3	4
1		2	0	0
2	9		0	0
3	3	1		4
4	15	10	7

Положительных потоков больше нет.

Х = {0, если С_ij – С*_ij <0}

С_ij – С*_{ij, иначе}

Х:

	1	2	3	4
1		3	1	9
2	0		0	3
3	0	0		1
4	0	0	0

9 + 3 +1 = 13

Z = Θ

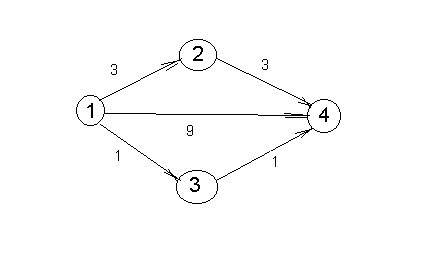
Задачу о максимальном потоке можно рассмотреть как задачу ЛП. Пусть y - поток из источника 1 в сток n. Обозначим поток по дуге (i,j) через xij, получим следующую модель:

Max z=y

- источник

, для всех k<> 1 или n

- сток

0≤xij≤uij, для всех i,j. Uij – пропускная способность дуги (i,j)

Для рассматриваемого примера: z=y

x ₁₂+x₁₃+x₁₄=y

x₂₁+x₂₄+x₁₂+x₃₂+x₄₂

x₁₃+x₂₃+x₄₃=x₃₁+x₃₄

x₁₄+x₂₄+x₃₄=y