Вопросы для повторения

1. Какое движение твердого тела называется плоскопарал-лельным?

2. Какими уравнениями задается плоскопараллельное дви-жение?

3. Зависят ли поступательное перемещение плоской фигу-ры и ее вращение от выбора полюса?

4. Как по уравнениям движения плоской фигуры найти скорость полюса и угловую скорость?

5. Как связаны между собой скорость произвольной точки плоской фигуры и скорость ее точки, принятой за полюс?

6. Чему равна и как направлена скорость в равенстве ?

7. Какая из точек А и В плоской фигуры имеет большую скорость, если угол между и прямой АВ равен 45°, а угол между и прямой АВ равен 15°?

8. Что называется мгновенным центром скоростей плоской фигуры и как он определяется в различных случаях?

9. Где находится мгновенный центр скоростей плоской фигуры, совершающей мгновенно поступательное движение?

10. Каков закон распределения скоростей точек плоской фигуры относительно ее мгновенного центра скоростей?

11. Какая точка колеса, катящегося без скольжения по неподвижной поверхности, имеет наибольшую скорость?

12. Как направлена скорость точки В плоской фигуры относительно прямой АВ, если скорость точки А перпенди-кулярна этой прямой?

13. Чему равна скорость точки В плоской фигуры, если скорость вращения этой точки вокруг полюса А векторно равна скорости точки А?

3.4.8. Теорема об ускорениях точек плоской фигуры и ее следствия

Ускорения точек плоской фигуры определяются следующей теоремой: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении вокруг полюса.

Для установления этой зависимости допустим, что известно ускорение некоторой точки А плоской фигуры и алгебраические величины угловой скорости ω, углового ускорения ε фигуры, известны так же в данный момент направление вращения плоской фигуры и характер ее вращения (ускоренное или замедленное).

Пусть в данный момент времени фигура вращается ускоренно в сторону, противоположную движению часо-вой стрелки (рис. 3.29). Определим ускорение точки В фигуры, приняв точку А за полюс.

Воспользуемся теоремой о сложении скоростей фигу-ры, приняв точку А за полюс. На основании (3.30) имеем

.

Ускорение точки А найдем как векторную производ-ную по времени от скорости этой точки:

,

где , ,

Тогда

. (3.36)

Здесь - вращательное (касательное) ускорение точки В вокруг точки А направлено перпендикулярно АВ соответственно направлению .

- центростремительное (нормальное) ускорение точки В вокруг точки А направлено к полюсу А по АВ. Но геометрическая сумма касательного и нормального ускорений является полным ускорением точки В во вращении вокруг полюса А, поэтому

. (3.37)

При этом для ускорения точки В во вращатель-ном движении вокруг полюса А по формулам (3.12-3.14) (см. п.3.3) будет

, ;

или

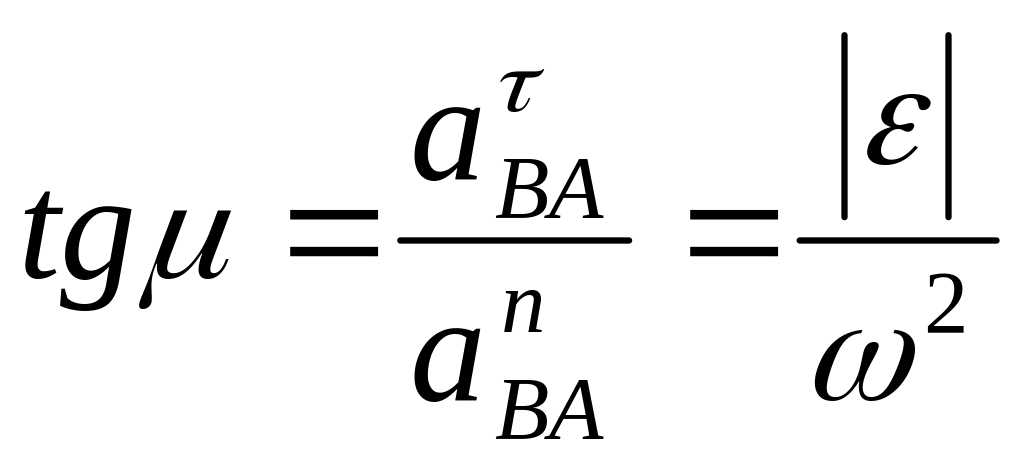; . (3.38)

Здесь ω и ε – угловая скорость и угловое ускорение тела, а μ – угол между направлением и отрезком АВ.

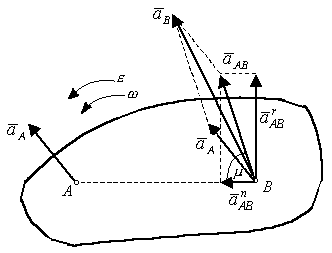
Рис. 3.29

У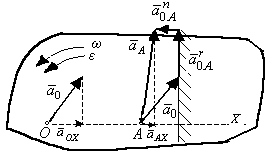 скорение точки В плоской фигуры определяется путем построения многоугольника ускорений. На рис. 3.29 построен прямоугольник, определяющий ускорение точки В в ее вращательном движении вокруг полюса А: , а затем находится ускорение , как диагональ па-раллелограмма ускоре-ний, сторонами которо-го служат ускорение полюса и ускорение

Рис 3.30 точки во вращательном движении вокруг полюса .

Следствие 1. Проекция ускорения любой точки плос-кой фигуры на ось, проведенную из произвольного полюса через эту точку, не может быть больше проекции ускорения полюса на эту же ось.

Доказательство. Ускорение точки А плоской фигуры определяется по формуле (3.37):

.

Сложим векторы и по правилу много-угольника, тогда будет замыкающей стороной много-угольника ускорений (рис. 3.30). Проведем из полюса О через точку А ось Х и спроектируем все векторы на эту ось:

.

Проекция нормального ускорения на ось Х всегда отрицательна, так как это ускорение направлено от точки А к полюсу О, то есть противоположно направлению оси Х: . Проекция касательной составляющей ускорения на ось Х равна нулю, так как это ускорение всегда перпендикулярно оси Х: . На этом основании находим, что , следовательно

,

что и требовалось доказать.

Следствие 2. Концы векторов ускорений точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между этими точками. (Примем без доказательства см. [1-5]).

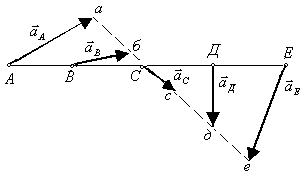
Этим следствием удобно пользоваться при решении задач графическим способом. Допустим, что требуется определить ускорения точек Д, С и Е, делящих отрезок на четыре равные части (рис. 3.31). Соединяем концы ускорений точек А и Е, отложенных в масштабе, отрез-ком прямой ае и делим этот отрезок точками б, с и д на четыре равные части. Соединяя точки В и б, С и с, Д и д, получаем уско-рения этих точек и . Поль-

зуясь масштабом, находим их модули и по чертежу определяем их нап-равления.

Рис. 3.31

Если полюс движется непрямолинейно, то его уско-рение также слагается из касательного и нормального ускорений, и тогда

. (3.39)

Формулами (3.38) и (3.39) пользуются при решении задач, вычисляя векторы, стоящие в правой части равен-ства, а затем определяя их геометрическую сумму или произведя соответствующее графическое построение. Вектор можно найти по правилу параллелограмма , а затем по правилу параллелограмма найти ускорение точки А: . Однако, вычис-ление с помощью параллелограмма усложняет расчет, так как сначала нужно определить угол , а затем угол между векторами . Поэтому при решении задач удобнее вектор заменить его и составляющими: нормального ускорения , направленного по АВ к полюсу В, и касательного ускорения , направленного перпендикулярно АВ в сторону вращения, если движение ускоренное и против, если движение замедленное.