3.4.3. Независимость угловой скорости фигуры от выбора полюса

Основными кинематическими характеристиками рас-сматриваемого ППД являются скорость и ускорение поступательного движения, а также угловая скорость ω и угловое ускорение ε вращательного движения тела вокруг полюса.

Очевидно, что характеристики поступательной части плоского движения, такие как перемещение, скорость и ускорение зависят от выбора полюса, а за полюс можно брать любую точку тела. Например, если за полюс взять точку С, то характеристики поступательного движения будут соответственно . Если бы а , то движение тела было бы поступательным, так как при равенстве в каждый момент времени перемеще-ний, скоростей и ускорений хотя бы двух точек плоской фигуры, последняя совершала бы поступательное движение.

Характеристики вращательной части плоского движе-ния, то есть угловая скорость ω и ускорение ε, остаются неизменными, независящими от выбора полюса. Докажем это.

Возьмем в сечении S (рис. 3.15) две параллельные прямые АВ и СД. Если за полюс взять точку А, то угол поворота отрезка АВ относительно оси Ох равен φ₁. Если за полюс взять точку С, то угол поворота отрезка СД бу-дет равен φ₂. А так как произвольно выбранные отрезки АВ и СД параллельны, то , то есть законы вращения вокруг полюсов одинаковы, отсюда:

, или ω₁ = ω₂ = ω;

, или , что

Рис. 3.15 и требовалось доказать.

3.4.4. Определение траектории точек тела

Рассмотрим точку М тела, положение которой в сечении S определяется расстоянием АМ от полюса А и углом (рис. 3.16). Если движение тела задано уравнениями (3.24), то координаты х и у точки М в осях Охуz будут:

, (3.25)

г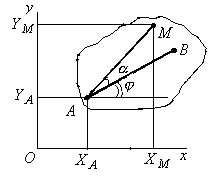 де Х_А, Y_А, φ – известные по уравнениям (3.24) функции времени t.

Равенства (3.25) опреде-ляют закон движения точки М в плоскости Оху, дают одновременно уравнение траектории этой точки в параметрическом виде.

Рис. 3.16 Уравнение траектории в

обычном виде можно получить из (3.25) решив их сов-местно, исключив из системы уравнений время t.

3.4.5. Определение скоростей точек тела

Угловую скорость и угловое ускорение при плоском движении твердого тела можно представить в виде векторов, расположенных вдоль подвижной оси, перпендикулярной плоскости движения и проходящей через выбранный полюс (рис. 3.17). Вектор угловой скорости направлен в ту сторону, откуда мы видим вращение тела, происходящим против хода часовой стрелки. Его модуль равен

. (3.26)

При ускоренном вращении вектор углового ускорения направлен в ту же сторону, что и вектор угловой скорости , при замедленном - в противоположную. Его модуль равен

Рис. 3.17 . (3.27)

Перейдем теперь к изучению движения отдельных точек тела, то есть к изучению их траекторий, скоростей и ускорений.

Дифференцированием по времени уравнений плоскопараллельного движения (3.24) определяются только скорость полюса А и угловая скорость тела:

, , , . (3.28)

Чтобы при помощи этих уравнений определить ско-рость любой точки плоской фигуры, рассмотрим движе-ние ее произвольной точки В (рис. 3.18), положение которой в каждый момент времени по отношению к неподвижной системе отсчета Oxyz определяется радиус-вектором

, (3.29)

г де - радиус-вектор полюса А, а - радиус-вектор точки В, - радиус-вектор точки В относительно полюса А. Вектор является вектором постоянного модуля, так как расстояние между точками А и В твердого тела в процессе движения остается неизмен-ным; этот вектор вращается вместе с телом вокруг подвижной оси, перпен-дикулярной плоскости движения фигуры, с угловой скоростью ω.

Взяв производную по времени

Рис. 3.18 от последнего равенства, получим

.

В этом выражении - скорость полюса А. Производная вектора постоянного модуля по времени определяется по формуле Эйлера и обозначается как :

.

В соответствии с правилом векторного произведения вектор лежит в плоскости фигуры. Он перпендикуля-рен отрезку АВ и направлен в сторону вращения плоской фигуры. Модуль вектора равен

.

Вектор определяет скорость точки В, которую эта точка имела бы при неподвижном полюсе А, то есть при вращении фигуры вокруг неподвижной оси с угловой скоростью ω. Окончательно, для определения скорости произвольной точки плоской фигуры получаем формулу

, (3.30)

где

, (3.31)

Таким образом, мы доказали теорему о сложении скоростей: скорость любой точки тела при его плоско-параллельном движении равна векторной сумме скоро-сти полюса и скорости данной точки при ее вращении вместе с телом вокруг полюса.

Н аправление и величина находится по правилу параллело-граммма (рис. 3.19). Для этого по формулам (3.28) находят скорость полюса и угловую скорость тела ω. Затем по формулам (3.31) опре-

Рис. 3.19 деляют скорость . Откладывая из точки В по величине и направлению векторы скорос-тей и строят параллелограмм для определения величины и направления искомой скорости .

Следствие 1. Проекции скоростей двух точек на прямую, соединяющую эти точки равны друг другу.

Докажем это. Рассмотрим какие-нибудь две точки А и М твердого тела его в ППД (рис. 3.20, а).

Рис. 3.20

Принимая точку А за полюс и используя теорему о сложении скоростей (3.30), запишем: . Проектируя это уравнение на ось (рис. 3.20, а), получим , так как . Этот результат позволяет легко находить скорость точки тела, если известны направление движения этой точки и величина и направление скорости какой-нибудь точки того же тела.

Следствие 2. Концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка (рис. 3.20, б, в). Примем без доказательства (см. [1.-5]).