3.4.7. Мгновенный центр скоростей
Точка плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).
Покажем, что если угловая скорость
плоской фигуры не равна нулю (ω ≠
0), то такая точка существует. Дейст-вительно,
пусть в данный момент скорость точки А
фигуры равна
и фигура вращается с угловой ско-ростью
ω. Проведем луч АN,
перпендикулярный вектору
,
в направлении, соответствующем направлению
вращения (рис. 3.23). Отложим на этом луче
отрезок
и определим скорость полученной точки
Р, выбрав за полюс точку А:
,
где
.
Так как вектор
перпендикулярен АР и направлен в
сторону вращения фигуры, то
.
Тогда
,
то есть точка Р фигуры являет-ся в
данный момент времени ее МЦС, что и
требовалось доказать. Очевидно, что эта
точка единственная. При наличии второй
точки с нулевой скоростью, фигура в
данный момент была бы неподвижна и
скорости всех ее точек равнялись бы
нулю, что противоречит исходным
предпосылкам.
Рис. 3.23 Рис. 3.24
Если положение МЦС в данный момент времени известно, то, приняв его за полюс, получим следующие выражения для определения скоростей точек плоской фигуры (рис. 3.24):
,
или
,
(3.33)
,
или
и т.д.
Таким образом, скорость любой точки плоской фигуры численно равна произведению угловой скорости фигуры на длину отрезка, соединяющего точку с МЦС, и направлена перпендикулярно этому отрезку в сторону вращения фигуры.
Из уравнений (3.33) следует, что
,
(3.34)
.
(3.35)
В реальных механизмах при произвольных положе-ниях звеньев определение расстояний до МЦС приводит к громоздким вычислениям. Поэтому в практических расчетах эти расстояния определяют графически по чертежу механизма, выполненному в масштабе.
МЦС очевидно, может лежать вне плоской фигуры. Однако в этом случае считается, что он принадлежит фигуре, так как с последней мы мысленно связываем нематериальную плоскость и считаем размеры фигуры неограниченными.
Таким образом:
для определения МЦС надо знать только направ-ление скоростей каких-нибудь 2-х точек А и В сечения тела (или траекторию этих точек), так как МЦС находится в точке пересечения перпендику-ляров, восстановленных в точках А и В к скорос-тям в этих точках (или касательным к траектории);
для определения скорости какой-нибудь точки тела надо знать модуль и направление скорости одной точки А тела и направление скорости другой точки;
угловая скорость тела как видно из (3.34) равна в каждый момент времени отношению скорости какой-нибудь точки сечения S к ее расстоянию до МЦС (точка P).
Рассмотрим частные случаи определения положе-ния МЦС.
Заданы скорость какой-либо фигуры и ее угловая скорость. Данный случай рассматривался при доказате-льстве существования МЦС. Кратко повторим рассужде-ния. Проведем из точки А (рис. 3.24) луч, перпендикуляр-ный к заданному вектору скорости в направлении, соответствующем направлению вращения, и отложим на этом луче отрезок
.
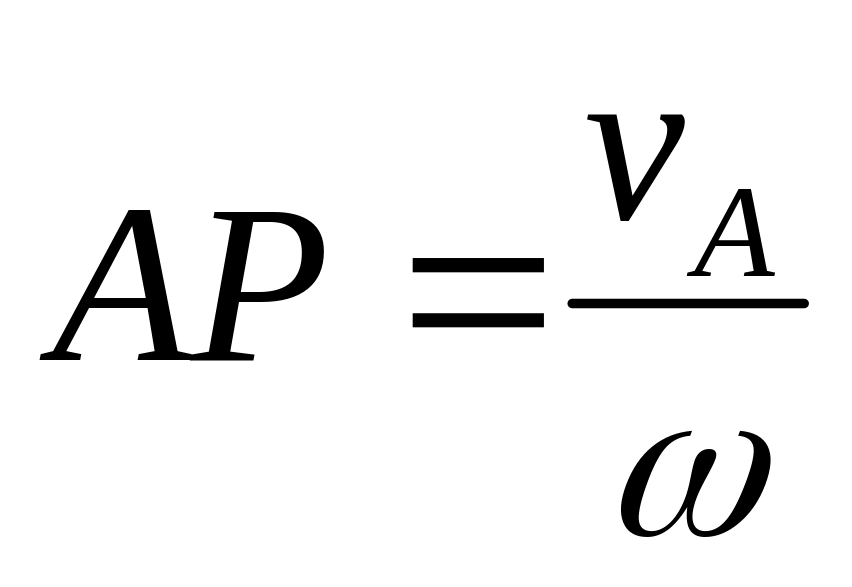Полученная точка Р и будет МЦС.Заданы направления скоростей двух точек плоской фигуры, скажем точек А и В, причем скорость точки А не параллельна скорости точки В. Поэтому точка пересече-ния перпендикуляров к скоростям точек А и В и будет являться МЦС (рис. 3.24).
Заданы скорости двух точек и плоской фигу-ры, причем они параллельны между собой и перпендику-лярны отрезку АВ (рис. 3.25). Проведем прямую линию через концы векторов скоростей. Тогда точка Р пересече-ния этой прямой с прямой АВ и будет МЦС.
Если скорости точек А и В равны между собой и перпендикулярны АВ (рис. 3.26, а), то МЦС находится в бесконечности. В данный момент угловая скорость фигу-ры равна нулю (
).
Следовательно, тело совершает мгновенно
поступательное движение и скорости
всех его точек в данный момент равны
между собой.
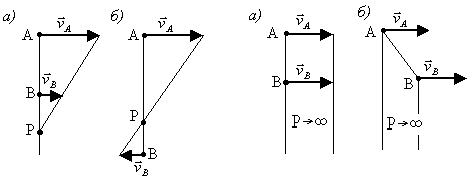
Рис. 3.25 Рис. 3.26
Заданы только направления скоростей двух точек А и В плоской фигуры. Причем они параллельны друг дру-гу, но не перпендикулярны отрезку АВ (рис. 3.26, б) Про-ведя перпендикуляры к заданным направлениям скорос-тей в точках А и В, находим, что мгновенный центр ско-ростей лежит в бесконечности. Следовательно, угловая скорость фигуры равна нулю ( ) , а тело совершает мгновенно поступательное движение. Таким образом, скорости всех его точек в данный момент времени равны между собой.
Термин «мгновенно поступательное движение» яв-ляется условным, так как в общем случае движения плоской фигуры равенство скоростей ее точек в фиксиро-ванный момент времени не означает равенства ускоре-ний этих точек, а равенство нулю угловой скорости фи-гуры не означает равенства нулю ее углового ускорения.
Е
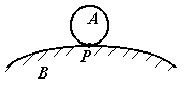сли
тело А катится без скольжения по
неподвиж-ному основанию В (рис.
3.27), то точки их контакта имеют одинаковые
скорости. А поскольку основание В
неподвижно, то скорость точки
=0,
тогда скорость точки кон-такта тела А
также имеет скорость
=0.
То есть точка контакта тела
А с неподвижной плоскостью
Рис. 3.27 является МЦС.
Пример. Колесо радиусом R катится без скольжения по прямому рельсу. Скорость центра колеса в рассматриваемый момент времени vС = 4 м/сек. Определить скорости точек О, А, В и D колеса, расположенных на концах взаимно перпендикулярных диаметров (рис. 3.28, а).
Решение. 1-й вариант. Примем за полюс центр колеса С (рис. 3.28, б). Тогда скорость любой точки колеса будет равна геометрической сумме скоростей полюса и скорости вращения этой точки вокруг полюса (3.30). Так как колесо катится без скольжения, то скорость точки О касания колеса с рельсом равна нулю vO = 0.
Точка О
является мгновенным центром скоростей.
В этой точке скорость вращения вокруг
полюса
и скорость по-люса
равны по модулю и противоположны по
направле-нию, то есть
=
-
.
Расстояния от точек О, А, В и D до полюса С равны. Следовательно, и вращательные скорости точек вокруг полюса тоже равны, то есть
=
=
=
=
.
Откладывая в каждой точке скорость полюса и враща-тельную скорость, перпендикулярную соответствующему ра-диусу колеса, находим:
м/сек,
м/сек,
м/сек.
Рис. 3.28
2-й вариант. Примем мгновенный центр скоростей колеса Р за полюс. Тогда скорости всех точек колеса определятся как вращательные скорости вокруг мгновенного центра скоростей. Модули скоростей всех точек найдутся по свойству пропор-циональности скоростей их расстояниям от мгновенного центра скоростей
м/сек.
Так
как
,
то
66
м/сек,
м/сек.
Найденные скорости точек направлены перпендикулярно соответствующим отрезкам в сторону вращения колеса (рис. 3.28, в). Аналогичное распределение скоростей имеет место при качении колеса без скольжения по любой поверхности.
3-й вариант. Графическое решение представлено на рис.3.28, г. Где, используя свойства плана скоростей, построен план скоростей, с помощью которого легко определяются скорости указанных точек.