3.3. Теорема об изменении

КОЛИЧЕСТВА ДВИЖЕНИЯ

Производная по времени от количества движения системы материальных точек равна главному вектору внешних сил действующих на систему

,

или в дифференциальной форме: Дифференциал количества движения системы материальных точек равен векторной сумме элементарных импульсов действующих на систему внешних сил

.

Решение задач с помощью теоремы об изменении ко­личества движения по сравнению с решением задач с ис­пользованием дифференциальных уравнений движения системы упрощается, поскольку применение теоремы ис­ключает необходимость рассмотрения внутренних сил си­стемы. Решение оказывается особенно простым в том случае, когда выполняется закон сохранения количе­ства движения.

Решение задачи с помощью теоремы об изменении ко­личества движения рекомендуется проводить в следую­щей последовательности.

1. Изобразить систему в положении, которое она зани­мает в промежуточный момент времени (t > 0).

2. Изобразить на рисунке все приложенные к системе внешние силы (как активные, так и реакции связей).

3. Провести оси координат. Если на систему действу­ют только параллельные силы, то одна из осей проводит­ся перпендикулярно направлению действия сил, в противном же случае оси проводятся наиболее естественным способом, вытекающим из условия задачи. Начало коор­динат следует совместить с положением основного тела при t = 0 или с положением его статического равновесия.

4. Составить уравнения теоремы об изменении коли­чества движения в проекциях на выбранные, оси коорди­нат в дифференциальной форме:

dQ_х/dt = , dQ_y/dt= , dQ_z/dt = ,

или в интегральной форме:

, , .

3. Изобразить на рисунке абсолютные и относитель­ные скорости тел системы и подсчитать проекции коли­чества движения системы на оси координат. Необходимо иметь в виду, что в выражения

, ,

входят абсолютные скорости. Если направление скорости какой-либо точки заранее не­известно, то скорость направляют в сторону положитель­ных направлений осей координат.

6. Подставив выражения проекций количества движе­ния системы в формулы теоремы (п. 4), определить не­известные силы пли получить дифференциальные уравнения движения интересующей нас части системы.

7. Проинтегрировать полученные дифференциальные уравнения и найти искомые неизвестные.

8. Если выполняется закон сохранения количества движения или какой-либо его проекции (т. е. если = 0 или = 0 и, следовательно, = const = или

Q_x= const = Q_x0), то задача сводится к определению количеств движения системы (или их проекции) в на­чальный и заданный (или текущий) моменты времени и приравниванию их друг другу

Пример 1. На железнодорожной платформе, свободно стоя­щей на рельсах, установлена лебедка А с барабаном радиусом r (рис. 400). Лебедка предназначена для перемещения по платформе гру­за B массой т₁. Масса платформы с лебедкой m₂. При включении ле­бедки барабан вращается по закону, ω = f(t) рад/с. В начальный момент система неподвижна. Пренебрегая трением, найти закон изменения скорости платформы после включе­ния лебедки.

Р ешение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести , и реакции , ) будут вертикальными. Проведем ось х перпендикулярно им и за­пишем теорему об изменении количества движения системы в про­екциях на эту ось:

.

Таким образом, мы имеем

Риc. 400 случай сохранения проекции

количества движения системы: Q_x= const = Q_x0, поскольку в начальный момент система неподвижна, Q_x0 = 0, и решение задачи сводится к тому, чтобы найти количество движе­нии в момент времени t > 0 и приравнять полученное выраже­ние нулю. Обозначим скорость тележки через и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим ; при этом v₂ = ωr. Абсо­лютная скорость груза равна v_B = v₁+ v₂ = v₁ + ωr. Тогда

Q_x = m₂ v₁+ (т₁v₁ – ωr) = 0,

откуда

.

Знак минус показывает, что платформа будет перемещаться в сто­рону, противоположную относительному движению груза.

Пример 2. Электрический мотор массой т₁ установлен без креплений на гладком горизонтальном фундаменте (рис. 401). На валу мотора под прямым углом за­креплен одним концом невесомый стержень длиной l, на другой конец стержня насажен точечный груз А массой m₂. В момент включения мо­тора стержень занимает вертикаль­ное положение. После включения мотора угловая скорость его вала по­стоянна и равна ω. найти:

1 ) горизонтальное движение мотора; 2) силу давления мотора на фундамент.

Решение. Изобразим мотор в положении φ = ωt > 0. К системе приложены внешние силы: силы тяжести , и реакция фундамента . Все они

Рис. 401 вертикальны, поэтому ось х проведем гори­зонтально. Начало отсчета выберем в положении, которое занимает центр мотора при φ = 0, т. е. при t = 0. Запишем теорему в про­екциях на оси координат:

dQ_х/dt= ,

следовательно, Q_х = const = Q_х0 = 0, так как до включения мотор и груз А были неподвижны; dQ_у/dt = = = N - Р - Q, откуда N = g (m₁+ m₂) + dQ_y/dt. Таким образом, задача сводится к определению проекций количества движения системы. Пусть центр мотора дви­жется вправо со скоростью v_c, тогда

Q_x = m₁v_c + m₂v_Ax, Q_у = m₂v_Ay,,

где — абсолютная скорость груза А. Переносной скоростью гру­за является скорость мотора , относительной — скорость при вращении груза А вокруг точки С: v_r = ωl. Тогда v_Ax= v_с – ωl cos ωt, v_Aу =-ωl sin ωt и, следовательно,

Q_x= (m₁ + m₂) v_c - m₂ωl cos ωt, Q_y = - m₂ ωl sinωt.

Так как Q_х = 0, получаем, что

откуда + С. Из начальных условий (t = 0, х_С = 0) находим С = 0 и окончательно

,

т. е. центр мотора будет совершать горизонтальные гармонические колебания относительно своего начального положения с амплиту­дой m₁l/(m₁ + т₂). Сила давления мотора на фундамент по вели­чине равна реакции фундамента, действующей на мотор, поэтому

N = g (т₁+ m₂) + = g(т₁+ т₂) - m₂ω²l cos ωt).

Минимальное значение реакции достигается при cos ωt = 1, т. е. при φ = 0, а максимальное — при φ = π:

N_min = g(m₁ — m₂) + т₂ω²l, N_max = g(m₁+ m₂) + m₂ω²l.

Если N_min < 0, то мотор начинает подпрыгивать на фундаменте. В этом случае его угловая скорость

.

Пример 3. Призма А мас­сой т₁ лежит на гладкой наклон-ной плоскости. По ней дви­жется тело В массой т₂ при­чем это относительное движе­ние происходит по закону s = nt²/2. В начальный момент тело А находится в покое. Оп­ределить зависимость скорости тела А от времени (рис. 402).

Решение. Система состоит из двух тел: А и В. На нее действуют следующие внешние силы: - сила тяжести тела А, - сила тяжести тела В, - реакция наклонной плоскости. Для решения задачи применим теорему об изме­нении количества движения системы в интегральной форме в про­екциях на ось х:

,

г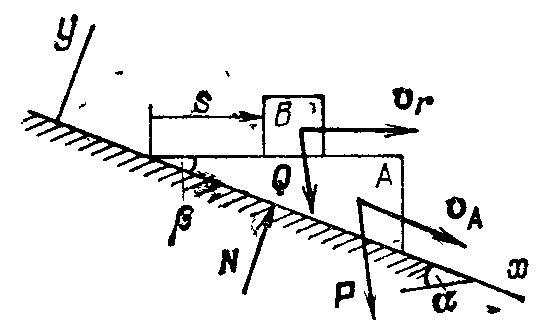 де Q_0x — проекция количества движения системы в начальный момент времени, а Q_x — та же проекция в произвольный момент времени t.

Определим количество движения системы в момент t: , где -количество движения тела А, —количество движения тела В, и — абсолютные скорости тел А и В.

Для тела В переносной

Рис.402 скоростью является скорость тела А ( ), а относительная скорость nt, следовательно,

.

Проекция количества движения системы на ось х равна

Q_x = (m₁+ m₂)v_A + m₂nt cos β.

По условию при t = 0, v_a = 0, и поэтому Q_х0 = 0. Определим про­екции импульсов внешних сил на ось х за время t:

,

,

, так как N_x= 0.

Подставив найденные величины в формулу теоремы, получим

(m₁ + m₂)v_А + т₂пt cos β = g(m₁+ m₂)t sin α ,

или

.

Таким образом, скорость призмы А пропорциональна времени, а ее направление зависит от знака выражения, стоящего в скобках. Призма будет двигаться вверх по наклонной плоскости, если g sin α – т₂п cos β/(m₁ + m₂) < 0, т. е. если относительное ускоре­ние а_r = = п тела В превышает значение

.