Вопросы

1. Интуитивные определения понятия алгоритма, их недостатки.

2. Определения алгоритма по Колмогорову, по Маркову. Сравнение этих определений.

3. Общие требования к алгоритму, не зависящие от используемого определения алгоритма.

4. В чем заключается требование конечности записи алгоритма?

5. В чем заключается требование конечности действий алгоритма?

6. В чем заключаются требования универсальности и правильности алгоритма?

7. Постройте алгоритм получения положительной оценки на экзамене.

8. Постройте алгоритм для процесса завязывания шнурков, проверте его работу на своем коллеге.

9. Для чего служит машина Тьюринга?

10. Что представляет из себя алгоритмически неразрешимая проблема?

11. Является ли алгоритмически неразрешимой проблема решения уравнения: 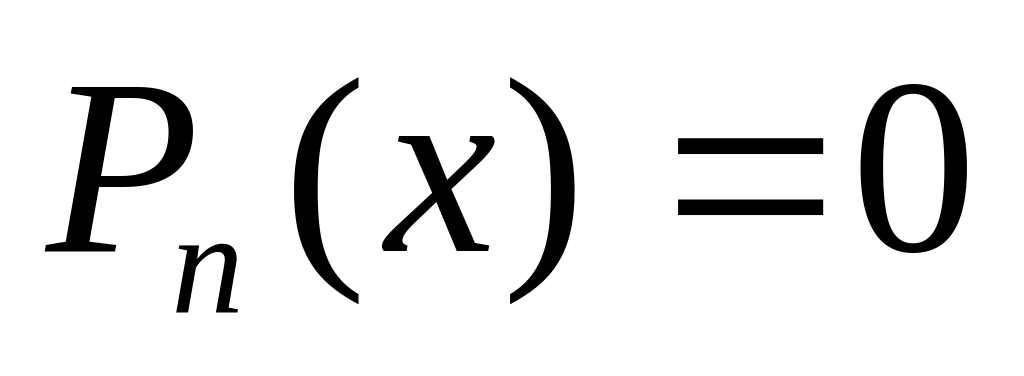, где – многочлен степени n? Почему?

Література

1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с.

2. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с.

Лекция 2. Численные алгоритмы и их характеристики.

План

1. Особенности численного результата задачи

2. Теория возмущений и числа обусловленности задачи

3. Влияние ошибок округления на алгоритмы

4. Программирование численных алгоритмов

1. Особенности численного результата задачи

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами. Численные алгоритмы занимают очень существенное место среди всевозможных алгоритмов, включающих, например, логические - алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям, например, алгоритм поиска пути на графе.

При решении произвольной реальной задачи в общем случае невозможно получить точное значение искомого численного результата [53,55,60]. Существование неустранимой погрешности в математической модели объекта или процесса, фигурирующего в задаче (математическое описание задачи является неточным), погрешности входных данных, многие из которых в реальных условиях получены экспериментально, погрешность численного алгоритма, используемого для решения, и вычислительная, погрешности, возникающие при каких-либо дополнительных воздействиях на объект, которые часто трактуются как возмущения входных данных, приводят к необходимости их совокупного учета при оценке погрешности результата. Даже в случае, когда входные данные математической модели не имеют погрешностей, а алгоритм, выбранный для решения полученной математической задачи является точным [54], избежать вычислительной погрешности при проведении вычислений в системе чисел с плавающей точкой, а значит и погрешности в полученном результате, невозможно [69]. После построения математической модели реального процесса, которая необходимо удовлетворяет требованию адекватности (решение математической задачи, полученное с ее помощью, незначительно отличается от истинного решения реальной задачи), исходная задача и ее математическая формализация в процессе решения и анализа полученного результата, как правило, не разделяются. Однако, в силу особенностей машинной арифметики, невозможно в общем случае получить точное решение даже смоделированной математической задачи (пренебрегая неустранимой погрешностью и погрешностью метода) [53,60]. Действительно, для конечной системы чисел с плавающей точкой , реализованной в ЭВМ для представления бесконечного множества вещественных чисел , арифметические операции обладают своими особенностями: основные законы арифметики могут нарушаться. Рассмотрим это подробнее.

Множество чисел с плавающей точкой характеризуется четырьмя параметрами: числом разрядов , основанием системы счисления , границами изменения показателя степени , при том, что каждое число представляется в виде:

, (200)

где - целые числа, такие, что , а .

Часть в (200) – дробная часть, или мантисса числа . Система нормализованная, если для выполняется: .

Таким образом, очевидно, что точно в системе могут быть представлены лишь конечное множество действительных чисел. Если число находится в границах представления чисел данной системы , однако не совпадает ни с одним из них, то оно приближается одним из чисел за счет операции округления (усечения) [Бахвалов], получая в результате определенную погрешность.

Пусть . Результат выполнения арифметических операций над в системе будем обозначать , где символ «*» может быть конкретизирован операцией сложения, вычитания, умножения, деления.

Идеальным для выполнения арифметических операций в системе является ситуация, когда сама операция над числами выполняется точно, а затем результат, при необходимости, либо усекается, либо округляется. На практике при выполнении арифметических операций обычно выделяются дополнительные разряды, полученный результат нормализуется, и лишь затем выполняется округление (усечение).

Рассмотрим гипотетическую систему , для которой , , и вычислим в этой системе сумму 0.12+0.17+0.87. В точной арифметике 0.12+(0.17+0.87)=(0.12+0.17)+0.87. В системе результат левой части равен:

при этом результат правой части:

Очевидно, результат даже такого простого выражения зависит от порядка выполнения операций. Таким образом, одному алгоритму, записанному «на бумаге», соответствует множество «машинных» алгоритмов, в каждом из которых свой порядок выполнения действий, а значит, может быть и другой результат.

Полученное приближенное (в силу перечисленных выше причин) решение некоторой вычислительной задачи может рассматриваться как точное решение, но другой, возмущенной задачи ( отличается от возмущением входных данных) [60]. В этом случае для определения качества полученного приближения необходимо иметь возможность оценить степень зависимости решения от возмущений исходных данных.