2.1.5. Прискорення руху точки
Прискорення – це фізична величина, що характеризує зміну вектора швидкості руху точки за часом.
На підставі цього означення і змісту підрозділу 2.1.3 можна визначити величину і напрям прискорення точки:
.
(2.23)
Вектор
напрямлений по дотичній до годографа
вектора швидкості
.
Знайдемо прискорення точки трьома способами опису її руху.
Якщо рух точки задано векторним рівнянням
,
то
швидкість
,
і на підставі (2.23) прискорення
.
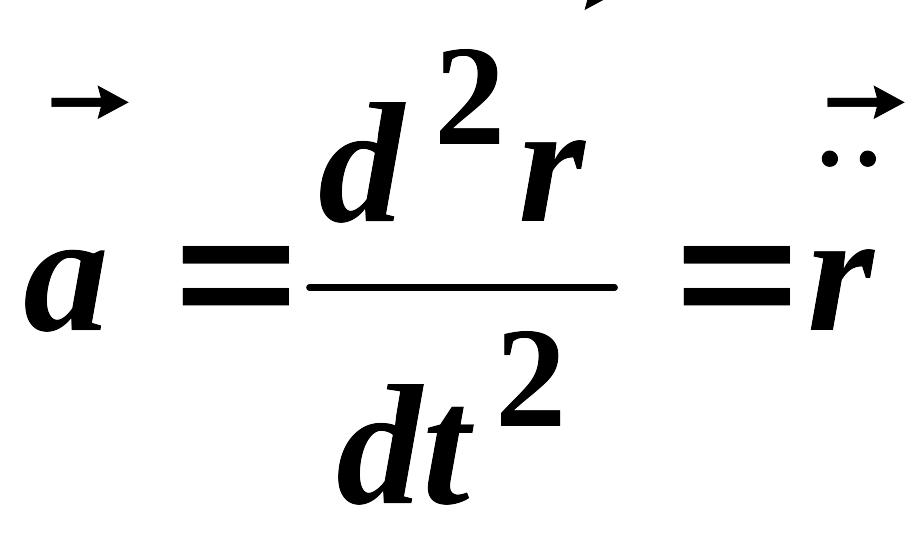(2.24)
Для визначення прискорення точки координатним способом скористаємося рівностями (2.7) і (2.24):
.
Розкладаючи вектор прискорення по ортах декартової системи координат
і порівнюючи вирази, маємо
.
(2.25)
Модуль вектора і його напрямні косинуси знаходимо за відомими формулами аналітичної геометрії:
;
(2.26)
.(2.27)
Формули (2.25)-(2.27) визначають вектор прискорення координатним способом.
Знайдемо прискорення точки, користуючись натуральним способом. Із (2.22) і (2.23) дістанемо
.
(2.28)
Зауважимо,
що орт
змінює свій напрям зі зміною дугової
координати
,
тобто його можна розглядати як складну
функцію часу
.
Отже,
.
(2.29)
Розглянемо похідну від за :
.
Знайдемо
напрям вектора
і його модуль.
Вектор
напрямлений, як відомо, по дотичній до
годографа вектора
.
Оскільки
– одиничний вектор, його годографом є
крива, розміщена на поверхні сфери
одиничного радіуса. Тому вектор
утворює з вектором
прямий кут (рис. 2.8). З’ясуємо, вздовж
якої нормалі напрямлений вектор
.
Для цього розглянемо граничний напрям
вектора
.
Щоб його побудувати, проведемо одиничні
вектори
і
в сусідніх точках М
і
,
де
.
Побудуємо в точці М
вектор
,
що дорівнює
.
Тоді
.
Якщо
,
точка
,
то площина трикутника
,
обертаючись навколо вектора
,
наближається до певного граничного
положення. Це граничне положення площини
трикутника
знаходиться в стичній площині кривої
в точці М.
Отже, нормаль, вздовж якої напрямлений
вектор
,
лежить в стичній
площині. Цю нормаль називають головною
нормаллю
кривої.
Зауважимо, що всі точки будь-якої плоскої кривої лежать у стичній площині.
З рис. 2.8 видно, що вектор напрямлений у бік угнутості кривої, тобто в бік її центра кривини.
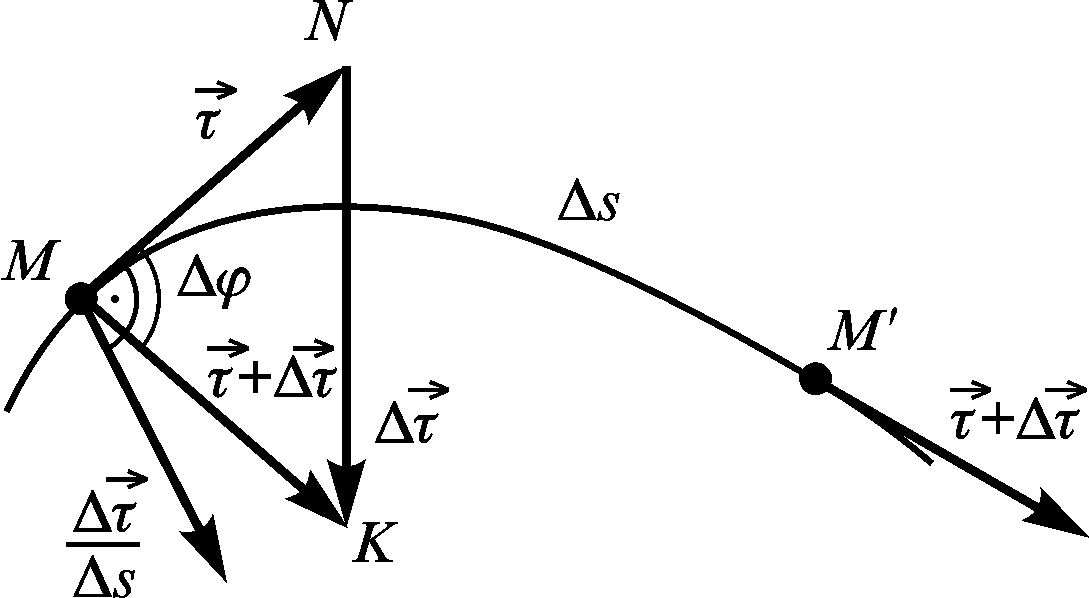
Рисунок 2.8
Визначимо модуль вектора
.
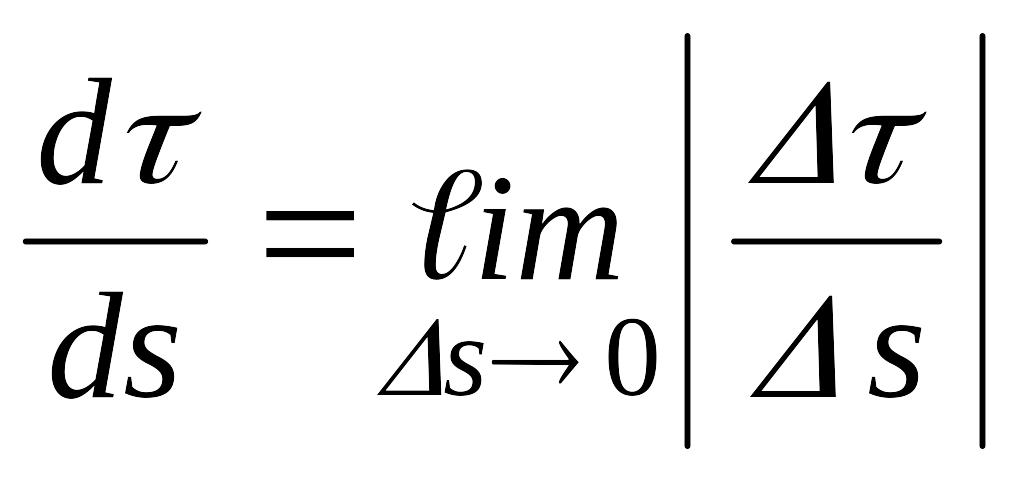З
трикутника MNK
(рис. 2.8) знаходимо
,
оскільки
,
тому
.
Оскільки
,
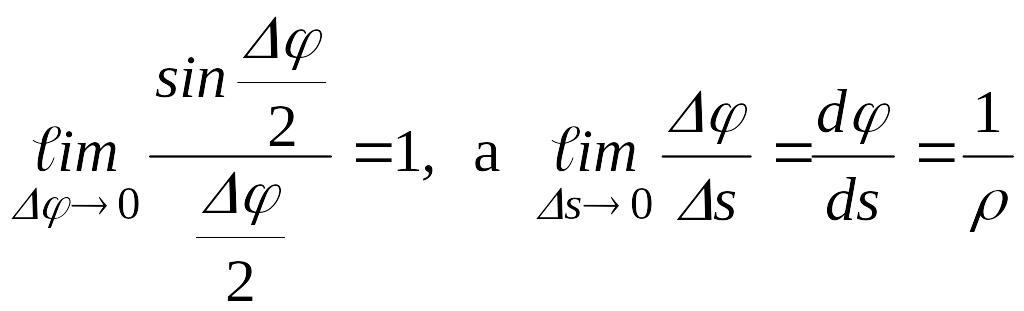де
– радіус кривини кривої, то
.
(2.30)
Позначимо
орт головної нормалі через
і напрямимо його в бік угнутості кривої.
Тоді
.
(2.31)
Побудуємо
місцевий координатний базис – натуральний
тріедр (рис. 2.9). Орти дотичної і головної
нормалі створюють стичну площину кривої.
Проведемо нормаль до цієї площини. Цю
нормаль називають бінормаллю,
її орт
.
У площині (
)
розміщені всі нормалі до кривої, тому
орти (
)
утворюють нормальну
площину кривої. Орти (
)
утворюють спрямну
площину кривої.
Повернемось до визначення прискорення точки. На підставі (2.29) і (2.31) вираз (2.28) набуває вигляду
.
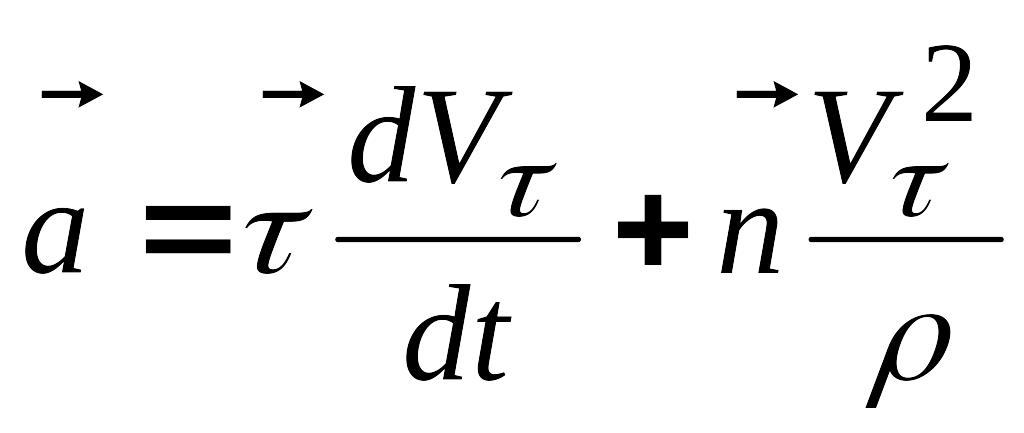(2.32)
Зауважимо,
що
,
де
– модуль швидкості.
Розкладемо вектор по ортах натурального тріедра:
(2.33)
і порівняємо отриманий вираз із формулою (2.32):
.
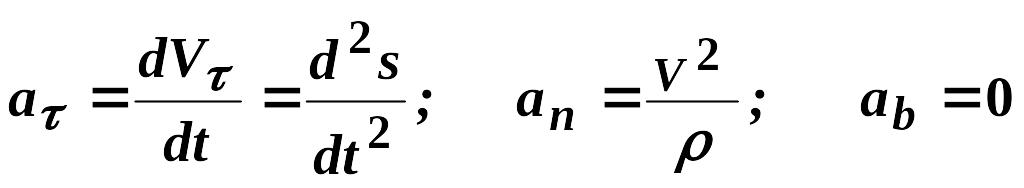(2.34)
Як видно з (2.33), (2.34), проекція вектора прискорення на бінормаль дорівнює нулеві.
Отже,
вектор прискорення точки лежить завжди
у стичній площині траєкторії точки.
Проекцію
називають дотичним, або тангенціальним
прискоренням, проекцію
–
доцентровим або нормальним прискоренням.
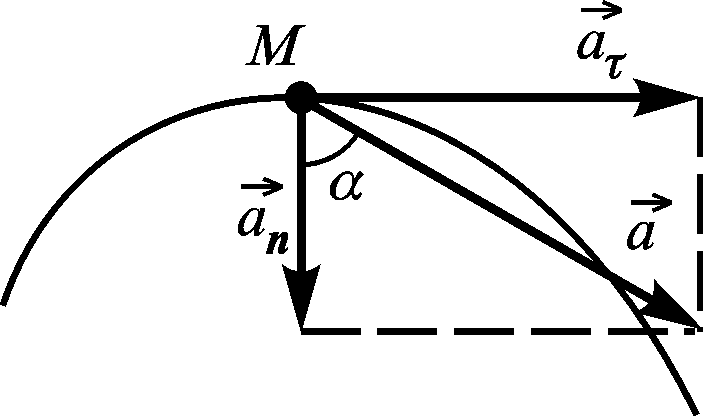
Повне прискорення точки є векторною сумою дотичного і нормального прискорень (рис. 2.10).
.
|
|
Рисунок 2.9 |
Рисунок 2.10 |
Модуль прискорення і його напрям:
.
(2.35)
Отже, формули (2.33), (2.34), (2.35) визначають вектор прискорення натуральним способом.