РОЗДІЛ 2

КІНЕМАТИКА

2.1. Кінематика матеріальної точки

2.1.1. Основні положення

Кінематика – це розділ класичної механіки, в якому вивчають геометричні властивості механічних рухів незалежно від фізичних факторів, що спричиняють ці рухи, тобто незалежно від сил.

Кінематика безпосередньо спирається на основні положення геометрії. До цих положень приєднується поняття про час. Кінематику називають також “геометрією рухів”.

Рух тіл кінематика вивчає відносно певних систем координат. Ці системи координат вважатимемо рухомими або умовно нерухомими залежно від конкретних умов механічної задачі. Системи координат називають також системами відліку.

Основне завдання кінематики – вивчення законів руху матеріальних об’єктів (точок, систем точок, твердих тіл).

Закон руху точки або тіла визначається зв’язком між довільним положенням точки чи тіла в просторі з часом.

Кінематику поділено на кінематику точки і кінематику абсолютно твердого тіла.

Законом руху матеріальної точки називають спосіб її переходу з одного довільного положення у просторі й часі в інше довільне положення.

2.1.2. Способи визначення руху точки

Рух точки в просторі визначається трьома основними способами: векторним, координатним і натуральним.

Векторний спосіб найчастіше застосовують в різних теоретичних дослідженнях. Виберемо в просторі умовно нерухому точку О, відносно якої маємо дослідити рух точки М (рис. 2.1). Проведемо з точки О в точку М радіус-вектор . Криву, по якій рухається точка, називають її траєкторією. Зі зміною положення точки М на траєкторії відповідно змінюється вектор . Кожному моменту часу відповідає певне значення радіуса-вектора , тобто є функцією часу:

Рисунок 2.1

. (2.1)

Рівняння (2.1) визначає положення точки в просторі в довільний момент часу. Отже, воно визначає закон руху точки і називається векторним рівнянням руху точки. З геометричної точки зору рівняння (2.1) можна розглядати як рівняння траєкторії точки.

Розглянемо координатний спосіб. Визначимо поло-ження точки, застосовуючи ортогональну нерухому систему декартових координат (рис. 2.2). Координати точки однозначно визначають її положення. Кожному моменту часу відповідає сукупність координат точки М. Отже, координати точки є функціями часу

(2.2)

Рисунок 2.2

Функціональні залежності (2.2) називають кінематичними рівняннями руху точки. Вони дають змогу визначити положення точки в просторі в довільний момент часу, тобто є законом руху точки.

З аналітичної геометрії відомо, що (2.2) – це рівняння кривої, вздовж якої рухається точка, тобто рівняння траєкторії точки в параметричній формі. Щоб знайти рівняння траєкторії точки в координатній формі, досить з цих рівнянь вилучити параметр . Наприклад, розв’язуючи останнє рівняння системи (2.2) відносно і підставляючи це співвідношення в перші два рівняння, дістанемо

(2.3)

Два останні рівняння (2.3) визначають траєкторію точки як лінію перетину двох циліндричних поверхонь, що проектують траєкторію на координатні площини і .

Крім декартової, користуються й іншими системами координат: на площині – полярною системою координат ( ); у просторі – циліндричною ( ) або сферичною ( ) та іншими криволінійними системами координат. Закон руху точки в цих системах координат визначається аналогічно. Наприклад, у полярній системі координат рівняння руху точки мають вигляд

. (2.4)

Легко встановити зв’язок між векторним і координатним способами визначення руху точки. Проведемо з початку координат у точку М радіус-вектор і розкладемо його по ортах осей координат:

. (2.5)

Як відомо, координати точки М дорівнюють проекціям радіуса-вектора на координатні осі (рис. 2.2). Отже,

. (2.6)

Підставивши (2.6) в (2.5), дістанемо

. (2.7)

Залежність (2.7) установлює зв’язок між векторним і координатним способами визначення руху точки.

К

Рисунок 2.3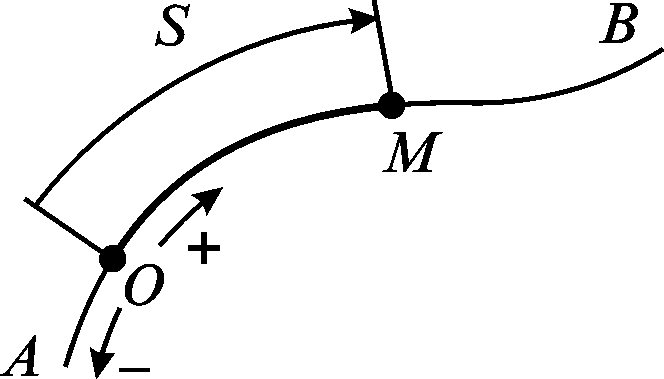

оординатний спосіб визначення руху точки в просторі застосовують як у теоретичних дослідженнях, так і при розв’язуванні конкретних задач.

Натуральним способом визначення руху точки користувався ще Л.Ейлер [ 5 ]. Припустимо, що траєкторія АВ точки М відома (рис. 2.3). Виберемо фіксовану точку О на траєкторії як початкову. Умовимося вважати один напрям від початкової точки О вздовж траєкторії додатним, а протилежний – від’ємним. Положення точки на траєкторії визначимо довжиною дуги , тобто дуговою координатою точки. Кожному моменту часу відповідає певне положення точки на траєкторії, отже, і певне значення її дугової координати. Таким чином, дугова координата є функцією часу

. (2.8)

Рівняння (2.8) називають законом руху точки по траєкторії. Закон руху точки в просторі визначається сукупністю всіх даних: траєкторією точки, положенням початкової точки О, додатним і від’ємним напрямами відліку і рівнянням (2.8).

Натуральний спосіб визначення руху точки в просторі застосовують і в різних теоретичних дослідженнях, і при розв’язуванні конкретних задач. Особливо доцільно його застосовувати, коли відомі форма і положення в просторі траєкторії точки.

Розглянемо поняття про шлях, який проходить точка М. Зауважимо, що слід розрізняти дугову координату і шлях , що його проходить точка за проміжок часу . Щоб визначити шлях , розіб’ємо проміжок часу на проміжки ( ) так, щоб протягом кожного проміжку точка рухалася в одному напрямі. Нехай кожному проміжку часу відповідає приріст дугової координати . Шлях визначається так

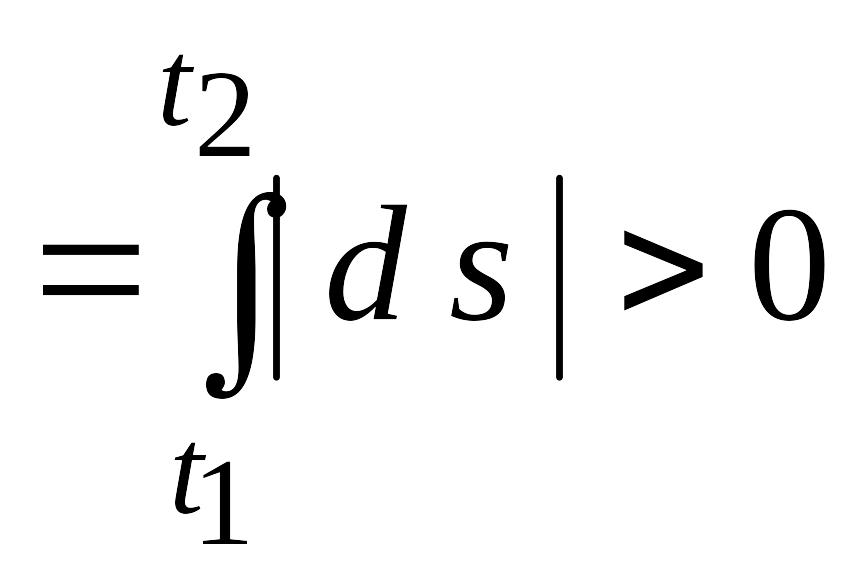. (2.9)

Зрозуміло, що шлях є монотонно зростаючою функцією часу.

Звичайно, між натуральним способом визначення руху точки і першими двома способами існує зв’язок. Не вдаючись до подробиць, зауважимо, що радіус-вектор точки при натуральному способі визначення руху точки можна розглядати як функцію дугової координати , тобто як складну функцію часу

(2.10)

. (2.11)

Зв’язок між натуральним і координатним способами визначення руху легко знайти, обчислюючи за відомими формулами диференціальної геометрії елемент дуги траєкторії:

. (2.12)

Вибір знака кореня відповідає вибору додатнього напряму відліку дугової координати при незмінному напрямі руху точки по траєкторії.