18. Закони алгебри висловлень.

Певні логічні операції зв’язані між собою законами. Ці закони називають законами алгебри висловлень:

1) закон подвійного заперечення висловлення: .

2) закон протиріччя: 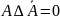. Цей закон пов’язує висловлення з його запереченням операцією кон’юнкції. Він означає, що два протилежні судження не можуть бути одночасно істинними.

3) закон виключеного третього: 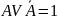. Цей закон пов’язує висловлення з його запереченням операцією диз’юнкції, і означає, що з двох протилежних тверджень завжди одне є істинним.

4) закони комутативності диз’юнкції та кон’юнкції:

.

5) закони асоціативності диз’юнкції та кон’юнкції:

;

.

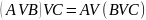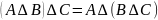6) дистрибутивні закони, які пов’язують кон’юнкцію та диз’юнкцію:

;

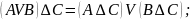
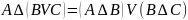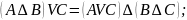
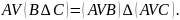
Закони, які стосуються операції заперечення диз’юнкції та кон’юнкції двох висловлень, були названі на честь шотландського математики де Моргана, який їх сформулював:

1)заперечення диз’юнкції двох висловлень дорівнює кон’юнкції заперечень цих висловлень:

2) заперечення кон’юнкції двох висловлень дорівнює диз’юнкції заперечень цих висловлень:

19. Означення предиката. Область визначення і область істинності.

Предикат – це речення у простому висловленні, які вміщують змінні, і для яких не можна визначити логічну вартість, бо при підстановці замість змінних певних значень вони перетворюються то в істинні, то в хибні висловлення. Предикати можуть бути одномісними, двомісними чи тримісними залежно від кількості змінних. Одномісним предикатом називають речення А(х) із змінною х, яке задане на певній множині Х і при підстановці значень змінної перетворюється в істинне чи хибне судження. Областю визначення предиката А(х) називають множину тих значень змінної х, при яких предикат перетворюється в істинне чи хибне судження. Область істинності предиката А(х) – це множина тих значень змінної, при яких цей предикат перетворюється в істинне судження. Область істинності предиката позначають символічно:

.

20. Дії над предикатами.

Над предикатами виконуються ті ж дії, що й над висловленнями, однак обов’язковою умовою є одна і таж область визначення для предикатів:

1) заперечення предиката А(х), заданого на множині Х – це такий новий предикат 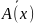, який перетворюється в істинне висловлення при тих значеннях змінної х з області визначення Х, при яких даний предикат А(х) перетворюється в хибне висловлення. Область істинності заперечення предиката, заданого на певній множині – це доповнення до області істинності даного предиката.

2) кон’юнкція двох предикатів А(х) та В(х), заданих на множині Х – це такий новий предикат 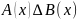, який перетворюється в істинне висловлення лише при тих значеннях х з області визначення Х, при яких обидва ці предикати одночасно перетворюються в істинні судження. Область істинності кон’юнкції предикатів – це переріз областей істинності цих предикатів.

3) диз’юнкція двох предикатів А(х) і В(х), заданих на множині Х – це такий новий предикат 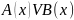, який перетворюється в істинне висловлення лише при тих значеннях х з області визначення Х, при яких хоча б один з предикатів перетворюється в істинне висловлення. Область визначення диз’юнкції двох предикатів – це об’єднання областей істинності даних предикатів.

4) Імплікація двох предикатів А(х) і В(х), заданих на множині Х – це новий предикат 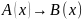, який перетворюється в хибне висловлення при тих значення х з області визначення Х, при яких предикат А(х) перетворюється в істинне висловлення, а предикат В(х) – в хибне. Область істинності імплікації – це об’єднання доповнень до області істинності предиката А(х) з областю істинності предиката В(х).

5) Еквіваленція двох предикатів А(х) і В(х), заданих на множині Х – це новий предикат 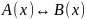, який перетворюється в істинне висловлення при тих значеннях змінної х з області визначення Х, при яких обидва предикати перетворюються у висловлення однакової логічної вартості (або одночасно істинні, або одночасно хибні). Область істинності еквіваленції предикатів – це об’єднання перерізу областей істинності даних предикатів з перерізом доповнень до цих областей істинності.