Собственные числа и собственные вектора линейного пространства.

-инвар.следовательно= применим к этому вектору оператор.

Определение:

Если , тогда не нулевой векторназывается собственным вектором оператораА, отвечающего собственного числа.

Примеры:

1. Проектир.

всякий вектор из ядра

a)вектор собственный с собственным числом 0.

b)- тоже собственный вектор с собственным числом 1.

2) тогда инвариантное подпространство.

Рассмотрим вектор

тогда

собственный вектор с собственным числом 2.

3) A– поворот плоскостивокруг координат напет. с вит.

4))

Характеристический многочлен линейного оператора.

Теорема:и пусть в нем зафиксирован базис, тогда- собственное число оператораA, тогдаудовлетворяет выражению

- единичная матрица,- корень.

Замечание:многочлен-характеристический многочлен оператораА.

Доказательство:

- собственное число воспользуется изоморфизмом – зафиксируем базис.

- базис- матрица.

- собственное число, то есть, такой, чтоперейдем к равенству координатных столбцов

- матричное равенство, следовательно, система имеет решение не равное 0.

по правилу однородно СЛУ.

2. пусть докажем, что- собственное число.

корень уравнения

Рассмотрим СЛУ. так какпоскольку есть взаимно однозначное соответствие, то есть и вектор.

x-собственный вектор,собственное число.

Теорема Независимость характеристического многочлена от выбора базиса.

- не зависит от базиса.

Доказательство:

Рассмотрим 2 базиса

- базисы,- матрица перехода.

сравним

ч.т.д.

Для вычисления собственных чисел и собственных векторов используется матрица оператора, но сами собственные числа не зависят от выбора базиса.

e₁,..,e₂ |

}Базисы,- матрица перехода

f₁,..,f₂ |

сравним

и т.д.

Для вычисления собственных чисел и собственных секторов используется матрица оператора, но сами собственные числа не зависят от выбора базиса.

50 Условия диагонализации линейного оператора

Оператор диагонализации называется оператором если существует базис в котором матрица этого оператора диагональная.

Теорема: ОператорA:L  L – он диагонализуем тогда и только тогда, когда существует базис вL, состоящий из собственных векторов оператора ; (сущe₁,..,e_n - ,базис)

Доказательство:

1. пусть А – диаганализуема тогда сущ базис e1,..,en

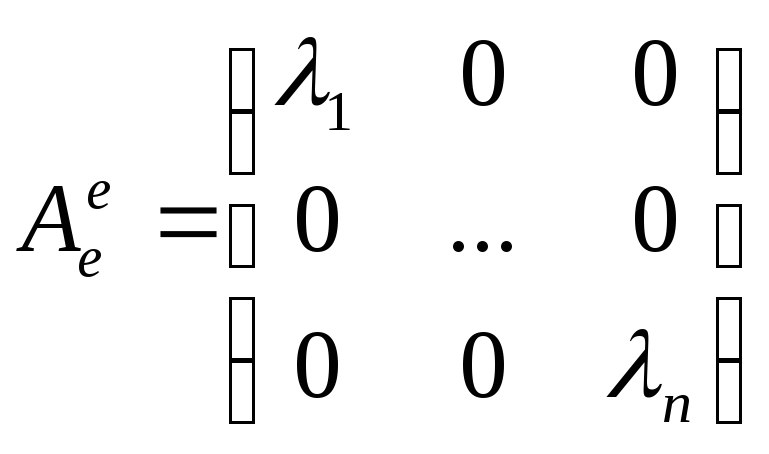
e1 его образ[A_е1] и рассмотрим под диагональный столбец в базисе е

т.е. т.е. этот вектор собственный так же и остальные вектора.

пусть есть базис сущ e1,..,en – собственные вектора , 1<=i<=n 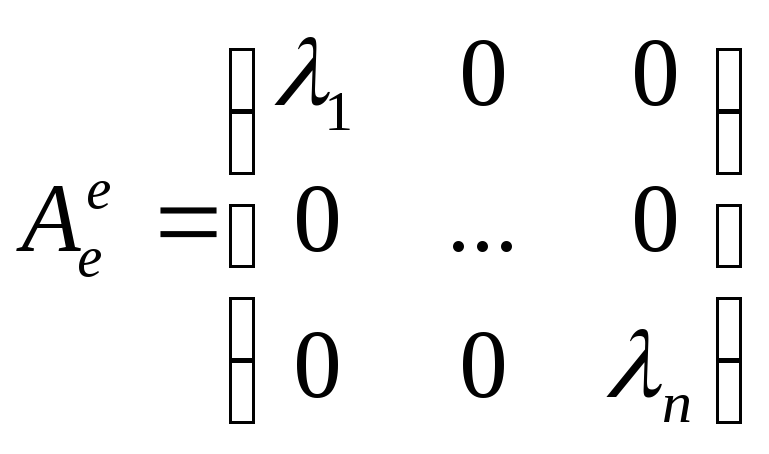т.е. оператор диаганализуем и т.д.

Когда есть базис из собственных векторов.

Теорема: линейно независимых собственных векторов

Пусть есть линейный оператор A:LLи пусть есть к – собственных чисел (различных)- с.ч.для всякихi<>j тогда отвечающие им собственные вектора лин зав(ЛНЗ)e1,…en – ЛНЗ Доказательство: (по индукции)

1. k=1 по определению собственный вектор не нулевой, а набор из одного вектора ЛНЗ e1<>0; e1 – ЛНЗ

2. e1,…,e_k-1 – ЛНЗ – предположение

Рассмотрим множество() А котороеe1,…,ek – ЛНЗ диаганал (1) применим линейный оператор

а) тогда получим

т.к. e1,…,e_k-1 – ЛНЗ следовательно все равны 0

т.к. тогда средиесли i<k

это означает что

тогда

тогда т.к.ek<>0 то

т.е. вектора ЛНЗ

б)

т.к. е1,…,е_к-1 – ЛНЗ

то т.к.то следовательно

т.к. все то следовательно() следовательно

т.е набор ЛНЗ

Следствие: Если лин оператор A:LL dimL=n n – различные собственные числа

существуют - собственные числа (все различные) тогда А – диаганализуем

Пример: A

x3=0 x1=-x2

x1-с.ч. x3=x2=0

x2=x3 x1=2*x2

e3=3*e3 e2=2*e2 e1=e1

2. 

rangM=1

размерность решений равна 1

rang (A-E)=1

собственный вектор (?????????????)

3. 

если мы рассматриваем под R т.е. det не имеет корней нет с.ч. и с.в.