Размерности подпространства, сумма и пересечения.

Пусть L– конечномерное пространство,M– подпространство, тогда размерностьdim M < dim L.

Доказательство

Пусть - это означает, что есть базисэлементов.

- базисMэто ЛНЗ из пространстваL.

Линейная оболочка: набор векторов , тогда его оболочка это множество всех конечных линейных комбинаций этого набора.

(- вектора принадлежащие линейному пространству (надo? )k

Доказать самим:

Линейная оболочка – это подпространство.

Рассмотрим линейную оболочку набора

значит - такой который лежит вLи такой, что- ЛНЗ

Рассмотрим линейную оболочку она может совпасть сLили может не совпасть – в этом случаепроцесс дополнения базиса оборвется за конечное число шагов, когда мы получим базис всего пространстваL.

При этом первый шаг будет нетривиальным поэтому, следовательно,ч.т.д.

Замечание:за одно мы показали, что любой линейно независимый набор в конечно мерном пространстве можно дополнить до базиса.

Теорема: пусть есть пространствоL–лин., и есть в нем два подпространства –

-M₁,M₂, тогда справедливо равенство.

Доказательство: Выберем специальным образом базис

Теперь специальным образом выберем базис

- , базис, а теперь дополним этот базис до базисаM₁и до базисаM₂

,- базис пространстваM₁­

- базис пространстваM₂

Рассмотрим набор векторов.

-это базис суммы

Докажем это. Для этого надо доказать, что набор ЛНЗ и это система образующих.

Докажем, что это система образующих:

Пусть -это означает, что вектор- переставлен в виде суммы двух.

, но тогдаa-можно записать как комбинацию:

таким образом этот набор система образующих.

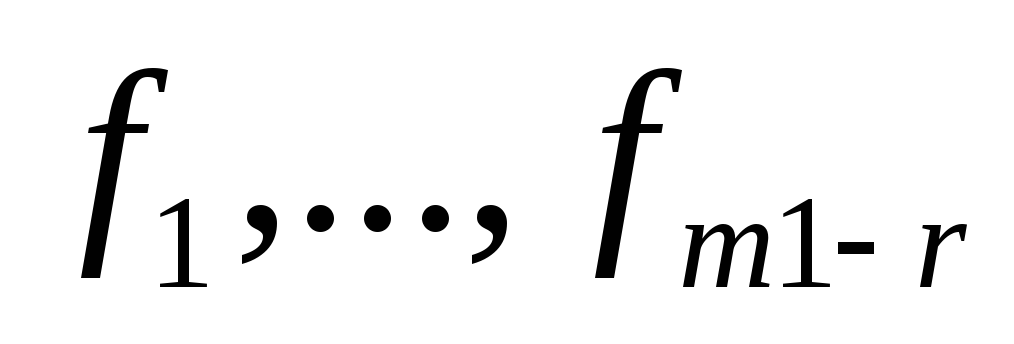
2. Докажем, что этот набор-ЛНЗ

Допустим, что он ЛЗ.

То есть - такие, что комбинация =0

=0

такие, что все

Рассмотрим часть содержащую только

-левая часть лежит в

-правая часть лежит в

так как они равны, то и так и другая часть лежит в пересечении.

Правая часть принадлежит пересечению, следовательно, и левая и правая часть лежит в пересечении.

- следовательно, раскладывается по векторам

т.е.

если перенести, то мы получим

линейную комбинацию базиса=0

следовательно, они все (коэффициенты) равны 0.

следовательно правая часть равна 0, а в левой части базис=0, т.е. все коэффициенты равны 0

следовательно набор - ЛНЗ

Вывод:Мы доказали, что ЛНЗ и что это система образующих, то есть это есть базис суммы.

(- размерность)

ч.т.д.

Примеры

1) В трехмерном пространстве две плоскости не совпадающие, проходящие через начало координат.

dimM₁=2

dimM₂=2

dim(M₁+ M₂­)=3 – сумма -все пространства

2)

12. Пространство матриц (2х2)

L=M₂(R)

пространство верхних треугольных матриц

dimM₁= dimM₂=3

M₁+ M₂­=M₂(R)

dim(M₁+ M₂­)=4

3+3=2+4

2.4

Факторпространство.

Отношение эквивалентности.

M-множество, на нем есть некое отношение – берем 2-а эквивалента рассматриваем упорядоченные пары, для каждой пары говорим, что они находятся в отношении

a<b (a~b)– В этом случае говорим, что находятся в бинарном отношении (делятся или нет, меньше или больше) – это можно сказать для каждой пары.

Свойства бинарного отношения:

1. Рефлексивность: a~a

(делимость – рефлексивность, любое число(? ) на само себя)

2. Симметричность: a~bb~aеслианаходится в отношении сb, тоbнаходится в отношении са. (делимость несимметричность -- но) равенство – симметричность.

3. Транзитивность a~b, b~c – тогдаa~c.

Примерa=b,b=c, a=c– равенство.

меньше a>b, b>c, a>c

Если бинарное отношение обладает всеми тремя бинарными свойствами, то оно называется отношением эквивалентности.

Пример

1) ~ - это равно

тогда, это отношение эквивалентности

2) (modm)

два числа aи b сравнимы по модулюm, если их равенствоm

1) - рефлексивность

2)

3)

- свойство транзитивности то есть это отношение эквивалентности.

Теорема:

Пусть есть M, и на нем задано ~ - отношение эквивалентности.

Рассмотрим для каждого рассмотрим множествов него входят все элементыy изM, которые находятся сx~yв отношении.

Тогда M_xиM_f, то возможны только две ситуации взаимного расположения:

1)_­либо они не пересекаются

2) либо

Доказательство:

M_xиM_f­предположим, что они пересекаются, докажем, что они совпадают, то есть

- это означает по определению множеств, что:

x~zиt~zно поскольку есть соотношение симметричностиx~zt~zследовательно x~t=>

т.е. то и всет.е. одно из этих множеств содержится в другом.

Аналогично доказывается, что

Следствие:Всякое отношение эквивалентности, на множестве, порождает разбиение этого множества, на непересекающиеся подмножества эквивалентных между собой эквивалентов. Эти подмножества называютсяклассы эквивалентности

Пример:

{-30,3,6,…}

{-5,-21,4,7,…}- классы эквивалентности

{-1,2,5,8,…}

никакие классы не пересекаются.

Множество классов эквивалентности называется фактор множества, а переход от исходного множества к множеству классов называется факторизацией по заданному отношению эквивалентности.

Определение:

L –линейное пространство над полемK,,M- подпространство.

Введем ~ отношение эквивалентности на L:

и говорим, что ониa~bесли(- проверить, что это отношение эквивалентности)

Это отношение эквивалентности и фактор множества по заданному соотношению называется фактором пространства LподпространствомM

L/M

Пример

Пространство вектора на плоскости

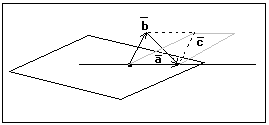
M_x-классы эквивалентности

Лемма:

Если на множестве классов эквивалентности ввести операции по следующему правилу:

- класс суммы.

класс произведения.

Относительно вводимых операций мы получим множество, которое является линейным пространством над тем же полем.

Доказательство:

Мы должны доказать, что результат операции зависит от класса, а не от его представителей

пустьэто означает, что

нужно показать, что это тот же класс, то есть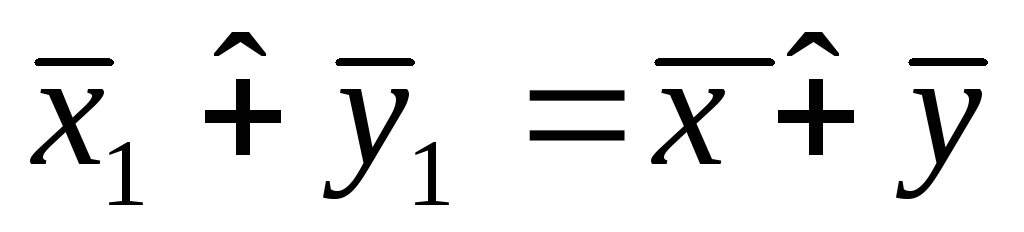

=>

+

=>

------------------

эта разность принадлежит Mт.е.

Вторая часть доказательство умножение на скаляр. ч.т.д.

Отсюда следует, что все аксиомы (свойства операций) Линейного пространства выполняются в фактормножестве.

Пример:

a)

Пространство векторов на плоскости все вектора свободные и выходят из начала координат все вектора лежащие наMобразуют подпространство.

Z- множество всех векторов на плоскости.

M– является классом эквивалентности (по определению)

класс нуля -

все вектора

конец проходит через конец

вектор - это все вектора, концы которых лежат на этой прямой.

Пример:

b)

L=P₃- многочлен степени не выше 3.

многочлены степени не выше первой

фактор пространства.

L/M LпоM

Пусть его

g~fт.е.- старшие степени у них совпадают

старшие члены одинаковые.

Как связаны размерности фактор пространства и исходного множества.

Лемма

пусть, тогда

Доказательство:

Пусть базис пространстваMдополним его до базисаL

такие, что,- базисLто тогда каждый

- может быть записан как линейная комбинация

Теорема:

- подпространство.

Тогда равносильны следующие утверждения:

1) всякий элемент единственным образом можно записать единственныеa,b, что

2) пересечения

12 если есть условие единственности, то пересечение =0.

Предположим, что пересечение содержит какой-то элемент.

Пусть (тогда )

Возьмем любой

Тогда (1) , но у нас есть и он лежит в

и мы получаем противоречие единственности следовательно

21

Пусть , тогда докажем 1

1. По определению, так как xэлемент суммы, то такое представление существует и доказывать надо только единственность.

x=a+bдокажем единственность.

Пусть не так – оно не единственное.

Пусть : x=a₁+b₁=a+b a-a₁=b₁-b a-a₁ b₁-b

Эти две разности лежат в пересечении.

a-a₁ ,b₁-b и следовательно они .a-a₁ b₁-b т.е. представление единственное ч.т.д.