3 Операторы изометрии в пространствах малых размерностей (1,2)

1. а) U dimU=1 (комплексная плоскость)

скалярное произведение<x , y>=xy

базис образует не нулевое число е- базис любой линейный оператор действует как умножение на число.

Ае=e

xU x=e Ax = e = x

по 1 из теоремы: <x , x> = <Ax , Ax> = <x , x> = <x , x>

<x , x>(1-) = 0 (т.к.1-) x



в одиночном унитарном пространстве – это умножение на число ????, модуль которого равен 1

б) Е dimE=1 - || - || - || -

только<x , x> = <Ax , Ax> = <x , x>

²=1 =(+|-)1

либо тождественное отображение, либо отображение относительно начала координат.

2. а) Е dimE=2 ортонормированый базис е₁ , е₂

тогда матрица оператора ^tAA=E (по т. п.4)

=

^tA=a²+c²=b²+d²=1

ab+cd=0

a=cosc=sin b=cosd=sin

cos()=0

n, nZ

1. => cos= - sin

sincos

A=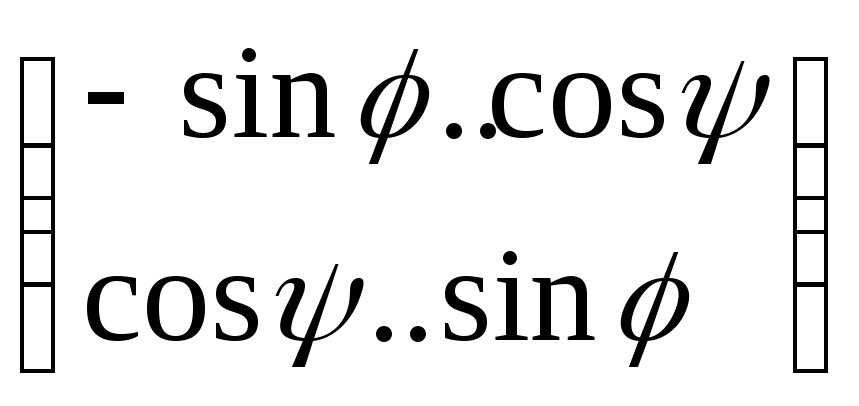

|A|=(+|-)1 = ad – bc = cos+ ????? = sin()

1. |A|=1

sin()=1 Z

 

a=cos b= - sin

c=sin d= cos

 плоский поворот на угол

б) sin() = -1



a=cos b=sin

с=sin d= - cos

A=

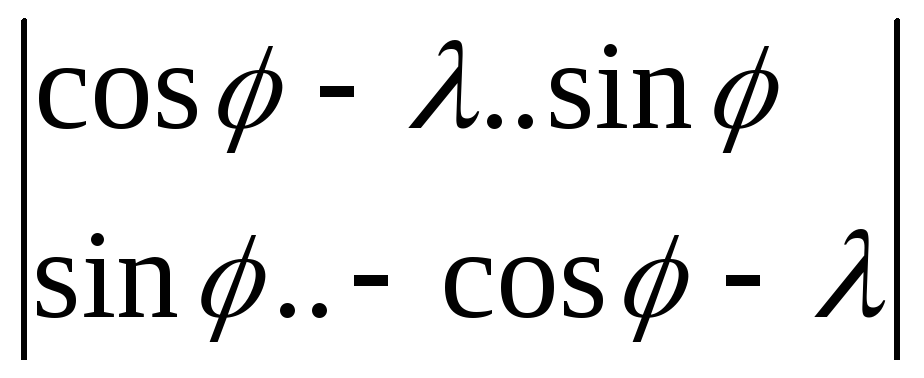=- 1 отражение относительно прямой

(+|-)1

оператор диагонализуется.

Задача проверить, что собственные вектора ортогональны.

4 Структура ортогонального и унитарного операторов.

Теорема:а) А: Е -> E

Операторов изометрии в Е (или ортогональный оператор), тогда существует ортонормированый базис е₁… е₂– ортонормирован, в котором матрица оператора имеет следующий вид:

А=Е_k(s)-един. разм к(s) А_j=

3. Если А: U -> U

Унитарный оператор (унитарная изометрия), то существует ортонормированый базис в котором матрица А:

A=diag(₁, … ,_n) |_k|=1

4. Если х,у собственные вектора отвечающие различным собственным числам, то они ортонормированы <x , y>=0

Доказательство:

Пусть x,y – собственные вектора Ах=x Ay=y 

Т.к. это оператор изометрии:

<x , y> = <Ax , Ay> = <x , y> = <x , y>

<x , y>(1-)=0 т.к. ||=||=1

следовательно

тогда <x , y>=0 т.е. они ортогональны.

3. для U

A: U -> u когда С => - собственное число.

L₁ = Z{e₁} – линейная оболочка в С₁ и е₁-обственный вектор||=1

Рассмотрим ортогональное дополнение

U=L₁L₁^ положим, чтоL₁^ - ортогональное инвариантное.

Если мы берем вектор из L₁^ и применяемA=y A(L₁^) L₁^

<y , e₁>=0

<Ay , Ae₁>=<y , e₁>=0 т.к А – изометрия, то

<Ay , e₁>=₁<Ay , e₁>=0

<Ay , e₁>=0

следовательно Ау L₁^

т.е.L₁^- инвариантно и мы можем рассмотреть ?????? в А и доказывать по индукции.

3 для Е А:Е тогда существует ортонормированный базис:

A_e^e= где матрица А() – матрица плоского поворота.

В этом случае мы не можем утверждать что есть собственное число.

а) если есть с.ч. () как вU (2)

б) пусть собственного числа нет, тогда

(над полем вещественного поля любое пространство имеет инвариантное подпространство размерности 2)

L₁ A(L₁)L₁ dimL₁=2

в L₁ A действует как плоский поворот. Рассмотрим его ортогональное дополнение.

E= L₁L₁^, рассмотрим ортогональное дополнениеL₁^

т.е. если xL₁ ,y L₁^ , то их скалярное произведение =0

<x , y>=0

Доказать нужно, что<x , Ay>=0

Берем любой xL₁ A-поворот, значитx zL₁ такой, что Ах=Z.

<x , Ay>=<Az , Ay>=<z , y>=0

по свойству изометрии. Из<z , y>=0 => zL₁ & yL₁^

т.е. <x ,Ax>=0

по индукции.