Матрица линейного отображения

выберем базис в каждом пространстве

- базис

- базис

Каждому элементу пространства сопоставляется один набор координат.

Рассмотрим образы всех базисных координат

Сопоставим матрицу A

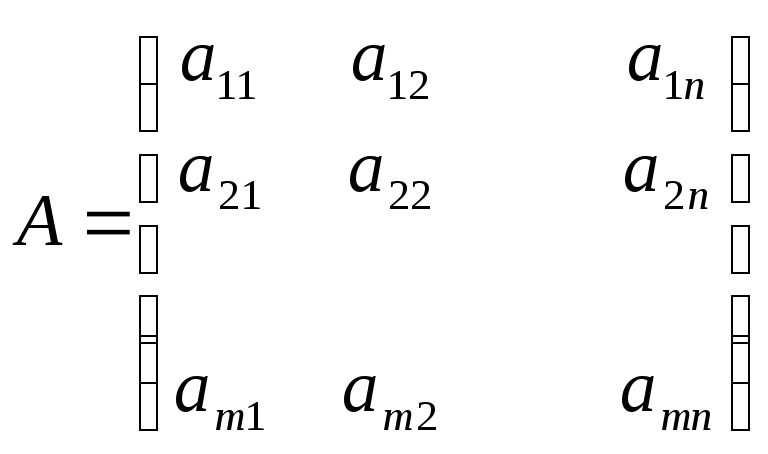
число строк это размерность M, число столбцов это размерностьL

Матрица Аназывается матрицей отображения в базисеeиg

Обозначение

Матрица линейного отображения: столбцы матрицы линейного отображения – это координатные столбцы образов базисных векторов.

Пример

- базис

Рассмотрим образы всех базисных векторов

4))

Изменение матрицы линейного отображения при смене базиса.

Пусть

- базис и- новый базис

- базис и- новый базис

Известна матрица отображения

Мы хотим найти

И известны матрицы перехода и

§4

Инвариантные пространства линейных операторов собственные числа и собственные вектора.

1)

Определение:

Пусть есть линейный оператор Aкоторый действует вL

M– подпространство пространства

- подпространство.

Пространство Mназывается инвариантным подпространством оператораL, если справедливо соотношение: образM лежит вM.

Пример:

линейное пространство многочленов

оператор дифференцирования, тогда инвариантным является подпространство

Теорема:

- инвариантное подпространство оператораAэто условие равносильно тому, что существует такой базис пространстваL, в

Пусть - базисLв котором матрица имеет вид

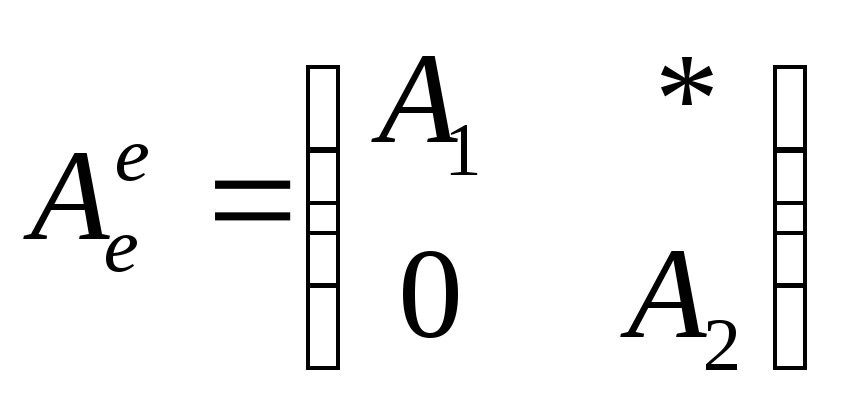гдеr– это размерность пространстваM

- базисM

Доказательство:

1) - базисM

Любой линейно независимый набор можно дополнить до базиса L:

- базиси рассмотрим, как выглядит матрица перехода в этом базисе.

следовательно

тогда матрица оператора

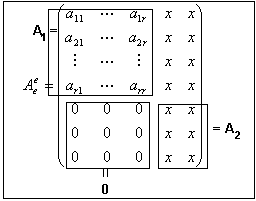
ч.т.д.

2) Следовательно в обратную сторону

Доказать, что есть пространство M-размерностиrинвариантное относительно этого поля.

Возьмем.

- первые базисные вектора.

- их линейная оболочка

а) это линейная оболочка r– линейно независимых векторов

b) докажем, что оно инвариантно: каждый образ элемента, этого пространства лежит в пространстве.

т.е. образы всех базисов лежит в M

2))

Ядро и образ линейного оператора.

Определение:

, тогда его ядром

это множество тех векторов пространства L, которые операторомAпереводятся в 0.

Примеры

1)

2) А– проектирование пространствана плоскостиX0Y

Свойства ядра:

Лемма:ядро всякого оператора – это инвариантное подпространство.

Доказательство.

1) Если , то их линейная комбинация так же лежит в ядре. Рассмотрим

2) Образ ядра – это 0.

ч.т.д.

Определение:

Образ – это множество всех образов, образ оператора A:ImA– это множество всех векторов из пространстваL, которые могут быть записаны как образы Каши (?) либо элементов

ПримерДифферен.образ-

1)

2) оператора проектирования

Лемма:

Образ линейного оператора инвариантное подпространство.

= инвариантное подпространство

Доказательство:

1) рассмотрим

Если 2 элемента лежат в образе, то их линейная комбинация лежит в образе.

2) Докажем, что это подпространство инвариантно.

3) Лемма:размерность ядра и образа линейного оператора.

, dim A=n,

тогда n=m+r

Доказательство.

Зафиксируем какой-нибудь базис

- базис

построим матрицу оператора в этом базисе

- матрица

среди векторов ;r –ЛНЗ следовательно …

Вектора порождают образы – это система образующих, тогда в-r– ЛНЗ столбцов следовательно.

рассмотрим ядро.

2) Xe=0

=rang rпространство решенийn-r системы размерность

эта размерность и есть размерность ядра m=n-r

==

- базис каждому

y=Ax

ImAтогда соответствует

- это линейные комбинации столбцов матрицыА

3))