Линейная алгебра. Линейное пространство, базисы, координаты.

§1

1))

1. Поле- это такое множество, содержащее не менее двух элементов, в котором определены две операции:сложениеиумножение.

Свойства

1. Коммутативность: b+a=a+bab=ba

2. Ассоциативность: (a+b)+c = a+(b+c) , a(bc)=(ab)c

3. Дистрибутивность: a(b+c) = ab+ac

4. Существует () нейтральный элемент «0» :a+0=a

Существует () нейтральный элемент «1» :a^.1=a

5. Для каждого aсуществует () (-a) ,a+(-a)=0,a0 существует ()a^-1,

Множество называется полем, если выполняются все перечисленные свойства.

Пример:

Множество рациональных чисел.

R- комплексные, С- поле-поле

==- это число раз все свойства выполняются.

т.е.- является полем ч.т.д.

Конечное поле.

Рассмотрим множество целых чисел Z.

p- простое число,- множество всех целых чисел которые делятся наp.

- которые дают остаток 1

- все числа дающие остатокp-1

=pZ,

- все числа кратные трем

=3Zдает остаток 0

=1+3Zдает остаток 1

=2+3Zдает остаток 2

+==дает остаток 1

дает остаток 1

+=дает остаток 0

2)). Ключевое определение:Линейное пространство

Определение:

Множество Lназывается линейным пространством над полемkесли в нем определены две операции.

1. сложения 2) умножение на элемент из поля k.

Эти операции подчиняются правилам:

1. коммутативность сложения a+b=b+a

2. ассоциативность сложения a+(b+c) = (a+b)+c

3. ,

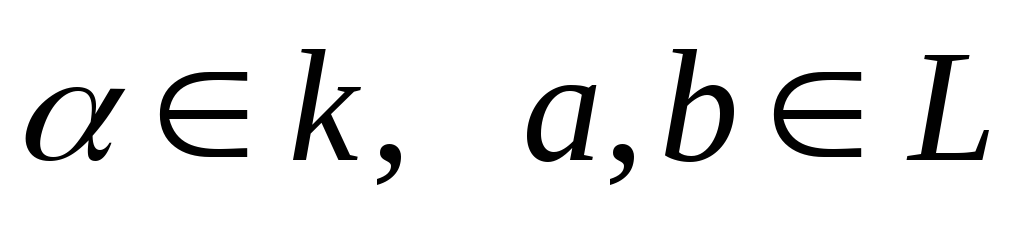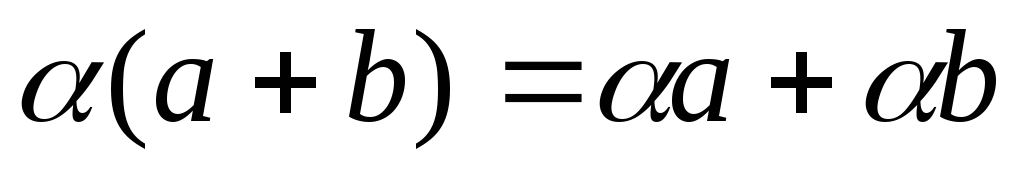
4. ₁k₁ L ,

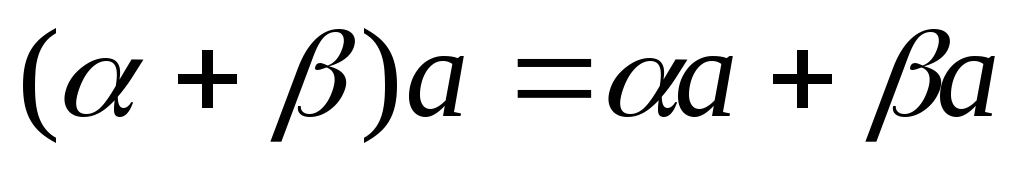
5. ₁k₁ L ,

6. существует нейтральный элемент ()

7. 

8. 

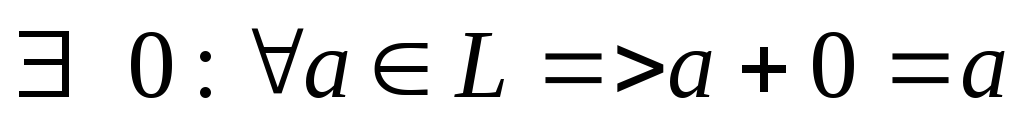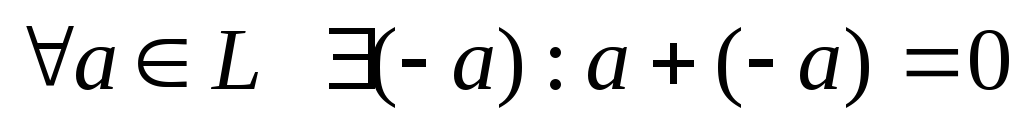
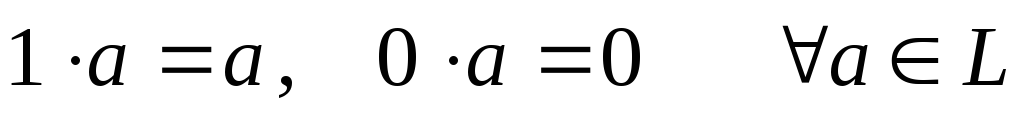
По сложению это абелева группа.

{всеми этими свойствами обладают вектора}

Все свойства линейного пространства полностью совпадают со свойствами векторов на плоскости и в пространстве.

Примеры:

1. Множество векторов на плоскости или в пространстве

2. Арифметическое пространство – это пространство строк и столбцов с элементами из множества вещественных чисел.

- пространство столбцов длиныn.

- пространство столбцов длиныn.

- пространство строк длиныn

! Аналогичные пространства можно рассматривать для любого поля.

3. Пример:

, - это множество всех строчек длины 4

3⁴=81 элемент в этом пространстве.

4) [a,b]- это отрезок на котором определена функция.

[a,b] и рассмотрим множество всех функций лежащих на этом отрезке

L={ f |f:[a , b]  R}(L- множество всех вещественных функций определенных на отрезке [a,b] )

Это линейное пространство лежит над полем L.

Мы можем складывать функцию, умножать на число.

5) Множество всех многочленов коэффициентами из множества R.

- базис бесконечный

это линейное пространство над полем R, если возьмем коэффициент из поляQ- то получим линейное пространство над полемQ.

6)

Базисы и координаты, размерность.

3))

Теорема: Есть пространствоL₁ над полемkи- набор элементов из линейного пространства, тогда равносильны следующие три условия :

! Все определения линейной зависимости и линейной независимости и свойства линейной зависимости и линейной независимости переносятся на любые линейные пространства.

1) - максимальный линейно независимый набор, при добавлении элемента он становится линейно зависимым.

2) - минимальная система образующих

- могла быть записана как линейная комбинацияe

- это свойство теряется при выбрасывании любого элемента – это минимальность.

3)

a)представим как линейную комбинациюe

б) - единственная.

Если выполнено одно из условий, то выполнены и остальные два.

Доказательство 1) из 1следует2

Пусть - максимальнаялинейная независимостьдокажем, что это мин. система образую.

- добавим его к набору

- линейная зависимость

Если он линейно зависим, то есть не все «0», то есть

так как мы получили линейную независимость то все

так как поделим на него,то есть произвольный элемент можно написать через линейную комбинацию, то есть это система образующих.

Докажем, что система минимальна.

Предположим, что он не минимальный и можно выбросить один элемент.

- система образующих

следовательно любой элемент можно написать в виде линейной комбинации и в том числе - то есть он линейно зависим.

так как)

это равенство противоречит ЛН то есть эта система минимальна.

То есть из1следует2

2. из 2следует1если минимально образующей – то это максимально линейно независимый (ЛНЗ) набор.

- не все = 0

пусть , тогдато есть эта система образующих не минимальна, так как один из векторов есть линейная комбинация других, то есть- можно выбросить, и она не минимальна, что не верно.