Определение:

Тогда L( ? ) сумма этих подпространств называется прямой, если выполнено одно из условий теоремы.

Замечание1:Обозначение прямой суммы

Замечание2:если , то говорят, что пространство разложено в прямую сумму подпространств и .

Самостоятельно:

1. Доказать, что если => тогда

2. Е

   

   сли есть тогда /- оператор пространства, еслии , тогда

Таким образом существует взаимно однозначное соответствие с сохранением операций между элементами пространства и фактор пространства /

§3 Линейное отображение линейных пространств.

1)) Определение:

Изоморфизм линейных пространств одинакового размера

Изоморфизм - два множества с какими-то операциями M+,N*0 называются отображение из одного множества в другое, которое обладает свойствами

1) f- взаимно однозначное соответствие (Для каждого элемента существует образ)

2) f- устанавливается отношение между операциями

Примеры изоморфизма:

1) y=lnx- отображение

+

Это взаимно однозначное соответствие

2)

То есть операция умножения ( )сопоставляется операции сложения (+), результат не зависит от порядка. Логарифмическая функция осуществляет изоморфизм двух групп: по

и по +.

Изоморфные алгебраические структуры, обычно рассматриваются как одинаковые, не различимые. L- линейное пространство над полем k . Операции:

1) сложение

2) умножение на число

Теорема:

Пусть M и L два линейных пространства одинаковой размерности, над одним и тем же полем k. , тогда они изоморфные

Доказательство:

Если пространство конечное, то в каждом из них есть базис n

базис в

базис в

построим отображение f из следующим образом по след общему правилу если x равен , то

Нужно проверить, что такое отображение -изоморфизм.

1) Взаимно однозначное соответствие.

- определен, единственным образом.

Каждый элемент линейного пространства, однозначно определяется своим набором координат ( у каждого x-один образ, у y-один прообраз)

2) Что он сохраняет операции.

Пусть а, тогда по определению

по определению отображениеf

мы показали, что линейные поля равные размерности изоморфны ч.т.д.

2))

Определение и примеры линейных отображений линейных пространств.

Определение:

Пусть Mи L-два линейных пространства, над полем kпостроим отображение

- называется линейным отображением, если выполняются свойства:

1) Образ суммы равен сумме образов

2) Если элемент пространства умножается на скаляр, то его образ тоже умножаетсяна скаляр:

Гомоморфизм - это однородность, подобие структур:

1) сохранялись операции

2) но не обязательно взаимно однозначное соответствие

1) отображение «на» - сюръекция

2) отображение«в» - (без склеивания)инъекция

3) изоморфизм блекуция

1

2 у каждого элемента не более одного прообраза.

3

Лемма: если f-линейное отображение, то образ 0-го элемента это 0-ой элемент.

Доказательство:

Возьмем тогда применим это к линейному отображению, что это гомоморфизм.

если все пространство Mотображаетсявнуль,тоивсевнуль,если существует то .

Примеры

1) Фиксированная функция K(x,y)заданная на квадрате [a,b]x[a,b]

Пусть M-множество непрерывных функцийна отрезке [a,b]

всякой функции -сопоставим

а) линейная операция

b) умножение аналогично

Интегральные операторы

2)

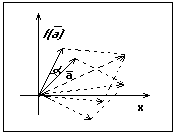
сопоставим каждому вектору результат его поворота вокруг на - фиксированный угол.

- поворот векторана угол

это тоже линейное отображение

1. сумма переходит в сумму

сумма повернется на это линейное отображение.

3)

При умножении вектора на число равносильно умножению проекции на число, при сложении векторов = сложение проекций.

4) Оператор дифференцирования.

5) Матрица

пространство столбцов длинныm

Если LиMсовпадаютотображение- линейный оператор.

3)