5O Положительно определенные квадратичные формы.

Определение: квадратичная форма Q(x₁,x₂,..,x_n) называется положительно определенной, если значения строк положительны на любомненулевом наборе переменных. Аналогично определяется отрицательная определенная форма, неотрицательная и неположительная определенные формы:

Q(x₁,x₂,..,x_n) < 0 – отрицательная

Q(x₁,x₂,..,x_n) >= 0 – неотрицательная

Q(x₁,x₂,..,x_n) <= 0 – неположительная.

Если форма принимает значения разных знаков, она называется неопределенной.

Простейшие свойства положительных определенных форм:

1. Закон инерции. При любом способ приведения ее к диагональному виду все коэффциенты положительны (при квадратах) и нооборот (сумма квадратов с положительными коэффициентами = 0).

2. Сумма двух положительных определенных форм от одних переменных по определению Q₁(x₁,x₂,..,x_n) + Q₂(x₁,x₂,..,x_n)… > 0.

Следствие: сумма матриц A₁,A₂ – матр. Q₁,Q₂, тогда A₁+ A₂ – матр. Q₁ + Q₂

Все собственные числа матриц A₁,A₂– положительно определенные. У их суммы A₁+A₂– собственные числа положительны.

Теорема: Критерий Сильвестра.

Квадратичная форма Q положительно определена тогда и только тогда, когда строго положительны все главные миноры матрицы этой формы.

Q(x₁,x₂,..,x_n) = ^tXAX, A – квадратично симметрична

A₁ = a₁₁

А = …..

A_n =A

Доказательство: Всякую квадратичную форму можно преобразовать к диагональному виду  X= СY – переводит квадратичную форму в

 диагональную

Y = C^-1X,

Q(x₁,x₂,..,x_n) = Q(y₁,y₂,..,y_n) = a₁y₁²+a₂y₂²+…+a_ny_n² (a_i < 0, a_i) x₁

,будем приравнивать к нулю все переменные, кроме первой X = 0

0. ,

тогда получимQ(x₁…0) = a₁₁x² = a_ky_k² a₁₁… a_1n

A = a₂₁… a_2n

a_n1… a_nn

L₁L₂…L_n = Rⁿ L₁ = {l₁…l_n}, полагая x_i  0 получаем L₁, если x₁,x₂  0, получаем L₁L₂ .Рассмотрим цепочку C^-1L₁ C^-1L₂ … C^-1L_n = Rⁿ, т. к. Преобразования невырождены получаем: для y₁ C^-1L_1, для y₂ С^-1L₂

^tCAC = D – это верно C²A= a₁…a_n

^tC_iA_iC_i = D_i C²A_i= x₁…x_i , т. к. a_i > 0_­

x₁

.. - получим определитель и, следовательно, A_i= 0.

A_i = x_i

0

0

6^o Теорема: Q₁(x₁,x₂,..,x_n) … Q₂(x₁,x₂,..,x_n) Q₁ положительно определена – тогда существует инвариантное преобразование, которое приводит форму Q₁ к чистой сумме квадратов: X = CY;

Q₁(x₁,x₂,..,x_n) = y₁² + y₂² + …+ y_n²; а Q₂(x₁,x₂,..,x_n) = a₁y₁² + …+ a_ny_n²;

Следствие: Если есть 2 матрицы А и В – симметрические или эрмитовы, одна из них положительноопределенная А>0, тогда существует невырожденная матрица С ,С 0, такая что ^tСАС = Е, то ^tСВС = diag(a₁…a_n).

Доказательство:Всякую форму можно привести к диагональному виду

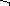X = C₁Z Q(x₁,x₂,..,x_n) = Q₁(x₁,x₂,..,x_n) = d₁z₁²+d₂z₂²+…+d_nz_n² , где все d_i > 0 i . Введем еще замену u_i = z_id_i , тогда u₁² + …+u_n²  в чистую

1/d₁ … 0

сумму C₂ = 0 .. 0 X = C₁C₂U – эти замены переводят Q­₁ в чистую

0 … 1/d_n сумму квадратов

обозначим через В₂ матрицу квадратичной формы после перехода к U :

В₂ = ^t(С₁С₂)B(C₁C₂) – эта симметрическая матрица самосопряженная.

Сществует ортогональная матрица С₃ такая, которая переводит матрицу B₂ в диагональную: ^tC₃B₂C₃ = diag(a₁…a_n); U = C₃Y; X = C₁C₂­C₃Y- -от пременных U переходим к Y, а она преходит к единичной: ^t(С₁С₂)A(C₁C₂) = E; далее:

^tC₃^t(С₁С₂)A(C₁C₂)C₃ = E = ^t(C₁C₂C₃)A(C₁C₂C₃) – она преводит матрицу А в единичную, а матрицу В в диагональную.