vk.com/club152685050 | vk.com/id446425943

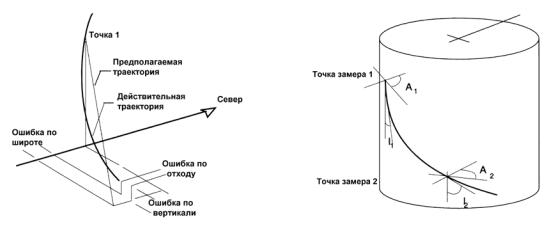
Сбалансированный тангенциальный метод

Это попытки большего приближения к реальной форме ствола при помощи учета результатов замеров не только текущего, но и предыдущего.

В этом методе курсовая длина между двумя последовательными замерами делится на две равные прямые линии.

Таким образом, если А1 и I1 - соответственно азимутальный угол и угол наклона, при предыдущем замере, то :

Основная причина более высокой точности сбалансированного тангенциального

метода состоит в том, что при вычислении конфигурации ствола скважины, меняющей наклон и направление, погрешности текущего вычисления компенсируются последующим.

На участке набора угла ошибки стремятся завысить значения TVD и уменьшить величину горизонтального смещения.

Несмотря на то, что его точность сравнима с точностью метода среднего угла, обычно этот метод не применяют достаточно широко из-за его более сложных формул.

Метод среднего угла

Этот метод просто усредняет углы наклона и азимута двух последовательных точек замера. (рис.4-3). Затем предполагают, что длина участка скважины равна расстоянию между этими двумя точками.

Section

При условии не очень большого расстояния между точками замера по сравнению с кривизной ствола, этот метод позволяет легко, но и с достаточной степенью точности вычислять координату ствола скважины.

vk.com/club152685050 | vk.com/id446425943

Радиус кривизны

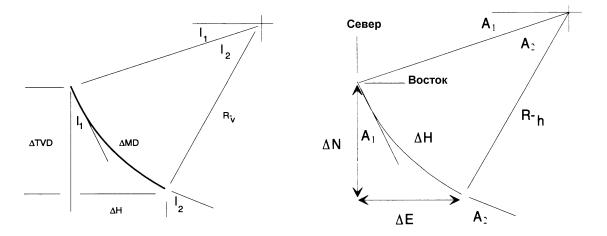
Существо этого метода состоит в подборе цилиндра таких размеров при которых можно было бы две точки замера расположить на его поверхности так, чтобы участок ствола скважины был изогнут в вертикальной и горизонтальной плоскостях и лежал на поверхности этого цилиндра.

(см. рис. 4-4).

Вертикальная проекция

Проведя вертикальную плоскость через кривую пути ствола скважины так, что точки замера 1 и 2, а также участок ствола скважины окажутся на поверхности этого цилиндра (см.рис.4-5). Длина кривой окажется равной MD, радиус окружности цилиндра определяется изменением направления (изменением углов А1 и А2). Углы I1 и I2, как показано на рис. 4-16, - углы набора угла.

Выражая углы I и А в градусах, найдем радиус:

Rv = 180 * 180* ∆MD * [(I2 -I1)*π]-1

∆H = Rv(cosI1-cosI2)

Горизонтальная проекция

Для определения отхода на север и восток, необходимо рассмотреть горизонтальную проекцию участка ствола, лежащую на радиусе Rh (cм. рис. 4-6).

Аналогично выводам для вертикальной проекции, получаем:

Rh = 180 ∆H [ π (А2-А1)]-1

так, что :

∆North = Rh(sinA2-sinA1)

∆East = Rh (cosA1-cosA2)

Точность. В тот время как метод среднего угла достаточно точен при малой кривизне и не большом расстоянии между точками замера, метод радиуса кривизны хорошо подходит и в случаях при большом расстоянии между точками замера и больших кривизнах ствола

vk.com/club152685050 | vk.com/id446425943

Метод минимальной кривизны

Этот метод эффективно заменяет

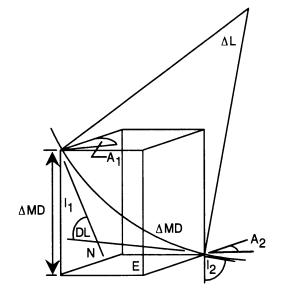
участок реальной кривой ствола между двумя точками замера сферической дугой. Т.е. требуется найти пространственный вектор, который определяется углами наклона и направления в каждой из двух точек замера и который плавно соединял бы дугу с этими точками при помощи фактора отношения, определяемого кривизной участка ствола (см.рис. 4-7).

Этот метод - один из наиболее точных в определении положения ствола скважины.

Кривизна (Dog-leg)

DL = cos-1[cos(I2-I1) - sinI1sinI2(1 -

cos(A2-A1)]

Рисунок 4-7

Фактор отношения (RF)

Курсовая длина MD измеряется вдоль кривой, в то время как I и А определяют направления прямых линий в пространстве. Необходимо совместить эти прямые с сегментами кривой при помощи фактора отношения, определяемого как:

RF = 360 tan (DL/2) [ DL/π ]-1

или

RF = 360*(1 - cosDL) *[ DL*π *sinDL ]-1

Где DL выражается в градусах. Для маленьких углов (DL <.0001), RF полагают равным 1. Затем мы можем определить увеличение по трем осям для определения следующей точки замера

∆TVD = (∆MD/2) (cosI1+cosI2) RF

∆North = (∆MD/2) (sinI1cosA1+sinI2cosA2) RF

∆East = (∆MD/2) (sinI1sinA2+SinI2sinA2) RF

На сегодняшний день метод минимальной кривизны - наиболее точный. Именно его Анадрилл выбрал в качестве расчетного.

Метод Меркюри

Свое название он получил по месту первого применения в Меркюри, Невада, при бурении шахты для испытания атомной бомбы. В нем скомбинированы тангенциальный и сбалансированный тангенциальный методы и учитывается длина измерительного прибора. (STL). В нем, та часть измеряемой кривой, где находится измерительный прибор, рассматривается как отрезок прямой линии, а остальная часть кривой рассчитывается сбалансированным тангенциальным методом

∆TVD = [ (∆MD - STL)/2 ] *(cosI1+cosI2) + STL*cosI2 ∆North = [(∆MD-STL)/2](sinI1cosA1+sinI2cosA2) + STL sinI2cosA2 ∆East = [(∆MD-STL)/2](sinI1sinA1 + sinI2sinA2) + STL sinI2sinA2

vk.com/club152685050 | vk.com/id446425943

Относительная точность различных методов

Предположим, что существует скважина, пробуренная в направлении на север длиной 2000’ MD cо скоростью набора угла 3/100’ и расстояниями между замерами параметров в 100’. Можно вычислить относительную точность различных методов. Сравнивая с “действительной” TVD, равной 1653,99’ и отходом на север в 954,93’ мы находим следующее.

Ясно, что это лишь показатель относительной точности и наиболее предпочтительным оказывается тот метод, который представляет ствол скважины в виде серии сегментов длин окружностей. Действительный профиль скважины может не совпадать с вычисленным.

Необходимо отметить, что в приведенном примере не рассматривалось изменение азимутального угла, хотя его следовало бы учесть при оценке точности расчетов. Однако, совершенно очевидно, что учет и этого параметра только лишь еще больше увеличит расхождения в вычислениях трехразмерного случая.

Интенсивность

Интенсивность является мерой изменения величины наклона и/или направления ствола скважины. Обычно она выражается в градусах на 100 футов или в градусах на 10 или 30 метров.

Для вычисления суммарного эффекта как изменения направления, так и наклона между точками замера применимы несколько формул:

d = DLS интервал

I1 = Наклон в 1 точке замера A1 = Азимут в 1 точке

I2 = Наклон во 2 точке A2 = Азимут во 2 точке

формула, применимая во всех случаях:

1. DLS = (d/∆MD)2sin-1{[(sin∆I/2)2 + (sin∆A/2)2 * sinI1sinI2]}1/2

для тангенциального метода .

2. DLS = (d/∆MD)cos-1 [(sinI1sinI2)(sinA1sinA2+cosA1cosA2)+(cosI1cosI2)]

для модели минимальной кривизны.

3. DLS = (d/∆MD)cos-1[cos∆I - (sinI1sinI2)(1 - cos∆A)]

Все три уравнения идентичны тригонометрически и можно пользоваться любым из них. Необходимо только иметь в виду, что вычисление косинусов при малых углах значительно труднее, чем синусов если нет специальных вычислительных средств.

Таблица 4-1