Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

аэродинамики и гидромеханики.pdf

Скачиваний:

Добавлен:

31.08.2019

Размер:

25.4 Mб

Скачать

☆

1 / 321 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

НАСОСЫ. ВЕНТИЛЯТОРЫ. КОМПРЕССОРЫ.

№1. Насос перекачивает 30%-ную серную кислоту. Показание манометра на нагнетательном трубопроводе 1,8 кгс/см2, показание вакуумметра (разрежение) на всасывающем трубопроводе перед насосом 29 мм рт. ст. Манометр присоединён на 0,5 м выше вакуумметра. Всасывающий и нагнетательный трубопроводы одинакового диаметра. Какой напор развивает насос?

1) Т. к. диаметры всасывающего и нагнетательного трубопроводов одинаковы, то в соответствии с формулой (1.17) равны и скорости потоков в них:

Q = W·S = W π d 2	; W =	4 Q	.

4		π d 2

2) Напор, создаваемый насосом, находим по формуле (2.2):

H =

P − P

+ Ho +

W 2

−W 2

вс

;

ρ g

H =

(P + P ) − (P − P )

+ Ho +

W 2

−W 2

атм

ман

атм

вак

вс

;

ρ g

H =

+ P

+ Ho

W 2 −W 2

ман

вак

вс

;

ρ g

плотность 30%-ной серной кислоты найдём по таблице III:

ρ = 1220 кг/м3;

H = 1,8 9,81 104 + 29 133,3 + 0,5 =15,6 м . 1220 9,81

№2. Насос перекачивает жидкость плотностью 960 кг/м3 из резервуара с атмосферным давлением в аппарат, давление в котором составляет Pизб = 37 кгс/см2. Высота подъёма 16 м. Общее сопротивление всасывающей и нагнетательной линий 65,6 м. Определить полный напор, развиваемый насосом.

vk.com/club152685050 | vk.com/id446425943

Напор, создаваемый насосом, находим по формуле (2.1):

H =	P2 − P1		+ Ho + h			п ;
H =			+ Ho + h			п ;
	ρ g
H =	(Pатм + Pман ) − Pатм						+ Ho + hп ;
H =							+ Ho + hп ;
		ρ g
H =	Pман	+ Ho + hп ;
H =		+ Ho + hп ;
	ρ g
H =	37 9,81 10			4	+16 + 65,6 = 467 м .

	960 9,81
	960 9,81

№3. Определить к. п. д. насосной установки. Насос подаёт 380 дм3/мин мазута относительной плотности 0,9. Полный напор 30,8 м. Потребляемая двигателем мощность 2,5 кВт.

1) Плотность мазута - по формуле (1.2):

ρмаз = ∆·ρв = 0,9·1000 = 900 кг/м3.

2) К. п. д. выразим из формулы (2.3):

= Q ρ g H ;

1000 η

η = Q ρ g H = 380 900 9,81 30,8 = 0,69 . 1000 N 1000 60 1000 2,5

№4. Производительность насоса 14 дм3/с жидкости относительной плотности 1,16. Полный напор 58 м. К. п. д. насоса 0,64, к. п. д. передачи

vk.com/club152685050 | vk.com/id446425943

0,97, к. п. д. электродвигателя 0,95. Какой мощности двигатель надо установить?

1)Плотность жидкости - по формуле (1.2):

ρ= ∆·ρв = 1,16·1000 = 1160 кг/м3;

2)К. п. д. всей установки находим по формуле (2.4): η = ηнас·ηпер·ηдвиг = 0,64·0,97·0,95 = 0,59.

3)Мощность, потребляемую насосной установкой, найдём по формуле (2.3):

= Q ρ g H = 14 1160 9,81 58 =15,66 кВт. 1000 η 1000 1000 0,59

4) Двигатель подбирается так, чтобы был запас мощности на пусковые перегрузки. Коэффициент запаса мощности по таблице 2.1 примем равным 1,17.

Nдвиг = β·N = 1,17·15,66 = 18,3 кВт.

№5. Поршневой насос установлен на заводе, расположенном на высоте 300 м над уровнем моря. Общая потеря высоты всасывания составляет 5,5 м вод. ст. Геометрическая высота всасывания 3,6 м. При какой максимальной температуре воды ещё возможно всасывание?

Теоретическая высота всасывания поршневого насоса определяется по формуле (2.5):

Hвс ≤ А – ht – ∑h.

Наша задача – найти предельное значение давления насыщенного пара воды ht и по его значению – температуру воды.

Предельное значение давления насыщенного водяного пара:

ht = А – Hвс – ∑h.

vk.com/club152685050 | vk.com/id446425943

Атмосферное давление зависит от высоты над уровнем моря. По таблице XIX для 300 м над уровнем моря A = 10 м вод. ст.

ht = 10 – 3,6 – 5,5 = 0,9 м вод. ст.

Температуру воды с использованием значений таблицы 2.2:

Она находится в интервале от 40 до 50 °С. Изменению температуры воды на 1°С соответствует изменение давления насыщенного пара равное

1,25 − 0,75 = 0,05 м вод. ст. Чтобы получить результат нужно решить уравнение:

0,75 + 0,05·X = 0,9;

Х = 3, т. е. температура воды равна:

40°C (этому соответствует 0,75) + 3°C = 43°С.

№6. Определить производительность дифференциального поршня насоса, который имеет больший диаметр ступенчатого плунжера 340 мм, меньший – 240 мм. Ход плунжера 480 мм, частота вращения 60 об/мин. Коэффициент подачи 0,85. Определить также количество жидкости, подаваемой каждой стороной ступенчатого плунжера.

К этой задаче см. пример 2.4.

1) Производительность всего поршня находим по формуле (2.6):

		Q =η		F s n	= 0,85	0,785 0,342 0,48 60				=		м3
											0,037		.
											0,037		.
			υ	60				60				с
2) Количество жидкости, выходящее из правой камеры можно найти так:
		=η	(Fплунжера − Fштока ) s n				=	0,85	0,785 (0,34		2 − 0,242 ) 0,48 60			= 0,0186	м3
Q	мал															.
Q																.
		υ		60							60				с
				60							60				с

То есть малый плунжер выталкивает 0,0186 м3/с жидкости.

vk.com/club152685050 | vk.com/id446425943

3) Количество жидкости, вытесняемой большим плунжером, находим как разность общего количества жидкости и того, что вытесняет малый плунжер:

Qбол = Q – Qмал = 0,037 – 0,0186 = 0,0184 м3/с.

№7. Поршневой насос двойного действия наполняет бак диаметром 3 м и высотой 2,6 м за 26,5 мин. Диаметр плунжера насоса 180 мм, диаметр штока 50 мм, радиус кривошипа 145 мм. Частота вращения 55 об/мин. Определить коэффициент подачи насоса.

1) Производительность найдём как отношение объёма жидкости (т. е. бака) к времени, которое насос затрачивает на его перекачку:

	V		π D2 H		0,785 32		2,6		м3
Q =	бака	=		=				= 0,01155		.
			4 τ			26,5
	τ				60				с

2) Ход поршня равен двум радиусам кривошипа:

s = 2·Rкрив = 2·0,145 = 0,29 м.

3) Коэффициент подачи насоса выразим из формулы (2.7):

Q =	ηυ		(2 Fплунжера	− fштока ) s n
						;
				60

ηυ =			60 Q	=	60 0,01155		= 0,89.

		(2 F − f ) s n			0,785 (2 0,182 − 0,052 ) 0,29 55

№8. Центробежный насос, делающий 1800 об/мин, должен подавать 140 м3/ч воды, имеющей температуру 30 °С. Среднее атмосферное давление в месте установки насоса 745 мм рт. ст. Полная потеря напора

vk.com/club152685050 | vk.com/id446425943

во всасывающей линии составляет 4,2 м. Определить теоретически допустимую высоту всасывания.

Высота всасывания центробежного насоса рассчитывается по формуле:

Hвс ≤ А – ht – hп.вс. – hкав.

1) Атмосферное давление переводим в мм вод. ст.:

А = 0,745 13600 = 10,13 мм вод. ст. 1000

2)По таблице 2.2 находим, что давление насыщенного пара воды при 30 °С равно 0,43 м вод. ст.

3)Кавитационную поправку находим по формуле (см. пункт 5):

2 0,67		140 18002	0,67
hкав = 0,00125·(Q·n )	= 0,00125·		= 3,267 м	.
			= 3,267 м
		3600

4) Высота всасывания:

Hвс ≤ 10,13 – 0,43 – 4,2 – 3,267;

Hвс ≤ 2,2 м, то есть допустима высота всасывания не более 2,2 м.

№9. Центробежный насос при перекачке 280 дм3/мин воды создаёт напор Н = 18 м. Пригоден ли этот насос для перекачки жидкости относительной плотности 1,06 в количестве 15 м3/ч по трубопроводу диаметром 70×2,5 мм из сборника с атмосферным давлением в аппарат с

давлением Ризб = 0,3 кгс/см2? Геометрическая высота подъёма 8,5 м. Расчётная длина трубопровода (собственная плюс эквивалентная длина местных сопротивлений) 124 м. Коэффициент трения в трубопроводе λ = 0,03. Определить также какой мощности электродвигатель нужно установить, если к. п. д. насосной установки составляет 0,55.

К этой задаче смотри пример 2.6.

1)Плотность жидкости - по формуле (1.2): ρ = ∆·ρв = 1,06·1000 = 1060 кг/м3.

2)Скорость жидкости найдём по формуле (1.17): Q = W·S;

W =	4 Q	=	15	=1,256	м	.
	π d 2		3600 0,785 0,0652
					с

vk.com/club152685050 | vk.com/id446425943

3) Напор, создаваемый насосом, находим по формуле (2.1):


H =	P2 − P1		+ Ho + hп ;

	ρ g
H =	(Pатм + Pизб ) − Pатм			+ Ho + hп ;

			ρ g
H =	Pизб	+ Ho + hп .

	ρ g

4) Потери напора находим по формуле:

L + ∑Lэкв

124

1,256

= 1

+ λ

= 1

+ 0,03

= 4,68 м

2 g

0,065

2 9,81

5) Требуемый напор насоса:

H = 0,3 9,81 104 + 8,5 + 4,68 =16 м. 1060 9,81

6) Требуемую производительность насоса переведём в м3/мин:

Q = 15	м3	=	15 1000		= 250	дм3

	ч			60		мин .

7) Точка (280 дм3/мин; 18 м) относится к характеристике насоса, а точка (250 дм3/мин; 16 м) – к характеристике сети. Даже без построения графика можно понять, что точка (250 дм3/мин; 16 м) лежит ниже характеристики насоса, значит, данный насос подходит для выполнения задания.

8) Мощность, затрачиваемую насосной установкой, находим по формуле (2.3):

= Q ρ g H = 15 1060 9,81 16 =1,26 кВт . 1000 η 3600 1000 0,55

9) Двигатель подбирается так, чтобы был запас мощности на пусковые перегрузки. Коэффициент запаса мощности по таблице 2.1 примем равным 1,5.

Nдвиг = β·N = 1,5·1,26 = 1,89 кВт.

№10. Центробежный насос для перекачки воды имеет следующие паспортные данные: Q = 56 м3/ч, Н = 42 м, Q = 10,9 кВт при n =

= 1140 об/мин. Определить 1) к. п. д. насоса, 2) производительность его, развиваемый напор и потребляемую мощность при n = 1450 об/мин, считая, что к. п. д. остался неизменным.

vk.com/club152685050 | vk.com/id446425943

1) К. П. Д. выразим из формулы (2.3):

= Q ρ g H ;

1000 η

η = Q ρ g H = 56 1000 9,81 42 = 0,59. 1000 N 3600 1000 10,9

2) Характеристики насоса при частоте вращения рабочего колеса n2 = 1450 об/мин найдём по формулам (2.8):

а) Производительность:

Q	=	n	; Q2 =	Q n	2	=	56 1450	= 71,2	м3
1		1		1						.


Q2		n2		n1			1140		ч

б) Напор:

Н	1	n		2					H				42
	1	=	1	;	H		=			1		=			= 68 м.
		=		;	H	2	=				2	=		2	= 68 м.
Н2						2		n			2		1140	2
Н2		n2						n					1140
									1
									1

								n					1450
									2

в) Мощность:

	1	n		3								10,9
	1	=	1	;		=			1		=			= 22,4 кВт .
		=		;	2	=				2	=		3	= 22,4 кВт .
2					2		n			2		1140	3
2		n2					n					1140
								1
								1
							n2					1450

или

2	=	Q2 ρ g H2	=	71,2 1000 9,81 68	= 22,4 кВт	– это можно делать
		1000 η
				3600 1000 0,59

только при условии постоянства к. п. д.

№11. При испытании центробежного насоса получены следующие данные:

Q, дм3/мин	0	100	200	300	400	500
Н,м	37,2	38,0	37	34,5	31,8	28,5

Сколько жидкости будет подавать этот насос по трубопроводу диаметром 76×4 мм, длиной 355 м (собственная плюс эквивалентная

длина местных сопротивлений) при геометрической высоте подачи

4,8 м? Коэффициент трения λ = 0,03, SРдоп = 0. (Построить характеристики насоса и трубопровода и найти рабочую точку.)

vk.com/club152685050 | vk.com/id446425943

Как изменится производительность насоса, если геометрическая высота подачи будет 19 м?

Найдём полное гидравлическое сопротивление сети по формуле (1.50):

L + ∑Lэкв

сети

= 1

+ λ

+ H

+ P

;

2 g

доп

L + ∑Lэкв

W 2

L + ∑Lэкв

8 Q2

Рсети

= 1

+ λ

+ Ho

= Но

+ 1

+ λ

2 g

π 2 d 4 g

2) Составляем уравнения характеристик сети:

для высоты 4,8 м

					355				8 Q2
Р = Н			= 4,8+ 1	+ 0,03					1			= 4,8+ 609720,6 Q2
Р = Н		1	= 4,8+ 1	+ 0,03								= 4,8+ 609720,6 Q2
1		1			0,068		3,142 0,0684 9,81					1
					0,068		3,142 0,0684 9,81
для высоты 19 м
					355				8 Q2
Р2	= Н2		=19 + 1	+ 0,03					2			=19 + 609720,6 Q22 .
Р2	= Н2		=19 + 1	+ 0,03	0,068	3,14		2	0,068	4	9,81	=19 + 609720,6 Q22 .
					0,068	3,14			0,068		9,81

3) В этих уравнениях подача выражена в м3/с. Переведём её в дм3/мин:


Н1 = 4,8 +	609720,6		Q12 ;
Н1 = 4,8 +		(60 1000)2	Q12 ;
		(60 1000)2
Н2 =19 +	609720,6		Q22 .
Н2 =19 +	(60 1000)2		Q22 .
	(60 1000)2

4) Для построения графика найдём по этим двум уравнениям напоры для тех же значений подачи, которые используются для построения характеристики насоса:

Q, дм3/мин	0	100	200	300	400	500
Н1,м	4,8	6,5	11,6	20	31,9	47,1
Н2,м	19	21	26	34	46	61

5) Строим графики характеристик насоса и сети Н = f(Q) [синяя];

Н1 = f(Q1) [зеленая];

Н2 = f(Q2) [фиолетовая]:

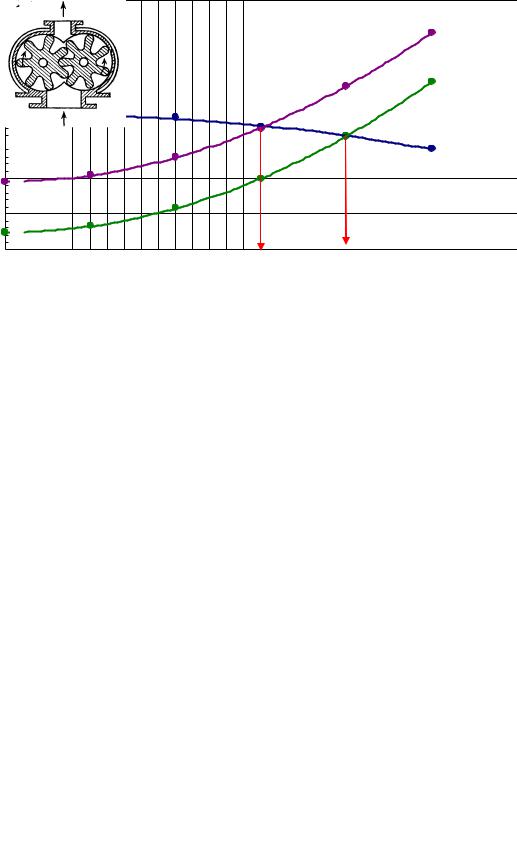
vk.com/club152685050 \| vk.com/id446425943
	70
	60
	50
м
Напор,	40
	30

	20
	10
	0
	0	100	200	300	400	500	600
				Подача, дм3/мин

6) По графику находим рабочие точки – то есть точки пересечения кривой характеристики насоса с кривыми характеристик сетей 1 и 2:

при высоте подачи 4,8 м:

Q1 = 400 дм3/мин = 0,4 м3/мин;

при высоте подачи 19 м:

Q1 = 300 дм3/мин = 0,3 м3/мин.

№12. Определить производительность шестерёнчатого насоса по следующим данным: частота вращения 650 об/мин, число зубьев на шестерне 12, ширина зуба 30 мм, площадь сечения зуба, ограниченная внешней окружностью соседней шестерни, 7,85 см2, коэффициент подачи 0,7.

К этой задаче смотри пример 2.7.

Производительность шестерёнчатого насоса определяется по формуле:

vk.com/club152685050 | vk.com/id446425943

Q =η	2 f b z n		2 7,85 10-4	0,03 12 650		м3		м3
		= 0,7			= 0,004286		= 0,004286 60 = 0,257		.

υ	60			60		с		мин

№13. Требуется выкачивать 215 дм3/мин раствора относительной плотности 1,06 из подвального бака водоструйным насосом. Высота подъёма 3,8 м. Давление воды перед насосом Ризб = 1,9 кгс/см2. К. п. д. насоса 0,15. Сколько кубометров воды в час будет расходовать водоструйный насос?

К этой задаче смотри пример 2.9.

1)Плотность раствора - по формуле (1.2):

ρ= ∆·ρв = 1,06·1000 = 1060 кг/м3.

2)Находим производимую насосом полезную работу (мощность). Здесь используем параметры жидкости:

215 1060 9,81 4

Nпол = Qр·ρр·g·H = =141,6 Вт. 60 1000

3) Затрачиваемую насосом мощность находим уже с использованием параметров воды:

Nзатр = Qв·ρв·g·(Hр - Н).

Выражение ρ·g·(Hр - Н) равно давлению столба воды высотой от уровня жидкости в напорном баке до линии соединяющей центры тяжести сечений, то есть избыточному давлению:

Ризб = ρ·g·(Hр - Н) = 1,9 кгс/см2;

Nзатр = Qв· Ризб.

4)К. п. д. – это отношение полезной мощности к затрачиваемой:

η= пол .

затр

vk.com/club152685050 | vk.com/id446425943

5) Отсюда выражаем расход воды:

Qв =	Nпол	=	141,6	= 0,00506	м3	= 0,00506 3600 = 18,2	м3	.

	η Ризб		0,15 1,9 9,81 104		с		ч

№14. Какой мощности электродвигатель необходимо установить к вентилятору производительностью 110 м3/мин при полном напоре 834 Па (85 мм вод. ст.)? К. п. д. вентилятора 0,47.

Мощность, потребляемую вентиляционной установкой, находим по формуле (2.11):

=	Q P	=	110 834	= 3,2 кВт.
			1000 0,47
1000 η		60

№15. Центробежный вентилятор, делающий 960 об/мин, подаёт 3200 м3/ч воздуха, потребляя при этом 0,8 кВт. Давление (избыточное), создаваемое вентилятором, 44 мм вод. ст. Каковы будут у этого вентилятора подача, давление и затрачиваемая мощность при n =

= 1250 об/мин? Определить также к. п. д. вентилятора.

Назначим индекс «1» параметрам при частоте вращения 960 об/мин, а индекс «2» - параметрам при 1250 об/мин.

1) Подачу найдём по формулам (2.8):

Q	=	n		=	Q n	2	=	3200 1250	= 4167	м3
1		1	; Q2		1						.
					n1
Q2		n2
								960		ч

2) Переведём давление, создаваемое вентилятором в Па:

101300 Па ------	10330 мм вод. ст.
Х ------	44 мм вод. ст.
Х = Ризб = 431,5 Па.
По формуле (2.10):

∆Р1 = Рст.н. – Рст.вс.= (Ратм + Ризб) – Ратм = Ризб.

3) Напор или давление найдём по формулам (2.8):

Р	n		2					Р				431,5
1	=	1	;	Р		=			1		=			= 732 Па .
	=		;	Р	2	=				2	=		2	= 732 Па .
Р2					2		n			2		960	2
Р2	n2						n					960
								1
								1

							n2					1250

4) К. п. д. выразим из формулы (2.11):

vk.com/club152685050 | vk.com/id446425943

1 =		Q1	Р1				;
1 =							;
	1000 η				1
					1
η =	Q1		Р1			=		3200 431,5	= 0,48.
η =	1000 N					=			= 0,48.
1	1000 N			1				3600 1000 0,8
				1

5) Так как при изменении мощности к. п. д. тоже изменяется, рассчитываем её по формулам (2.8):

	1	n		3								0,8
	1	=	1	;		=			1		=			= 1,77 кВт .
		=		;	2	=				2	=		3	= 1,77 кВт .
2					2		n			2		960	3
2		n2					n					960
								1
								1

							n2					1250

№16. Какое количество воздуха будет подавать вентилятор примера 2.12 при работе на сеть, у которой при расходе 1000 м3/ч сумма (SРск + SРтр + SРм.с.) составляет 265 Па, а разность давлений в пространстве нагнетания и в пространстве всасывания равняется 20 мм вод. ст.?

Наша задача найти уравнение характеристики сети, изобразить на графике и найти точку пересечения с кривой характеристики насоса.

В общем случае уравнение характеристики сети имеет вид: ∆Р = а·Q2 + b.

1) Переводим сумму давлений в мм вод. ст.:

101300 Па ----- 10330 мм вод. ст.

265 Па ----- Х

Х = ∆Рск + ∆Ртр + ∆Рм.с. = а·Q2 = 27 мм вод. ст.

2)b = ∆Рдоп = 20 мм вод. ст.

3)Составляем таблицу для точек характеристики сети:

Q, м3/ч	а·Q2	∆Р, мм вод. ст.
1000	27	47,00
1000/1,25 = 800	27/1,252	37,28
1000/2 = 500	27/22	26,75
1000/2,5 = 400	27/2,52	24,32
1000/5 = 200	27/52	21,08
1000/10 = 100	27/102	20,27
0	0	20,00

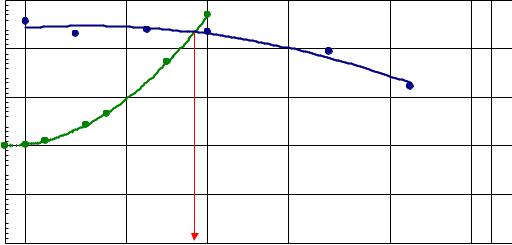
vk.com/club152685050 \| vk.com/id446425943
4) Строим график, данные характеристики вентилятора [синяя] берём из
примера 2.12 в мм вод. ст.
	50
	45
вод.ст.	40
	35
	30
мм	30
мм	25
Напор,	20
	15
	10
	10
	5
	0
	0	500	1000	1500	2000	2500
			Подача, м3/ч

По графику находим, что рабочей точке соответствует подача Q = 940 м3/ч.

№17. Сколько воздуха будет подавать вентилятор примера 2.12 в сеть, у которой при расходе 1350 м3/ч сумма (SРск + SРтр + SРм.с.) составляет 167 Па, а SРдоп равно 128 Па?

В общем случае уравнение характеристики сети имеет вид:

∆Р = а·Q2 + b.

1)∆Рск + ∆Ртр + ∆Рм.с. = а·Q2 = 167 Па.

2)b = ∆Рдоп = 128 Па.

3)Составляем таблицу для точек характеристики сети:

Q, м3/ч	а·Q2	∆Р, Па
1350·1,5 = 2025	167·1,52	503,75
1350	167	295,00
1350/1,5 = 900	167/1,52	202,22
1350/2 = 675	167/22	169,75
1350/2,5 = 540	167/2,52	154,72
0	0	128,00

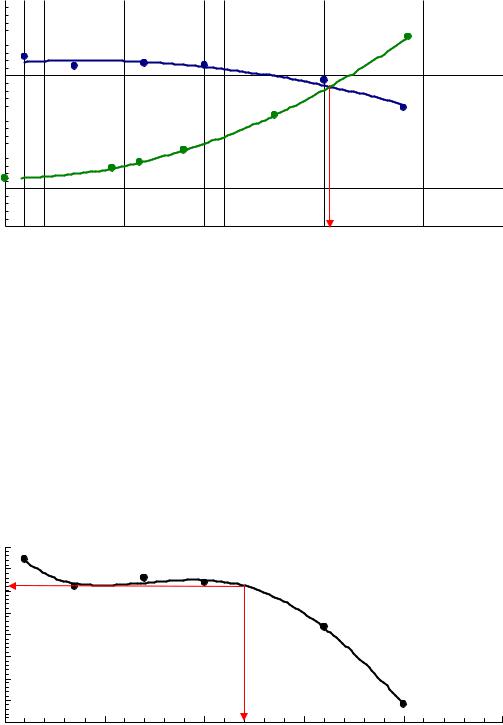
vk.com/club152685050 \| vk.com/id446425943
4) Строим график, данные характеристики вентилятора берём из примера
2.12 в Па.
	600
	500
Па	400
Па
Напор,	300
Напор,	200
	200
	100
	0
	0	500	1000	1500	2000	2500
			Подача, м3/ч

По графику находим, что рабочей точке соответствует подача Q = 1630 м3/ч.
	№18. Какую частоту вращения надо дать вентилятору примера
2.12, если он должен подавать 1500 м3/ч воздуха в сеть, полное
сопротивление которой при этом расходе 422 Па.
Построим график характеристики вентилятора при частоте вращения 1440
об/мин.
	460
	440
Па	420
Па	400
Напор,	400
	380
	360

	340
	320
	300
	0	500	1000	1500	2000	2500
			Подача, м3/ч

В общем случае уравнение характеристики сети имеет вид:

∆Р = а·Q2 + b = 422 Па – это рабочая точка, то есть она принадлежит также и характеристике вентилятора.

vk.com/club152685050 | vk.com/id446425943

По графику находим, что рабочей точке соответствует подача 1200 м3/ч. Назначим индекс «1» параметрам при частоте вращения 1440 об/мин, а индекс «2» - параметрам при искомой частоте об/мин.

Подачу найдём по формулам (2.8):

n1 = 1440 об/мин; Q1 = 1200 м3/ч; Q2 = 1500 м3/ч;

1500 1440

=1800

м3

; n2

1200

№19. Определить аналитическим путём и по T – S диаграмме температуру воздуха после адиабатического сжатия его от начального давления (абсолютного) 1 кгс/см2 до конечного давления 3,5 кгс/см2. Начальная температура 0°С. Определить также затрату работы на сжатие 1 кг воздуха.

1) Температура после сжатия:

а) Аналитически – по формуле (2.14):

			k−1
T		P
			k
2	=	2		;

T1		P1

показатель адиабаты k находим по таблице V: k = 1,4.

Выражаем Т2:

			P
Т		= T	2
Т	2	= T
	2	1	P1
			P1

k−1			1,4−1
k	3,5
				1,4
= 273					= 390 К =117 °С.

		1

б) По T – S диаграмме [хорошую диаграмму для воздуха см. Касаткин А.Г. Основные процессы и аппараты химической технологии - 7-е изд. с. 742]:

Сначала находим точку с координатами 0 °C (273 К); 1 кгс/см2 (1 ата). В адиабатном процессе изменения энтропии не происходит, поэтому от этой точки поднимаемся вверх по линии S = const до пересечения с изобарой

3,5 кгс/см2 (3,5 ата). В этой точке как раз и имеем искомую конечную температуру: T = 390 К = 117 °С.

2) Затрату работы на сжатие 1 кг воздуха находим по формуле (2.12):

k−1

1,4−1

1,4

8310

3,5

Дж

кДж

1,4

L =

R T

−1

273

−1 =117835

≈118

ад

k −1

1,4−1

кг

vk.com/club152685050 | vk.com/id446425943

№20. Определить мощность, потребляемую углекислотным поршневым компрессором производительностью 5,6 м3/ч (при условиях всасывания). Компрессор сжимает диоксид углерода от 20 до 70 кгс/см2 (давление абсолютное). Начальная температура -15°С. К. п. д. компрессора принять равным 0,65. Задачу решить как аналитическим путём, так и диаграммы T – S для углерода (рис. XXVII).

К этой задаче смотри пример 2.14.

1) Работа, затрачиваемая на адиабатическое сжатие 1 кг СО2: а) Аналитически:

Затрату работы на сжатие 1 кг углекислого газа находим по формуле (2.12): показатель адиабаты k находим по таблице V: k = 1,3.

k−1

1,3−1

1,3

8310

Дж

1,3

R T

−1

258

−1

= 70782

ад 1

k −1

1,3 −1

кг

б) Графически с использованием формулы (2.13):

На T – S диаграмме сначала находим точку с координатами -15 °C; 20 кгс/см2. Энтальпия в этой точке приблизительно равна i1 = 157,7 ккал/кг. В адиабатном процессе изменения энтропии не происходит, поэтому от этой точки поднимаемся вверх по линии S = const до пересечения с изобарой

70 кгс/см2. Здесь энтальпия i1 = 169 ккал/кг.

Lад 2 = i2 – i1 = 169,5 – 158,2 = 11,3 ккал/кг = 11,3·4190 = 47347 Дж/кг.

Значения, полученные двумя способами, очень сильно различаются. Это обусловлено тем, что при низких температурах и высоких давлениях газ уже нельзя считать идеальным, а в этом случае P·V ≠ R·T и формулу (2.12) использовать нельзя. Работа в этом случае рассчитывается по формуле (2.13) с использованием диаграмм. [Об этом см. Гельперин Н.И. Основные процессы и аппараты химической технологии М.: Химия 1981, первый том, стр. 137.]

2) Плотность при условиях всасывания находим по формуле (1.5):

ρсм	= ρо	То Рабс	=1,98	273 20 9,81 104	= 40,58	кг	.
		Р Т		1,013 105 258
						м3
		о

3)Массовый расход находим по формуле (1.18): G = Q·ρ = 5,6·40,58 = 227 кг/ч.

4)Затрачиваемую мощность найдём по формуле (2.15):

=	G Lад			=	227 47347	= 4,6 кВт .
	3600	1000	η		3600 1000 0,65

vk.com/club152685050 | vk.com/id446425943

№21. Определить объёмный к. п. д. компрессора предыдущей задачи, если вредное пространство составляет 6% от объёма, описываемого поршнем, а показатель политропы расширения m = 1,2.

Объёмный к. п. д. находим по формуле (2.17):

1,2

= 1− ε

−1

= 1− 0,06

−1 = 0,89

Р1

№22. Определить производительность и расходуемую мощность для одноступенчатого поршневого компрессора по следующим данным: диаметр поршня 250 мм, ход поршня 275 мм, объём вредного пространства 5,4% от объёма, описываемого поршнем, частота вращения 300 об/мин. Компрессор сжимает атмосферный воздух до Рабс = = 4 кгс/см2. Показатель политропы расширения на 10% меньше показателя адиабаты. Начальная температура воздуха 25 °С. Общий к. п. д. равен 0,72.

1) Плотность при условиях всасывания находим по формуле (1.5):

ρсм	= ρо	То Рабс	=1,293	273	=1,1845	кг	.
		Р Т
			298			м3
		о

2) Находим объёмный к. п. д. по формуле (2.17):

по таблице V показатель адиабаты для воздуха k = 1,4; показатель политропы по условию на 10% меньше:

m = 0,9·1,4 = 1,26;

4 9,81 104

1,26

=1−ε

−1

=1− 0,054

−1

= 0,896.

1,013 105

3)Коэффициент подачи примем равным λ = 0,9·λо = 0,8064

4)Производительность находим по формуле (2.16):

Q = λ	F s n	= λ π d2 s n = 0,8064	0,785 0,252	0,275 300	= 0,05417	м3	= 0,05417 60 = 3,25	м3	.

60		4 60	60			с		мин

5) Массовый расход находим по формуле (1.18):

G = Q·ρ = 0,05417·1,1845 = 0,06416 кг/с = 0,6416·3600 = 231 кг/ч.

6) Затрату работы на сжатие 1 кг воздуха находим по формуле (2.13) с использованием T – S диаграммы:

vk.com/club152685050 | vk.com/id446425943

На T – S диаграмме сначала находим точку с координатами 25 °C; 1 кгс/см2. Энтальпия в этой точке приблизительно равна

i1 = 121,8 ккал/кг. В адиабатном процессе изменения энтропии не происходит, поэтому от этой точки поднимаемся вверх по линии S = const до пересечения с изобарой 4 кгс/см2. Здесь энтальпия i2 = 156,6 ккал/кг.

Lад = i2 – i1 = 156,6 – 121,8 = 34,8 ккал/кг = 4190·34,8 = 145952 Дж/кг.

7) Затрачиваемую мощность найдём по формуле (2.15):

=	G Lад			=	231 145952		=13 кВт.
	3600	1000	η		3600	1000 0,72

№23. Как изменятся производительность и потребляемая мощность компрессора предыдущей задачи, если дать ему воздуходувкой наддув до Ризб = 0,4 кгс/см2. Конечное давление (абсолютное) 4 кгс/см2.

1) Плотность при условиях всасывания находим по формуле (1.5):

ρ		= ρ		То Рабс	=1,293	273 (1,013 105 + 0,4 9,81 104 )	=1,643
	см		о	Р Т
						1,013 105 298
				о

2) Находим объёмный к. п. д. по формуле (2.17):

по таблице V показатель адиабаты для воздуха k = 1,4; показатель политропы по условию на 10% меньше:

m = 0,9·1,4 = 1,26;

кг м3 .

4 9,81 104

1,26

=1−ε

−1

=1− 0,054

−1

= 0,932.

105 + 0,4 9,81 104

1,013

3)Коэффициент подачи примем равным λ = 0,92·λо = 0,8574.

4)Производительность находим по формуле (2.16):

Q = λ	F s n	= λ π d2 s n = 0,8574	0,785 0,252	0,275 300	= 0,05767	м3	= 0,05767 60 = 3,46	м3	.

60		4 60	60			с		мин

5) Массовый расход находим по формуле (1.18):

vk.com/club152685050 | vk.com/id446425943

G = Q·ρ = 0,05767·1,643 = 0,09475 кг/с = 0,9475·3600 = 341 кг/ч.

6) Затрату работы на сжатие 1 кг воздуха находим по формуле (2.12):

k−1

1,4−1

1,4

8310

4 98100

1,4

Дж

R T

−1

298

−1

=101897

k −1

−1

1,013 105 + 0,4 9,81 104

ад

1,4

кг

7) Затрачиваемую мощность найдём по формуле (2.15):

=	G Lад			=	341 101897	=13,4 кВт .
	3600	1000	η		3600 1000 0,72

№24. При каком давлении нагнетания объёмный к. п. д. одноступенчатого поршневого компрессора, сжимающего этилен, упадёт до 0,2? Давление всасывания 1 кгс/см2. Расширение газа из вредного пространства считать адиабатическим. Объём вредного пространства составляет 7% от объёма, описываемого поршнем.

Так как в нашем случае расширение этилена из вредного пространства происходит по адиабате, формула (2.17) принимает вид:

Р2

= 1 − ε

− 1

- вместо показателя политропы m исполь-

Р1

зуется показатель адиабаты k. По таблице V показатель адиабаты для этилена k = 1,2.

Отсюда выражаем давление нагнетания Р2:

−1

+1;

−ε

λo

−1

0,2 −1

1,2

2084082

кгс

P2 = P1

=1,013 10

= 2084082 Па =

= 20,6

−

εo

9,81 10

см

- 0,07

№25. Исходя из условия, что компрессорное смазочное масло допускает без заметного ухудшения смазки температуру в цилиндре не выше 160°С, определить предельное значение давления нагнетания в одноступенчатом поршневом компрессоре: а) для воздуха, б) для этана. Давление всасывания 1 кгс/см2. Начальная температура 25 °С. Процесс сжатия считать адиабатическим.

Давление нагнетания выразим из формулы (2.14):

vk.com/club152685050 | vk.com/id446425943

k−1

k −1

;

= Р

а) Для воздуха по таблице V находим показатель адиабаты: k = 1,4;

k−1

1,4−1

= Р1

=1,013 10

433

= 374593 Па =

374593

= 3,697

кгс

Р2

1,4

298

9,81 104

см2

б) Для этана по таблице V находим показатель адиабаты: k = 1,2;

k−1

1,2−1

433

923206

кгс

= Р1

=1,013 10

= 923206 Па =

= 9,41

Р2

1,2

;

298

9,81 104

см2

№26. По данным примера 2.17 определить для одноступенчатого и двухступенчатого компрессоров теоретическую затрату работы по формулам (2.13) и (2.19).

а) Для одноступенчатого

На T – S диаграмме для воздуха сначала находим точку с координатами 20 °C; 1 кгс/см2. Энтальпия в этой точке приблизительно равна i1 =

= 120,6 ккал/кг. В адиабатном процессе изменения энтропии не происходит, поэтому от этой точки поднимаемся вверх по линии S = const до пересечения с изобарой 9 кгс/см2. Здесь энтальпия i2 = 182,9 ккал/кг. По формуле (2.13):

Lад = i2 – i1 = 182,9 – 120,6 = 62,3 ккал/кг = 4190·62,3 = 261037 Дж/кг.

б) Для двухступенчатого В каждой ступени происходит сжатие воздуха в три раза:

Р1 = Р2 = 3 , т.е. Р1 = 3 кгс/см2, а Р2 = 9 кгс/см2.

Р0 Р1

На T – S диаграмме для воздуха сначала находим точку с координатами 20°С; 1 кгс/см2. Поднимаемся вверх по линии S = const до пересечения с изобарой 3 кгс/см2. Замеряем энтальпии в этих точках, их разность – это ∆i1. Дальше по изобаре Р = 3 кгс/см2 спускаемся до температуры 20°С. Отсюда опять поднимаемся по линии S = const до пересечения с изобарой 9 кгс/см2. Замеряем энтальпии, их разность – это ∆i2. По формуле (2.19):

Lад = ∆i1 + ∆i2.

На всех T – S диаграммах, которые у меня есть, не хватает шкалы температур, чтобы все это найти, так что пришлось обойтись без цифр.

vk.com/club152685050 | vk.com/id446425943

№27. Определить требуемое число ступеней поршневого компрессора, который должен сжимать азот от 1 до 100 кгс/см2 (давление абсолютное), если допускаемая температура в конце сжатия не должна превышать 140 °С. Процесс сжатия считать адиабатическим. Начальная температура азота 20 °С.

1) Чтобы найти число ступеней по формуле (2.21) нужно сначала						знать
Рконв одной ступени
степень сжатия в одной ступени x =		. Она связана с температурой
степень сжатия в одной ступени x =	в одной ступени	. Она связана с температурой
Рнач
							k−1
					Рв одной ступени		k
в конце сжатия в каждой ступени формулой (2.14): T			= Т		кон
в конце сжатия в каждой ступени формулой (2.14): T			= Т	нач
		кон		нач	в одной ступени
					Рнач

[см. пример 2.17]. Температура

в конце сжатия у нас есть, выражаем

Рв одной ступени

кон

Рв одной ступени

нач

по таблице V находим, что показатель адиабаты для азота равен: k = 1,4;

Рв одной ступени

1,4−1

k−1 Т

413

x =

кон

1,4

= 3,3249.

Рв одной ступени

293

нач

2) Теперь по формуле (2.21) находим число ступеней:

xn =

Рв конце сжатия

;

Рначальное

n = log3,32100 = 3,8 .

То есть для выполнения задания нужно 4 ступени сжатия.

№28. Определить теоретическую затрату работы на сжатие водорода от 1,5 до 17 кгс/см2 (давление абсолютное) при одноступенчатом и двухступенчатом сжатии начальная температура водорода 20°С.

а) При одноступенчатом – по формуле (2.12):

по таблице V находим показатель адиабаты водорода: k = 1,407;

k−1

1,407−1

1,407

8310

1,407

Дж

3 кДж

ад

−1

293

−1

= 4285744

≈ 4,28 10

R T

k −1

1,407 −1

кг

1,5

б) При двухступенчатом – по формуле (2.18):

								k−1									1,407−1
					k	Р	кон	k n					8310		1,407	17		1,407 2					Дж				3	кДж
	=			1			кон		−		=								−		=			≈
ад	=	n	R	1					−	1	=	2		293					−	1	=	3540944		≈	3,54	10			.
L		n	R	T			1			1		2		293						1		3540944			3,54	10			.
					k −1		1						2		1,407 -1								кг					кг
					k −1	Р							2		1,407 -1	1,5							кг					кг

vk.com/club152685050 | vk.com/id446425943

№29. Компрессор при испытании нагнетал атмосферный воздух в баллон объёмом 42,4 дм3. За 10,5 минут давление в баллоне повысилось от 0 до 52 кгс/см2 (давление избыточное), а температура воздуха в баллоне поднялась от 17 до 37 °С. Определить производительность компрессора в м3/ч (при нормальных условиях).

1) Объёмный расход воздуха:

V		=	42,410−3	= 6,7310−5	м3
Q =						.
	τ		10,5 60		с

2) Плотность при конечных условиях сжатия ищем по формуле (1.5):

ρ =	М	То Р	=	29	273 (1,013 105 + 52 9,81 104 )	= 58,55	кг
								.
	22,4	Ро Т		22,4	1,013 105 310		м3

3)Массовый расход воздуха при конечных условиях сжатия: G = Q·ρ = 6,73·10-5·58,55 = 3,94·10-3 кг/с.

4)Плотность воздуха при нормальных условиях находим по таблице V: ρо = = 1,293 кг/м3.

5)Производительность компрессора при нормальных условиях:

	G	=	3,94 10−3	= 3,047 10−3	м3	= 10,9	м3
Qo =								.
	ρo
			1,293		с		ч

№30. Определить потребляемую мощность и расход воды на холодильники поршневого компрессора, который сжимает 625 м3/ч (при нормальных условиях) этилена от давления (абсолютного) 9,81·104 до 176,6·104 Па. К. п. д. компрессора 0,75. Охлаждающая вода нагревается в холодильниках на 13 °С. Начальная температура газа 20 °С.

К этой задаче смотри пример 2.18. Массовый расход этилена:

ρо = 1,26 кг/м3 (таблица V);

G = Qо·ρо = 625·1,26 = 787,5 кг/ч.

По таблице V показатель адиабаты этилена k = 1,2.

а) Рассмотрим двухступенчатое сжатие (одноступенчатого здесь быть не может, раз уж есть холодильники :).

1) Находим теоретическую величину работы по формуле (2.18):

vk.com/club152685050 | vk.com/id446425943

						k−1						1,2−1

					k n						176,6 104	1,2 2
			k	Ркон	k n			8310		1,2	176,6 104	1,2 2
L	ад	= n RT					−1 = 2		293
L		= n RT					−1 = 2		293		4
		1									4
			k −1	Р1				28		1,2 -1	9,81 10
			k −1	Р1				28		1,2 -1	9,81 10

−1 = 284208 Дж .

кг

2) Мощность потребляемую компрессором находим по формуле (2.15):

G Lад

787,5 284208

= 82,9 кВт .

1000 η

3600 1000 0,75

3600

3) Расход охлаждающей воды находим из уравнения теплового баланса:

Gэт·Lад = Gв·св·(t2 – t1);

Gв =

Gэт Lад

787,5 284208

= 1,14137

кг

=1,14137 3600 = 4109

кг

;

−t )

3600 4190 13

Qв =

Gв

4109

≈ 4,11

м3

ρв

1000

б) Рассмотрим трёхступенчатое сжатие.

1) Находим теоретическую величину работы по формуле (2.18):

k−1

1,2−1

кон

k n

8310

1,2

176,6 104

1,2 3

Дж

Lад = n R T1

−1 = 3

293

−1

= 272658

k −1

Р1

1,2 -1

9,81 10

кг

2) Мощность потребляемую компрессором находим по формуле (2.15):

G Lад

787,5 272658

= 79,5 кВт.

3600 1000 η

3600 1000 0,75

3) Расход охлаждающей воды находим из уравнения теплового баланса: Gэт·Lад = Gв·св·(t2 – t1);

Gв =

Gэт Lад

787,5 272658

=1,09498

кг

=1,09498 3600 = 3942

кг

;

−t )

3600 4190 13

Qв =

Gв

3942

≈ 3,94

м3

ρв

1000

vk.com/club152685050 | vk.com/id446425943

МИНОБРНАУКИ РОССИИ

федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный технологический институт (технический университет)»

(СПбГТИ (ТУ))

Кафедра оптимизации химической и биотехнологической аппаратуры

И. В. Доманский, В. А. Некрасов

ОСНОВЫ ГИДРОМЕХАНИКИ

УЧЕБНОЕ ПОСОБИЕ

Санкт-Петербург

2015

vk.com/club152685050 | vk.com/id446425943

УДК 532.5

Доманский, И.В. Основы гидромеханики: учебное пособие /И.В. Доманский, В. А. Некрасов. – СПб.: СПбГТИ (ТУ), 2015. – 121 с.

Учебное пособие содержит краткий курс лекций по дисциплинам «Основы гидромеханики» и «Механика жидкости и газа».

Рассмотрены основные законы и уравнения гидромеханики, охватывающие разделы свойств жидкостей, гидростатики, кинематики и динамики жидкостей, гидродинамического подобия и особых случаев течения.

Изложены основные вопросы, направленные на приобретение студентами теоретических знаний и практических навыков по их применению в технических приложениях.

Учебное пособие предназначено для бакалавров 2 и 3 курсов дневной и заочной формы подготовки по направлениям: 08.03.01 Строительство (270800.62 Профиль подготовки № 8 Механическое оборудование и технологические комплексы предприятий строительных материалов, изделий и конструкций); 15.03.02 Технологические машины и оборудование (151000.62 Профиль подготовки № 13 Технологическое оборудование химических и нефтехимических производств), а также бакалавров 3 курса по направлению: 220000 – Автоматика и управление (220400.62 – Управление в технических системах; 220700.62 – Автоматизация технологических процессов и производств) и другим, связанным с теорией жидкости.

Учебное пособие способствует формированию ОК: 1, 9; ПК: 4, 17, 18

Ил. 79, табл. 2, библиогр. 6 назв.

Рецензенты:

1 – НИУ ИТМО, институт холода и биотехнологий, зав. каф. ПиАПП, д-р техн.наук, проф. Г.В. Алексеев;

2 – Т.М. Лебедева, канд. техн. наук, доц. кафедры ОРПП, СПбГТИ(ТУ)

Утверждено на заседании учебно-методической комиссии механического факультета 20 января 2015 г.

Рекомендовано к изданию РИСО СПбГТИ(ТУ)

Доманский И. В., Некрасов, В. А.

vk.com/club152685050 \| vk.com/id446425943
СОДЕРЖАНИЕ
Предисловие…………………………….……………………………..	6
Введение……………………………………………………………….	7
1 Основные понятия и определения...…………………………………	9
Контрольные вопросы………………………………………………...	12
2 Элементы кинематики жидкости………………………...……..……	13
2.1 Основные понятия…………………………………………………	13
2.2 Уравнение неразрывности…………………………………...	16
2.3 Скорость деформации………………………………………	18
Контрольные вопросы…………………………………….……...	22
3 Основные уравнения динамики несжимаемой жидкости.….…..…..	23

3.1Силы в жидкости.....……………..…………................................... 23

3.2Уравнение движения в напряжениях ……………..…………... 27

3.3Уравнение движения вязкой несжимаемой жидкости

(уравнение Навье-Стокса)………………………………….....…. 28

3.4Уравнение энергии ……………………………………………..... 29

Контрольные вопросы..…………………………………………...		31
4 Гидростатика ……………………………….........................................		31
4.1 Дифференциальные уравнения равновесия жидкости (уравне-
ния Эйлера)………………………………………...………………		31

4.2Равновесие жидкости в гравитационном поле. Основное уравнение гидростатики………………………………………….. 33

4.3 Сообщающиеся сосуды ……………………………..…...………		34
4.4	Равновесие жидкости в центробежном поле…….….………..	36
4.5	Сила давления на плоскую поверхность тела…………………	37

4.6Сила давления на цилиндрическую поверхность тела…..…….. 38

4.7Закон Архимеда……………….…………….……………………. 39

Контрольные вопросы…..………………………………………...		40
5 Динамика идеальной жидкости.………….………………………..		40
5.1 Уравнение движения идеальной жидкости
(уравнение Эйлера)……………..…………………………………		40

5.2Уравнение Бернулли для плоского установившегося течения. 41

5.3Плоские потенциальные течения……………………………..…. 43

Контрольные вопросы…………..………………………………... 47

vk.com/club152685050 | vk.com/id446425943

6 Общие закономерности динамики вязкой жидкости………………. 48

6.1Два режима течения…………………….........…………………. 48

6.2Уравнение турбулентного течения несжимаемой жидкости

	(уравнение Рейнольдса)…………………………...…….………	49
6.3	О моделировании в гидромеханике…………………….………	50
6.4	Решение задач гидродинамики методом теории подобия..…..	51
6.5	Ламинарное безнапорное течение Куэтта…………………..…	54

6.6Ламинарное равномерное течение в плоском канале………..... 54

6.7Ламинарное течение в плоском клиновидном зазоре…..……. 56

6.8Ламинарное течение жидкости в зазоре подшипника

скольжения………………………………………………………... 58 6.9 Ламинарное течение в круглой трубе……………………..…….. 60 6.10 Турбулентное безнапорное течение Куэтта……..…………… 62

6.11Сопротивление гидравлически гладких труб при турбулентном течении жидкости………………….…….. 65

6.12Сопротивление гидравлически шероховатых труб при турбулентном режиме течения жидкости……………….. 67

6.13 Ламинарное обтекание шара (задача Стокса)..………………		68
6.14 Уравнения пограничного слоя……..……………………..……		71

6.15Интегральное соотношение пограничного слоя……………... 72

6.16Ламинарный пограничный слой на полубесконечной пластине…………………………...……………………….…….. 74

6.17Турбулентный пограничный слой на полубесконечной

пластине………...…………………………………………………. 75 6.18 Струйное течение………………………..……………………... 76 Контрольные вопросы………..………..………………………... 78 7 Одномерные течения вязкой жидкости………..…………………. 79

7.1Уравнение Бернулли для потока вязкой жидкости……….…. 79

7.2Уравнение Бернулли для сети с насосом……….……………. 81

7.3Гидравлические потери по длине………………………..…….. 82

7.4Гидравлические потери на местных сопротивлениях…………. 82

7.5Приборы для измерения скоростей и расходов..….…………. 86

7.6Истечение жидкости………………………….…………………... 89

7.7Поле скоростей и давлений в циклонном устройстве……….. 93

vk.com/club152685050 | vk.com/id446425943

7.8 Вторичные токи в реальной жидкости….……….…………….. 94

7.9 Гидравлический удар в трубах…………..……………………… 96

7.10Высота всасывания центробежного насоса…..………………. 100

7.11Высота всасывания поршневого насоса…..…….……….……. 101

7.12Трубопровод с путевым расходом………………………….…. 105

Контрольные вопросы…………..………………….…………...	108
8 Сжимаемые жидкости……………………………………………..….	109

8.1Одномерное движение идеального газа……………………….… 110

Контрольные вопросы.…………..………………………………... 112

Литература……………………………………………………………...		114
Приложение А Векторы и операции над ними…………..……….…		115
Приложение В Компоненты векторов и основные уравнения в кри-
волинейных координатах ………………………….…….…...		118

vk.com/club152685050 | vk.com/id446425943

Предисловие

Основой для написания настоящего пособия послужило учебное пособие И.В. Доманского «Гидравлика и гидравлические машины» 1989 года издания, которое подверглось значительной переработке. С целью большей наглядности излагаемого материала увеличено количество иллюстраций. Ряд параграфов значительно расширен. В шестом разделе приведен пример точного решения для подшипника скольжения. Уточнен ряд отдельных результатов. Добавлен один раздел и два приложения.

Пособие предназначено для бакалавров 2 и 3 курсов дневной и заочной формы подготовки по направлениям: 08.03.01 Строительство (270800.62 Профиль подготовки № 8 Механическое оборудование и технологические комплексы предприятий строительных материалов, изделий и конструкций); 15.03.02 Технологические машины и оборудование (151000.62 Профиль подготовки № 13 Технологическое оборудование химических и нефтехимических производств), а также бакалавров 3 курса по направлению: 220000 – Автоматика и управление (220400.62 – Управление в технических системах; 220700.62 – Автоматизация технологических процессов и производств).

В пособии в конспективной форме изложены основы теории и технических приложений механики жидкости и газа. Пособие написано с учетом противоречивых условий. С одной стороны в соответствии с ФГОС ВПО область профессиональной подготовки бакалавров включает в себя решение достаточно широкого круга задач, связанных с механикой жидкости и газа. С другой – крайне ограниченное время, отводимое на данную дисциплину в учебных планах. В связи с этим часть материалов предназначена непосредственно для привития бакалаврам умений и навыков, необходимых для профессиональной деятельности. Другая часть материалов может рассматриваться как факультативная или рекомендуемая для самостоятельного изучения, или для подготовки магистров и аспирантов.

vk.com/club152685050 | vk.com/id446425943

Введение

Механика жидкостей и газов, или гидромеханика, так же как и другие области механики, разделяется на статику, кинематику и динамику. Часть гидромеханики, изучающая условия равновесия жидкостей и газов, называется гидростатикой. Кинематика жидкостей и газов изучает их движение во времени, не интересуясь причинами, вызывающими это движение. Предметом изучения гидродинамики являются движения жидкостей и газов с учетом действующих сил.

Гидромеханика в качестве основного метода исследований использует строгий математический анализ. Вначале независимо, а затем параллельно гидромеханике развивалась гидравлика – прикладная инженерная наука о равновесии и движении жидкостей, основанная преимущественно на экспериментальных данных и разрабатывающая приближенные методы расчета течений жидкости в трубах, каналах и реках.

Жидкости и газы обладают двумя основными свойствами: сплошностью и легкой подвижностью, или текучестью.

Известно, что все тела состоят из движущихся и взаимодействующих между собой молекул. Механика не занимается изучением движения отдельных молекул, а исходит из допущения, что все пространство непрерывно (сплошным образом) заполнено веществом.

Условие сплошности для жидкостей и газов выполняется, если характерные линейные размеры области течения (диаметр трубы, размах крыла и др.) велики по сравнению с параметрами, характеризующими движение молекул. Для газов таким параметром является длина свободного пробега молекул. Для жидкостей – амплитуда колебаний молекул.

Легкая подвижность, или текучесть, позволяет ввести понятие вязкости как свойства жидкостей и газов оказывать сопротивление при их перемещении.

Гидромеханика изучает законы движения так называемых ньютоновских жидкостей, для которых напряжения, вызываемые наличием вязкости, выражаются линейно через скорости деформаций.

Для неныотоновских жидкостей эта зависимость значительно сложнее. Законы движения неньютоновских жидкостей изучает реология.

В гидромеханике иногда пользуются моделью идеальной жидкости, для которой вязкость принимается равной нулю, т. е. она обладает бесконечно большой текучестью. Такая модель применима в тех случаях, когда силами вязкости можно пренебречь по сравнению с другими действующими силами.

Гидромеханика прошла большой и сложный путь развития. Ее предыстория уходит в древние времена.

Так, например, рождение научной дисциплины гидравлики, точнее – гидростатики, обычно связывают с именем Архимеда (277 – 212 гг. до н. э.).

Особое развитие гидравлика получила в средние века благодаря трудам Леонардо да Винчи (1452 – 1519 г.г.), Г. Галилея (1564 – 1642 г.г.), Э. Торри-

челли (1608 – 1647 г.г.), Б. Паскаля (1623 – 1662 г.г.), И. Ньютона (1642 – 1726 г.г.).

vk.com/club152685050 | vk.com/id446425943

Начало гидромеханике как науке было положено в XVII столетии трудами академиков Российской Академии Наук Леонарда Эйлера (1707 – 1783 г.г.) и Даниила Бернулли (1700 – 1782 г.г.).

Дальнейший этап в истории развития гидромеханики (конец XVIII и начало XIX веков) характеризуется математической разработкой гидродинамики идеальной жидкости. В этот период вышли труды французских математиков Лагранжа (1736 – 1813 г.г.) и Коши (1789 – 1857 г.г.).

Основы теории движения вязкой жидкости были заложены французским ученым Навье (1785 – 1836 г.г.) и английским физиком и математиком Стоксом

(1819 – 1903 г.г.).

Наряду с теоретическими работами в середине и конце XVIII в. развивалось техническое направление механики жидкости. В результате усилий многих ученых и инженеров – А. Пито (1695 – 1771 г.г.), А. Шези (1718 – 1798 г.г.), Ж. Борда (1733 – 1799 г.г.), Г. Дарси (1803 – 1858 г.г.), Д. Вентури (1746 – 1822 г.г.) и др. – были получены эмпирические формулы для определения скорости движения, потерь напора жидкости по длине и на местных сопротивлениях.

Особая роль в формировании механики жидкости принадлежит английскому ученому О. Рейнольдсу (1842—1912 г.г.). Им определены условия перехода ламинарного движения в турбулентное, установлены принципы гидродинамического подобия.

Из работ в области механики жидкости и газа начала XX в. следует выделить фундаментальные работы Л. Прандтля (1875 – 1953 г.г.), создавшего основы современной теории пограничного слоя, а также работы Т. Кармана (1881 – 1963 г.г.), разработавшего приближенный метод расчета характеристик пограничного слоя.

Широко известны работы русских ученых, таких как Д.И. Менделеев

(1834 – 1907 г.г.), И.С. Громеко (1851 – 1889 г.г), Н.П. Петров (1836 – 1920 г.г.),

Н.Е. Жуковский (1847 – 1921 г.г.), С.А. Чаплыгин (1869 – 1942 г.г.), А.Н. Крылов (1863 – 1945 г.г.), Н.Н. Павловский (1884 – 1937 г.г.) и многие другие.

Современный этап развития гидромеханики характеризуется появлением ее новых разделов: физико-химической и электромагнитной гидродинамики, газодинамики сверхзвуковых и гиперзвуковых скоростей.

vk.com/club152685050 | vk.com/id446425943

1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

При проведении теоретического анализа поведения жидкостей и газов в гидромеханике пользуются понятием «сплошная среда» – материальное тело, непрерывно распределенное в пространстве. Введение этого понятия позволяет проводить дифференцирование, предопределяет плавное изменение параметров в любой точке пространства. Правомерность этой гипотезы доказана согласием теории и эксперимента в многочисленных задачах гидромеханики.

Плотность среды в произвольной точке пространства определяется соотношением

ρ lim	m	,	(1.1)
V 0	V

где m – масса жидкости, находящейся в объеме V. Размерность [ ] = кг/м3. Плотность среды зависит от температуры Т и давления р. Связь

= (р, Т)

(1.2)

называется уравнением состояния. Для газов – это уравнение МенделееваКлапейрона

pV	mRMT	p	RT ,	(1.3)
	M

где m – масса газа;

RM – универсальная газовая постоянная (RM = 8314 Дж/(кмоль К);

R = RM/М – удельная газовая постоянная (для воздуха R = 287 Дж/(кг К); Т – абсолютная температура, К; М – молярная масса газа, кг/кмоль.

Вязкость жидкости характеризует способность ее сопротивляться сдвиговым усилиям.

z
z	u0
		F

Рисунок 1.1 – Схема течения в канале Куэтта

Если между двух параллельных пластин (рис. 1.1) поместить жидкость, то для приведения верхней пластины в движение со скоростью u0 необходимо приложить силу F, причем при ламинарном режиме течения

vk.com/club152685050 \| vk.com/id446425943
F S	u0	,	(1.4)

где S – площадь пластин, м2;

– расстояние между ними, м;

– коэффициент пропорциональности, называемый коэффициентом дина-

мической вязкости.
Размерность в системах СИ и СГС, соответственно:
F	H м	Па с	кг	; [ ]	г		Пуаз .
	м2 м с		м с		см
S u						с

В условиях ламинарного течения между пластинами установится линейный профиль скоростей (см. рис. 1.1), тогда

u0 du .dz

Кроме того, F/S = , где – касательное напряжение. Тогда соотношению (1.1) можно придать вид

du	.	(1.5)

dz

Уравнение (1.5) выражает закон внутреннего трения Ньютона при одномерном течении.

Наряду с коэффициентом динамической вязкости в гидродинамике ис-

пользуется и коэффициент кинематической вязкости:

	/ .		(1.6)
Размерность в СИ: [ ] = м2 /c, в СГС: [ ] = см2 /c = 1 стокс (Ст);
1 Ст = 10-4 м2/с.
Вязкость воды при 20 °С = 1 сСт = 10-2 Ст = 10-6 м2/с; = 10-3 Па с.

		б

а – для жидкости; б – для газа

Рисунок 1.2 – Характер зависимости динами-

ческой вязкости от температуры T

Вязкость жидкостей и газов существенно зависит от температуры, причем с ростом температуры вязкость газов возрастает, а жидкостей – падает (рис.

1.2).

vk.com/club152685050 | vk.com/id446425943

Жидкости, которые при постоянной температуре характеризуются уравнением (1.5) с постоянным коэффициентом , называются ньютоновскими (вода, керосин, спирт и др.). Реологическая характеристика их (зависимость τ = τ(du/dz) имеет вид прямой, проходящей через начало координат (рис. 1.3).

Жидкости с характеристиками любого другого вида называются ненью-

тоновскими. К бингамовским жидкостям относятся глинистые и цементные растворы, пасты, пена, масляные краски и пр. К псевдопластическим – суспензии из ассиметричных частиц, растворы полимеров, целлюлоза и пр. К дила-

тантным – клейстер, крахмал. Дисциплина, изучающая механику неньютоновских жидкостей, называется реологией.

		2
		2
			3



	1
0	1
0
			4

du/dz

1 – ньютоновской; 2 – бингамовской;

3 – псевдопластической; 4 – дилатантной

Рисунок 1.3 – Вид реологических характеристик

жидкостей

В теоретической гидромеханике для упрощенного решения задач введено понятие идеальной жидкости. Это сплошная среда, у которой

= = 0; 0.

Сжимаемость жидкости характеризуется коэффициентом объемного сжатия (коэффициентом сжимаемости) р (Па-1)

	1	1	1	,
p
	p	p E0

где = 1/ – удельный объем, м3/кг; Е0 – объемный модуль упругости, Па. Для характеристики сжимаемости движущегося газа используется поня-

тие скорости звука.

Скорость звука с – скорость распространения малых возмущений давления в сплошной среде, обусловленных изменением во времени скорости движения. В однородной среде

	p		E0
c		kRT		,

где k – показатель коэффициент адиабаты.

При решении конкретных задач, несмотря на значительную сжимаемость

vk.com/club152685050 | vk.com/id446425943

газов по сравнению с жидкостями, при скоростях в средах υ < 0,1с сжимаемостью можно пренебречь. Поэтому понятие ―несжимаемая жидкость‖ нашло широкое применение.

Поверхностное натяжение , Н/м. Это свойство проявляется на границе раздела фаз и оказывает влияние на равновесие или движение жидкости в тех случаях, когда изменяется форма или величина поверхности раздела фаз.

По физическому смыслу это свободная потенциальная энергия единицы по-

верхности раздела, обусловленная действием сил притяжения на расположенные в непосредственной близости от нее молекулы.

Поверхностное натяжение приходится учитывать при работе с жидкостными приборами для измерения давления, образовании капель и в других случаях, когда прочие силы малы.

Испарение. Это свойство капельной жидкости изменять свое агрегатное состояние, в частности превращаться в пар.

Если на поверхности раздела фаз жидкость-пар парциальное давление пара рп меньше давлением насыщенных паров рн. п, то происходит испарение жидкости, если больше – то конденсация пара. Снижение локального давления в движущейся жидкости ниже давления насыщенного пара нередко сопровождается образованием пара в объеме жидкости (холодное вскипание жидкости), т.е. потерей ее сплошности. Если при дальнейшем движении происходит рост давления, то ранее образовавшийся пар конденсируется и полости, ранее занятые паром, мгновенно заполняются жидкостью. Это явление в технической гидродинамике называется кавитацией (от латинского "кавитас" – полость).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 В чем заключается гипотеза сплошности жидкости? 2 Каковы отличия жидкости от твердых тел и газов? 3 Что такое плотность жидкости, от чего она зависит?

4 Что такое динамическая и кинематическая вязкость? Как они определяются? 5 Каков характер зависимости вязкости газов и жидкостей от температуры?

6 В каких условиях не стоит пренебрегать сжимаемостью жидкости в гидравлике?

7 Что следует понимать под давлением насыщенных паров?

8 Каковы особенности реологических характеристик неньютоновских жидкостей.

9Реологическая характеристика жидкости. Классификация жидкостей.

10В чем состоит физический смысл объемного модуля упругости?

11Какие причины вызывают кавитацию?

12Что такое "холодное" кипение?

13Какова физическая природа явления поверхностного натяжения?

vk.com/club152685050 \| vk.com/id446425943
2 ЭЛЕМЕНТЫ КИНЕМАТИКИ ЖИДКОСТИ
2.1 Основные понятия
Скорость жидкости может быть задана двумя способами. Первый из них
(метод Лагранжа), наиболее естественный, предполагает известными траекто-
рии движения каждой жидкостной частицы, имеющей в начальный момент
времени координаты		r0 или		(а, b, с);			r r	r0 ,t или х = х(а, b, с, t);
у = у(а, b, с, t); z = z(a, b, с, t). Переменные r0								или а, b, с называются пере-
менными Лагранжа. В этом случае мгновенную скорость можно вычислить
так:
u	x	dx ; u	y	dy ;	u	z	dz ;	u dr .
	x	dt	y	dt		z	dt	dt
		dt		dt			dt	dt
Отметим, что этот метод описания движения жидкости не получил широко-
го применения из-за сложности получаемых уравнений движения.
Второй метод (метод Эйлера) заключается в непосредственном описании
поля скоростей в пространстве и времени: u u r , t или ux = ux(x, y, z, t);
uy = uy(x, y, z, t) и uz = uz(x, у, z, t).
Этот метод получил преимущественное применение.
Движение называется установившимся или стационарным , если
скорость в каждой точке пространства не изменяется во времени (например, ис-
течение жидкости из отверстия в днище сосуда при постоянном уровне жидко-
сти). Если же скорость изменяется во времени, то движение называется неус-
тановившимся или нестационарным.
Линия тока – это линия, в каждой точке которой в данный
момент времени вектор скорости u						направлен по касательной (рис.
2.1).
		u(r, t)			2
z					2
z						3
						3
r								u(r + r, t + t)
		r + r						u(r + r, t + t)
		r + r			1
					1
x		y
1 и 2 – линии тока в моменты времени t и t + t;
		3 – траектория
Рисунок 2.1 – Линии тока и траектория
Из определения	следует,		что u dr , т. е.					их векторное произведение
u dr 0, или, т. к. u uxi uy j uz k ,					а dr idx jdy kdz , то
uy dz uz dy i uz dx uxdz j uxdy uy dx k 0
				13

vk.com/club152685050 | vk.com/id446425943

или

dx	dy	dz	.	.	(2.1)

ux	uy	uz

Уравнение (2.1) – это дифференциальное уравнение линии тока.

Траектория – это линия, по которой материальная точка пер е- мещается в пространстве во времени (см. рис. 2.1). За время dt точка пройдет путь dr udt . В проекции на оси координат dx=uxdt; dy=uydt; dz=uzdt или

dt	dx	dy	dz	.	(2.2)

	ux	uy	uz

Уравнение (2.2) – дифференциальное уравнение траектории по форме совпадает с уравнением для линии тока (2.1). Однако решения их различны: при нахождении уравнения линии тока интегрирование уравнения необходимо проводить для данного момента времени t = const. Линия тока и траек-

тория совпадают при установившемся движении жидк ости.

Трубка тока. Через каждую точку произвольного контура l проведем линии тока (рис. 2.2). Полученная трубчатая поверхность называется трубкой тока. Если контур l мал настолько, что можно считать скорость постоянной в каждой точке охватываемого им сечения, то трубка тока называется элемен-

тарной.

		dS	u2
	l	Sб
		Sб
n			n
u1		S2
u1	S1
		Рисунок 2.2 – Трубка тока

Объемный расход жидкости через произвольное сечение dS с нормалью n элементарной трубки тока (рис. 2.3) вычислим из простых рассуждений: объем жидкости, протекший через сечение dS за время dt, равен объему цилиндра и, т.к. длина его образующей равна udt, то u ndSdt dV , т. е. расход

dQ	dV	u ndS u	dS udS		,	(2.3)
				n
	dt	n

где uп – проекция u на нормаль n ; dSn dS cos u, n						– площадь сечения,

перпендикулярная линиям тока, или «живое сечение».

По аналогии массовый расход жидкости в элементарной трубке тока

vk.com/club152685050 | vk.com/id446425943

dG u ndS undS udSn .

(2.4)

Расход жидкости через произвольную площадку S можно вычислить, просуммировав расходы по элементарным пронизывающим ее трубкам, т. е. объемный расход

Q un dS	(2.5)
S
массовый расход
G un dS .	(2.6)
S

dS n dV

Рисунок 2.3 – Элементарная

трубка тока Размерность: [Q] = м3/c; [G] = кг/с.

Средняя расходная скорость υ в живом сечении Sn связана с объемным расходом соотношением

Q = υSn.

(2.7)

Выбор диаметра трубопровода промышленных сетей принимаются обычно из условий: скорости воды и других маловязких жидкостей 1 3 м/с; воздуха 10 30 м/с; пара до 10 м/с.

Ускорение при движении жидкости вычисляется по формуле

a	du	.	(2.8)

	dt

Если известно поле скоростей (по методу Эйлера), то при вычислении ускорения следует помнить, что u u x, y,z,t . Тогда

a du u dx u y u z u , dt x dt y t z t t

а переменные dx, dy, dz не произвольны, а связаны между собой уравнением траектории (2.2), т. е. dx/dt = ux; dy/dt = uy; dz/dt = uz.

Итак,

vk.com/club152685050 | vk.com/id446425943

a	du	u	u	u	u	u	u	u .	(2.9)
		t		x x		y y
	dt							z z
Составляющая ускорения				u	t	– называется локальным уско-

рением, она характеризует изменение скорости в данной точке пр о-

странства. Очевидно, что при установившемся	движении	u t 0.
Сумма слагаемых ux u x uy u y uz u z –	называется	конвек-

тивным ускорением, она характеризует изменение скорости в да н- ный момент времени вдоль линии тока . Конвективное ускорение всегда равно нулю в прямых каналах (или трубках тока) постоянного сечения при течении несжимаемой жидкости.

В проекциях на оси х, у, z уравнение (2.9) примет вид:

adux

xdt

	ay			duy
				dt

	az			duz
				dt

uxt

uyt

uzt

u ux

uux xy

u uz

x x

ux uy z

yy uz

uz uy z

uxzuy

(2.10)

zuzz

2.2 Уравнение неразрывности

Уравнение неразрывности – это уравнение материального баланса.

Зафиксируем в пространстве произвольный объем V (рис. 2.4). Масса жидкости в объеме

m dV .

	n	u
		u
	dS
dV
dV		V
		V

Рисунок 2.4 – Фиксация произвольного объема V в пространстве (для вывода уравнения неразрывности)

Изменение массы во времени

m		dV dV			(2.11)
t	t
		V	V	t

может произойти только за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность S объема V.

vk.com/club152685050 | vk.com/id446425943

Если n – внешняя нормаль к поверхности dS, то с учетом (2.6) приток

G un dS .				(2.12)
S
Приравняв выражения (2.11) и (2.12), получим уравнение неразрывности
в интегральной форме:
dV		u	dS 0 .	(2.13)
t		n
t
V	S

Слагаемое (2.12) с учетом теоремы о кратных интегралах (теоремы Ост- роградского-Гаусса, см. приложение А) можно преобразовать к виду

un ds

dV div u dV .

Подставим это выражение в (2.13) и просуммируем подынтегральные

функции. Получим

div u dV

Поскольку предел интегрирования V произволен, то последний интеграл может быть равен нулю только при условии, что

	div u 0.	(2.14)
t

Уравнение (2.14) – это уравнение неразрывности в дифференциальной форме.

Для несжимаемой жидкости = const; / t = 0 и уравнение примет

вид
	divu 0					(2.15)
или
u	x	uy	u	z	0 .	(2.16)
				z
		y	z
x		y	z

Для потока несжимаемой жидкости в трубке тока, ограниченной двумя живыми сечениями S1 и S2, уравнение (2.12) принимает вид

un dS 0 ,

или

udScos u, n udScos u, n udScos u, n 0.

Sб

vk.com/club152685050 | vk.com/id446425943

В соответствии с рисунком 2.2 в сечении S1 cos u, n 1, в сечении S2 cos u, n 1, а на поверхности Sб cos u , n 0 (скорость направлена по каса-

тельной к Sб). Поэтому
udScos(u, n) υ1S1;	udScos(u, n) υ2 S2 ;	udScos(u, n) 0
S1	S2	Sб
и уравнение неразрывности для трубки тока
	Q υ1S1 υ2 S2 ,	(2.17)

где υ1, υ2 – средние скорости течения жидкости в сечениях S1 и S2.

2.3 Скорость деформации

В отличие от твердого тела, движение которого рассматривается как сумма поступательного движения со скоростью произвольно выбранной точки (полюса) и вращательного движения вокруг мгновенной оси, проходящей через эту точку, жидкости присуще деформационное движение.

Особенности движения жидкой среды можно выяснить на примере отдельной ее частицы. Если задана скорость в точке А, то скорость жидкости в точке В, отстоящей от точки А (рис. 2.5) на расстоянии dr , можно вычислить по формуле

	uB
dr	В
А	uA
А

Рисунок 2.5 – Схема к определению скорости в точке В

uB uA du uA ux dx uy dy uz dz .

Отсюда следует

du	u dx	u dy	u dz .	(2.18)
	x	y	z

Различие скоростей возникает из-за:

а) растяжения жидкостного элемента (рис. 2.6 а) – линейной деформа-

ции; б) угловой деформации (рис. 2.6 б);

vk.com/club152685050 | vk.com/id446425943

в) вращения элемента без деформации (рис. 2.6 в) – duвр .

Рисунок 2.6 – Геометрическая иллюстрация изменения жидкостного элемента за счет деформации а – линейной; б – угловой и вращения (в)

Следовательно, различие скоростей в результате деформации жидкостного элемента

duдеф du duвр .	(2.19)
Прежде чем приступить к расчету duвр	по известному полю ско-

ростей u = u(x, y, z), вспомним, каков кинематический смысл частных производных.

а) – Кинематический смысл дих/дх

Пусть в системе координат, связанной с точкой 0 жидкости, за время dt точка А переместится и займет положение А1 (рис. 2.7). Тогда удлинение отрезка составит

AA1 uAx u0 x dt .

y
u0x	A uAx A1
0 x	x

Рисунок 2.7 – Схема к определению скорости линейной деформации

Поскольку для бесконечно малого отрезка 0А можно воспользоваться рядом Тейлора, то

u u ux 0 A .

Ax 0 x x

Тогда

AA ux 0 Adt .

1 x

Скорость относительного удлинения отрезка 0А или скорость линейной деформации вдоль оси х

vk.com/club152685050 | vk.com/id446425943

	AA1	ux .	(2.20)
xx
	0 Adt	x

По аналогии выразим скорости линейных деформаций вдоль осей у и z

yy uy y ; zz uz z .

Уравнение неразрывности несжимаемой жидкости (2.16), представленное в виде

xx yy zz 0

свидетельствует о неизменности объема элемента жидкости при его линейной деформации.

б) – Кинематический смысл дих/dy и duy/dx

Пусть за время dt точка А переместится в А1, В – B1, C – C1 (рис. 2.8). Воспользовавшись рядом Тейлора, можно записать

0 A,

u u

x 0C .

0 y

Cx 0 x

С1

uCx

d C

uAy

u0y

d A

u0x

Рисунок 2.8 – Схема к определению угловой

деформации и угловой скорости

Тогда

AA1 uAy u0 y

0 Adt,

CC1 uCx

u0 x dt

x 0Cdt.

В результате относительного движения ребра 0А1 и 0С1 повернутся соответственно на бесконечно малые углы

d A tgd A AA1 0 A uy x dt ; d C tgd C CC1 0C ux y dt ,

т. e. частные производные dux/dy и диy/дх равны угловым скоростям вращения линий 0А и 0С, причем 0С вращается по часовой стрелке, а 0A – против.

d деф

можно вычис-

vk.com/club152685050 | vk.com/id446425943

Поэтому, если принять, что C = d C/dt, то А = – d А/dt. Скорость вращения жидкости в точке 0 относительно оси z

лить, как среднее арифметическое А и C, т.е.

(2.21)

По аналогии нетрудно найти

;

(2.22)

z .

(2.23)

В свою очередь общая относительная деформация сдвига частицы или деформация скашивания прямого угла А0С в А10С1 под действием тангенциальных напряжений yx и xy будет равна сумме этих углов, т.е.

d деф = d A + d C = (диy/дх + dux/dy)dt.

Скоростью угловой деформации в плоскости х – y называется величина

xy 1 d деф .

2 dt

Т. е.

(2.24)

По аналогии, рассмотрев угловые деформации в плоскостях хz и уz,

найдем

;

(2.25)

z .

(2.26)

Вычислим duвр, входящее в (2.19)

duвр dr xi y j z k dx i dy j dz ky dz z dy i z dx x dz j x dy y dx k .

Подставим найденное выражение в (2.19) и запишем его с учетом

vk.com/club152685050 | vk.com/id446425943

(2.18) в проекции на ось х:
du		u	x dx	uy	dy	u	z dz		dz	dy .
	деф x

		x		y		z		y	z
		x		y		z

С учетом (2.21) и (2.23), а также (2.20), (2.24) и (2.25) после преобразований получим

duдеф x xx dx xy dy xz dz .

По аналогии

duдеф y yx dx yy dy yz dz ; duдеф z zx dx zy dy zz dz .

Матрица, составленная из девяти компонентов скоростей линейных и уг-

ловых деформаций, называется тензором скоростей деформаций Т.

	xx		xy		xz
Т		yx		yy		yz	.	(2.27)
		yx		yy		yz
	zx		zy		zz

Она симметрична относительно главной диагонали , т. е. xy = yx;yz = zy; zx = xz, и применительно к несжимаемой жидкости независимо от

ориентации координатных осей

xx yy zz 0.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 В чем заключается различие переменных Лагранжа и Эйлера?

2 В чем разница между линией тока и траекторией? Могут ли они совпадать? 3 В чем различие установившегося и неустановившегося движения?

4 Что такое трубка тока, элементарная струйка жидкости?

5 Дайте определение живого сечения струйки, расхода жидкости и средней по живому сечению скорости.

6 Какой физический закон применительно к жидкости отражает уравнение неразрывности?

7Каков геометрический (кинематический) смысл ux/ x?

8Какое движение называется установившимся?

9Каков геометрический (кинематический) смысл uy/ x – ux/ y?

10Что характеризуют локальное и конвективное ускорения?

11Чем отличается мгновенная местная скорость от средней скорости?

vk.com/club152685050 | vk.com/id446425943

3 ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ НЕСЖИМАЕМОЙ ЖИДКОСТИ

3.1 Силы в жидкости

Силы, действующие в жидкости, принято разделять на два вида.

Силы массовые – это силы, пропорциональные массе жидкости, к которой сила приложена. Примером таких сил является сила инерции F = ma. При составлении уравнений динамики жидкости применяется понятие плотность массовых сил или единичная м а с с о в а я сила , под которыми пони-

мают отношение

f lim F .

m 0 m

Для инерционных сил f a . Размерность [f] = м/c2. Вектор f может быть представлен в виде

f fxi f y j fz k ,

где fx, fy, fz – проекции единичной массовой силы f на оси координат.

Силы поверхностные P – это силы, пропорциональные поверхностям, на которые они действуют. Если в сплошной среде выделить произвольный объем V, то для сохранения его равновесия необходимо к каждому элементу

его поверхности S приложить силу P (см. рис. 3.1).

		n	P
	М		рn
V	М
	S	σn	n
		σn	n
Рисунок 3.1 – Схема к определению
напряжения в точке сплошной среды

Плотность поверхностных сил на площадке с нормалью n называет-

ся напряжением и определяется выражением

p lim P .
n	S 0	S

Напряжение pn может быть разложено на нормальную n и касательнуюn к площадке составляющие.

Компоненты напряжения на площадках, нормальных к координатным осям, называются основными. Так, например, напряжение на площадке с нор-

vk.com/club152685050 | vk.com/id446425943

малью, совпадающей с направлением оси х, px может быть выражено через основные компоненты напряжения в виде

px xi xy j xz k .

По аналогии

py yxi y j yz k ; pz zxi zy j z k .

Первый индекс указывает направление нормали к площадке, второй – ось, на которую спроектировано напряжение pn . Компонент напряжения, считается

положительным, если его направление и направление внешней нормали к площадке совпадают (или оба направления не совпадают) с направлениями осей координат. На рисунке 3.2 показаны положительные направления компонентов напряжения при плоском напряженном состоянии.

	y
y
		yх

х	хy
хy	х
хy
	x
yх	y

Рисунок 3.2 – Положительные направления основных компонентов напряжений

Итак, существует всего девять основных компонентов напряжений. Обычно их представляют в виде матрицы:

	x		xy		xz
pT		yx		y		yz	(3.1)

	zx		zy		z

и называют тензором напряжений.

Тензор напряжений симметричен относительно главной диагонали

(примем без доказательства), т. е.

xy = yx, yz = zy, zx = xz,

и независимо от ориентации координатных осей

x + y + z = const.

Установим взаимосвязь напряжения рn с основными компонентами напряжений. Для этого применим второй закон Ньютона к элементарной массе жидкости, имеющей форму тетраэдра (рис. 3.3) с ребрами dx, dy, dz:

vk.com/club152685050 | vk.com/id446425943

dK	R R	R ,	(3.2)

dt	m	s

где K – количество движения;

R– главный вектор внешних сил представлен в виде суммы массовых Rm и поверхностных RS сил.

Массовые силы Rm этого равенства и количество движения K пропор-

циональны массе жидкости, т. е. величине 1/6 dxdydz. Поверхностные силы, например, на площадке dSx нормальной к оси х

Px px 12 dydz

на порядок больше массовых. Следовательно, в уравнении (3.2) можно пренебречь слагаемыми, пропорциональными массе элементарного тетраэдра.

			z
				px	х
				dz	х	n
				dz		n	pn
				хy			pn
				хy
p	y	yх		xz
	y
y					dy
y				zx	dy		y
		yz	zy	zx			y
		yz	zy
		dx
			pz	z
				z
x
Рисунок 3.3 – К определению взаимо-
связи напряжения pn					с основными ком-
	понентами напряжений

Тогда получим Rs = 0 или

pn dSn px dSx py dSy pz dSz 0.

Разделив это выражение почленно на dSn, и учитывая, что

dS	x	cos x, n ;	dSy	cos y, n ;	dS	z	cos z, n ,

dSn			dSn		dSn

получим

vk.com/club152685050 | vk.com/id446425943

pn pxcos x,n py cos y,n pz cos z,n 0,

или в проекциях на координатные оси
pnx	x cos x,n xy cos y,n xz cos z,n
pny
	yx cos x,n y cos y,n yz cos z,n			(3.3)
pnx
	zx cos x,n zy cos y,n z cos z,n

Давлением в движущейся жидкости называется величина
	p	1	x y z ,	(3.4)

	3

т. е. среднеарифметическое значение сжимающих нормальных основных компонентов напряжений.

Если ньютоновская жидкость находится в покое, то в соответствии с уравнением (1.5) в ней не могут возникнуть касательные напряжения, т. е. xy =yz = zx =0. В этом случае первое из уравнений (3.3) примет вид

pnx = xcos(x, n),

но pnx – проекция рn на ось х, т. е.

pnx = pncos(x, n).

Приравняв два последних выражения, найдем, что pn = x. По аналогии можно показать, что pn = y и pn = z.

Это означает, что в покоящейся жидкости напряжения не зависят от ориентации площадки (закон Паскаля), а давление в ней

p = – pn = – x = – y = – z.

Закон внутреннего трения в обобщенной форме

Это эмпирический закон, устанавливающий связь компонентов тензора скоростей деформаций (2.28) и тензора напряжений (3.1).

Представим выражение (3.1) в виде

рТ рТ

рТ

где

p 0

x p

рТ

; рТ

x p

Тензор рТ

обладает теми же свойствами, что и тензор (2.27), т. е. он

симметричен относительно главной диагонали, а сумма элементов главной

vk.com/club152685050 | vk.com/id446425943

диагонали с учетом определения (3.4) равна нулю.

Простейшая форма связи матриц р1Т и Т – прямая пропорциональность и определяет закон внутреннего трения для ньютоновской жидкости

р1Т 2 Т ,

или в развернутом виде

x		p 2 ux ;
			x

		p 2	uy	;
y
			y

	z	p 2 uz ;
			z

u		y
		y		;
	x			;
	x
	u
	u				(3.5)
		z		;
				;
	y
u		x
u
			.
	z		.
	z

Формулы связи матриц р1Т и Т в цилиндрической (r, , z) и сферической (r, , ) системах координат приведены в приложении В1.

3.2 Уравнение движения в напряжениях

Применим второй закон Ньютона (3.2) к движущейся массе жидкости, заключенной в произвольном объеме V (рис. 3.4).

Рисунок 3.4 – К выводу уравнения

движения в напряжениях

Количество движения K этой жидкости K udV . Поскольку для не-

сжимаемой жидкости V = const и ρ=const, то

udV

dV .

(3.6)

Массовые силы

Rm f dV .

(3.7)

Поверхностные силы RS с учетом теоремы о кратных интегралах Остро- градского-Гаусса (см. приложение А) можно представить в виде

vk.com/club152685050 | vk.com/id446425943

RS pn dS DivpdV .		(3.8)
S	V

Подставив выражения (3.6) – (3.8) в (3.2) и просуммировав подынтегральные функции с учетом того, что объем V произволен, получим уравнение движения в векторной форме записи:

f Divp ,

(3.9)

где

Divp

z .

В проекциях на координатные оси уравнение (3.9) примет вид

dux

;

duy

f y

;

(3.10)

Система уравнений (2.16), (3.5) и (3.10) содержит девять определяемых

переменных: их, иу, иz, x, у, z, хy, yz, zx. Количество уравнений равно количеству неизвестных. Система уравнений, следовательно, замкнута.

Прежде чем приступить к формулировке и решению задач гидромеханики, упростим найденную систему уравнений.

3.3Уравнение движения вязкой несжимаемой жидкости (уравнение Навье-Стокса)

Это уравнение получается путем подстановки выражений (3.5) в (3.10). После преобразований с учетом (2.16) и (1.6) получим

du	x		1 p
	x	fx		2ux ;
dt		fx	x	2ux ;
dt			x

duy			1 p
		f y		2uy ;	(3.11)
dt		f y	y	2uy ;	(3.11)
dt			y

duz			1 p
duz		fz	1 p	2uz .

dt			z
dt			z

где	2	2	2	2	– оператор Лапласа.
где	2	x2	y2	z2	– оператор Лапласа.
		x2	y2	z2
					28

vk.com/club152685050 | vk.com/id446425943

Уравнения (3.11) в цилиндрической (r, , z) и сферической (r, , ) системах координат приведены в приложении В.

Умножив построчно выражения (3.11) на i , j, k и просуммировав их, получим уравнения Навье-Стокса в векторной форме записи:

grad p 2u ,

где

u u

i u

j u

k ;

f f

i f

j f

k ; grad p p i p

Слагаемые уравнения (3.12) характеризуют:

(3.12)

j p k . (3.13)

d u – ускорение (см. (2.9)), или удельную силу инерции; dt

f – единичные массовые силы силового поля, в котором движется жид-

кость;

grad p – поверхностные силы – силы давления;

2u – поверхностные силы – силы вязкостного трения.

При решении конкретных задач существенным моментом является формулирование краевых (граничных) условий. Одним из важных граничных условий является условие прилипания на границе с твердой непроницаемой по-

верхностью – скорость жидкости равна скорости поверхности тела.

3.4 Уравнение энергии

Уравнение энергии составляется на основе закона сохранения энергии: изменение энергии Е жидкости в отсутствие теплообмена с окружающей средой может произойти только за счет работы внешних сил:

dE = dA = Ndt

или
	dE	N ,	(3.14)
	dt

где N – мощность, затрачиваемая внешними силами.

Для гомогенной жидкости в отсутствие изменения агрегатного состояния

E 2 dV cpTdV E0 ,

V V

где cp – теплоемкость жидкости при температуре Т; V – произвольный объем движущейся жидкости; E0 const – прочая внутренняя энергия.

vk.com/club152685050 | vk.com/id446425943

Тогда для несжимаемой жидкости

cpT dV

dV . (3.15)

dt V

Величину N можно представить в виде

N=Nm+Ns,

(3.16)

где Nm – мощность внешних массовых сил

Nm u f dV ;

(3.17)

NS – мощность внешних поверхностных сил

NS u pnds .

С учетом теоремы о кратных интегралах (см. А4.3) можно записать

	u p	x	u py	u p	z
NS		x			z	dV .	(3.18)
NS	x		y	z		dV .	(3.18)
	x		y	z
V

Подставим выражения (3.15) – (3.18) в (3.14) и просуммируем подынтегральные функции всех входящих в (3.14) выражений. Как и ранее, сумма этих функций равна нулю, так как не сделано было каких-либо ограничений на объем V. Получим после простейших преобразований

0 . (3.19)

Согласно (3.9) выражение в скобках равно нулю. Раскроем скалярное произведение последних трех слагаемых. Тогда (3.19) примет вид

cp dt

z .

После подстановки выражений (3.5) окончательно найдем

D ,

(3.20)

где

uy 2

D 2

uy 2 uyx z

u		2	u	z	u	x	2	. (3.21)
	z			z		x		. (3.21)
y			x		z

или, с учетом (2.20, 2.24-2.26)

vk.com/club152685050 \| vk.com/id446425943
D 2 2xx 2yy 2zz 4 2xy 2xz ez2		(3.22)

Функция D называется диссипативной функцией.

Произведение µD характеризует ту часть механической энергии, которая рассеялась, или диссипировалась, в единице объема жидкости, т. е. перешла в тепловую (внутреннюю) энергию. Уравнение (3.20) с учетом (3.22)

позволяет утверждать, что механизм диссипации – это деформации жидкостных частиц.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Классификация сил в гидромеханике.

2 Чем отличается напряженное состояние покоящейся жидкости от движущейся?

3 Какие виды напряжений действуют в жидкости?

4 Что характеризует обобщенный закон внутреннего трения?

5 Какой закон физики лежит в основе уравнения Навье-Стокса ?

6 Каков физический смысл слагаемых уравнения Навье-Стокса в векторной форме?

7 Какой закон физики лежит в основе уравнения энергии? 8 Что следует понимать под диссипацией энергии?

9 Каков механизм диссипации энергии?

4 ГИДРОСТАТИКА

4.1Дифференциальные уравнения равновесия жидкости (уравнения Эйлера)

В состоянии покоя скорость жидкости u = 0. В этом случае уравнения (3.12) и (3.11) соответственно примут вид

f	1		gradp		(4.1)
f			gradp		(4.1)

и
		1 p
fx		1 p		;

		x
		x
		1 p
f y				;	(4.2)
f y		y		;	(4.2)
		y
		1 p
fz				.
fz		z		.
		z

Уравнение (4.1) или система уравнений (4.2) называются уравнениями

Эйлера.

дифференциал давления или

vk.com/club152685050 | vk.com/id446425943

Выясним, при каких условиях жидкость может находиться в равновесии. Для этого умножим построчно уравнения (4.2) на dx, dy, dz и просуммируем их:

	1
fxdx f y dy fz dz		p dx	p dy	p dz .	(4.3)

		x	y	z

Поскольку р = р(х, у, z), то выражение в круглых скобках есть полный dp. Если = const, то правая часть (4.3) равна d(p/ )

fxdx f y dy fz dz d p .

(4.4)

Уравнение (4.4) является основным дифференциальным уравнением гидростатики и имеет решение всегда, т. е. жидкость может находиться в равновесии, если его левая часть представляет собой полный дифференциал

некоторой функции Ф, зависящей от х, у, z. Так как
d	dx	dy	dz ,	(4.5)
	x	y	z

то из сравнения (4.4) и (4.5)следует, что условиями, при которых жидкость может находиться в равновесии, являются:

fx		; f y		; fz	.	(4.6)
	x		y		z

Массовые силы, обладающие свойством (4.6), называются силами, имеющими потенциал, а функция Ф – потенциальной. Итак, жидкость мо-

жет находиться в равновесии только в потенциальном силовом поле. Напомним, что работа сил, имеющих потенциал, равна разности потенциалов (см.

приложение А):
A f dl	fxi f y	j fz k idx jdy kdz fx dx f y dy fz dz
	l	l
		2
		d 2 1 ,
		1

где Ф1 и Ф2 – значения потенциалов в конечных точках пути l.

Поверхность, на которой Ф = const или dФ = 0, называется эквипотен-

циальной или поверхностью уровня. На этой поверхности (4.3) dp = 0 или

р = const, или

fxdx + fydy + fzdz = 0.

(4.6)

Поясним применение дифференциальных уравнений равновесия жидкости (4.4) и (4.6) на конкретных примерах.

vk.com/club152685050 | vk.com/id446425943

4.2Равновесие жидкости в гравитационном поле. Основное уравнение гидростатики

На жидкостные частицы с массой т действует сила тяжести G mg , т.е.

f G m g . Следовательно, (рис. 4.1)
fz = – g; fx = fy = 0.	(4.7)

z0 p0

z p

F=mg

Рисунок 4.1 – К выводу уравнения равновесия жидкости в гравитационном поле

Уравнение поверхности уровня (4.6) примет вид – gdz = 0 или после интегрирования

z = const,

т. е. поверхность уровня представляет собой горизонтальную плоскость. После интегрирования уравнения (4.3) с учетом (4.7) получим

p gz C

или
z	p	const .	(4.8)

	g
Постоянную интегрирования С найдем из граничного условия: при z = z0
р = р0. Тогда С = р0/ + gz0 и
p = p0 + g(z0 – z) =p0 + gh,			(4.9)

где h = z0 – z – глубина погружения точки под поверхностью уровня с известным давлением р0.

Отметим, что уравнение (4.9) называют основным уравнением гидро-

статики.

Частным случаем поверхности уровня является свободная поверхность жидкости, т. е. можно принимать в качестве р0 давление над свободной поверхностью жидкости, a h – глубину погружения точки под свободной поверх-

vk.com/club152685050 | vk.com/id446425943

ностью жидкости. В этом случае второе слагаемое в (4.9) ρgh называется из-

быточным гидростатическим давлением.

Графическое изображение распределения давления по поверхности тела называется эпюрой давления (рис. 4.2).

р0 + gh

Рисунок 4.2 – Эпюра давлений

Уравнение (4.8) имеет простой энергетический смысл.

Первое слагаемое можно представить в виде z = mgz/(mg) = Эп/(mg), т.е. z есть отношение потенциальной энергии положения к весу жидкостной частицы с массой т. Второе слагаемое также характеризует потенциальную энергию, так как численно равно высоте, на которую поднимается жидкостная частица под действием давления р. Итак, слагаемые уравнения (4.8) можно на-

звать: z – удельная потенциальная энергия положения; p/(ρg) – удельная потенциальная энергия давления (сумму z + p/(ρg) – иногда называют «ста-

тический напор»). В такой интерпретации уравнение (4.8) эквивалентно ут-

верждению: в покоящейся жидкости все частицы обладают од инаковой энергией.

4.3 Сообщающиеся сосуды

Пусть в сообщающиеся сосуды залиты две несмешивающиеся жидкости с плотностями 1 и 2 (рис. 4.3). Отметим, что в данной задаче сосуды являются сообщающимися только по жидкости с плотностью ρ2.

	рр1	р2
h1		1
h1	A	h2
	A	h2
2		B
2
		Поверхность
		уровня
Рисунок 4.3 – Равновесие жид-
кости в сообщающихся сосудах

Установим условие равновесия жидкости при давлениях в сосудах над жидкостями p1 и р2. Предельное верхнее положение поверхности уровня в слу-

перепад уровней жидкости в трубках

Так как

vk.com/club152685050 | vk.com/id446425943

чае 1 2 показано на рисунке 4.3. При этом p = const, т. е. pА = pВ. В соответствие с основным уравнением гидростатики

pА = р1 + 1gh1; pB= р2 + 2gh2.

Тогда условие равновесия можно записать в виде

р1 + 1gh1 = р2 + 2gh2.

Принцип сообщающихся сосудов часто применяется в измерительной технике. Прибор, изображенный на рисунке 4.4, называется U-образным мано-

метром.

рат

Поверхность A B уровня

Рисунок 4.4 – U-образный манометр

рА = рВ или p = pат + ρgh

прибора составит h = (p – pат)/(ρg), т. е. прибор измеряет избыточное давление над атмосферным или манометрическое давление.

Если p pат, то уровни жидкости в трубках приборах установятся так,

как показано на рисунке 4.5. В этом случае h = (pат – p)/( g), т. е. прибор измеряет вакуум или давление, не достающее до атмосферного.

рат

р1

р2






Рисунок 4.5 – U-образ-					Рисунок 4.6 – Дифференци-
ный вакуумметр					альный манометр

Прибор, показанный на рисунке 4.6, называется дифференциальным манометром (дифманометром). Он измеряет разность давлений в двух сравниваемых точках:

h = (p1 – p2)/( g).

vk.com/club152685050 | vk.com/id446425943

Во всех приведенных примерах предполагалось, что в сосудах, давление в которых измерялось, находился газ, плотность которого значительно меньше плотности жидкости, залитой в прибор.

4.4 Равновесие жидкости в центробежном поле

На жидкостные частицы, находящиеся во вращающемся с постоянной скоростью вокруг вертикальной оси цилиндрическом стакане, действуют сила

тяжести mg и центробежная сила m 2r (рис. 4.7).
	z	ω
		ω
		p0
z0		m z
z0	0
	0		y
		mg	y
		mg
x
		r
	0	x	y
	0	y m
	x	m 2r
	x
Рисунок 4.7 – Равновесие жид-
кости в центробежном поле

Следовательно, в этом случае

fx = 2rcos(r, x); fy = 2rcos(r, y); fz = g.

или

fx = 2x; fy = 2y.

Подставим эти выражения в (4.3) и проинтегрируем последнее. Получим

	p	2 x2		2 y2		gz C	(4.10)
				2 y2		gz C	(4.10)
			2		2
или
		p	2r2		gz C		(4.11)
			2r2		gz C		(4.11)
				2

При р = const уравнение (4.10) преобразуется в уравнение поверхности уровня – уравнение параболоида вращения. Постоянную интегрирования С в (4.11) найдем из начального условия р = р0 при r = 0 и z = z0.

Тогда

vk.com/club152685050 | vk.com/id446425943

pp0 12 2r2 g z0 z .

4.5Сила давления на плоскую поверхность тела

Силы давления, действующие на каждый элемент поверхности dS (рис. 4.8), параллельны, т. е. суммирование их можно проводить алгебраически:

P pdS

(4.12)

и результирующая сила Р всегда направлена по внутренней нормали к плоской поверхности. Подставим (4.9) в (4.12). С учетом того, что h = ysin , получим

P p0	gy sin dS p0S gsin ydS .
S				S
			p0
			α	0
			α
	hC	h
hD		P	yС
			y	x
				yD
				dS
				C
y			D	S
y				S

Рисунок 4.8 – Схема определения силы давления на плоскую поверхность тела

Статический момент площади S относительно оси х можно записать в ви-

де

ydS SyC ,

где точка С – центр тяжести площади S.

Поскольку yСsin = hС, то, обозначив силу от внешнего давления – Р0 = p0S, а силу от гидростатического (избыточного) давления – Рг = ρghСS, будем иметь

Р = Р0 + Pг; Р = (p0 + ρghС) S = pСS.

(4.13)

Из (4.13) следует, что для вычисления величины равнодействующей силы давления необходимо знать давление рС в центре тяжести площади.

Найдем точку приложения равнодействующей силы давления. Очевидно, что составляющая ее P0 = p0S приложена в точке С. Для определения центра

vk.com/club152685050 | vk.com/id446425943

давления (точки D) составляющей Рг составим уравнение моментов сил относительно оси х:

Pг yD y ghdS

			S
или, т. к. Pг = ghcS и h = ysin , то
y		1		y2dS	I0x	,	(4.15)
y	D	y S		y2dS		,	(4.15)
	D				y S
					y S
		c	S		c
			S

где I0х – момент инерции площади S относительно оси х. Поскольку

I0x IC yD y2S ,

то после подстановки этого выражения в (4.15) получим

yD yC yICS ,

где IС – момент инерции площади относительно горизонтальной оси, проходящей через центр тяжести площади.

4.6 Сила давления на цилиндрическую поверхность тела

Силы давления, действующие на элементы криволинейной поверхности, необходимо суммировать геометрически:

P pndS ,	(4.16)
S

где n – единичный вектор, направленный по внутренней нормали к поверхности.

Вычислим, горизонтальную составляющую Рy силы Р. Для этого спроек-

тируем (4.16) на ось y:
Py pcos y,n dS pdS y .		(4.17)
S	S y

Здесь dSy – проекция dS на вертикальную плоскость. Подставив в (4.17) уравнение (4.9), после интегрирования найдем

Py = P0y+Pгy = (p0+ ghCy)Sy.

По аналогии с предыдущей задачей найдем положения линий действия составляющих Р0y и Ргy: сила Р0y приложена в центре тяжести площади Sy на вертикальную плоскость, сила Ргy приложена в точке Dy (рис. 4.9):

hDz hCy	ICy	,
hDz hCy	Sy hCy	,
	Sy hCy
38

vk.com/club152685050 | vk.com/id446425943

где IСy – момент инерции площади Sy относительно горизонтальной оси, проходящей через ее центр тяжести.

Спроектируем слагаемые уравнения (4.16) на вертикальную ось z:

Pz pcos z,n dS pdSz .

S Sz

hCy hDy

dS	Sy
dS	Cy
	Cy	Dy
Sz	n	dP
	Cz	dP
	Cz

Рисунок 4.8 – Схема определения силы давления на цилиндрическую поверхность тела

С учетом (4.9) получим

Pz p0Sz g hdSz p0Sz ghW P0z Pгz ,

где W – объем тела давления, т. е. объем, заключенный между криволинейной поверхностью, поверхностью уровня с давлением р0 и вертикальными проектирующими поверхностями, проведенными через границы контур S.

Составляющая силы Pгz = gW приложена в точке Dz – центре тяжести объема W и направлена вниз в том случае, если в объеме тела давления находится жидкость, и вверх, если в W нет жидкости. Составляющая P0z=p0Sz проходит через точку Cz – центр тяжести площади Sz.

4.7 Закон Архимеда

Если пронизать тело, погруженное в жидкость, вертикальным цилиндром с основанием dSz, то на площадки dS1 и dS2, отсекаемые на поверхности тела (рис. 4.10), действуют соответственно гидростатические силы, вертикальные составляющие которых

dP1z = gh1Sг и dP2z = gh2Sг.

Результирующая сила направлена вверх и равна

dPz = dP2z – dPlz = g(h2 – h1)dSz = gdW,

vk.com/club152685050 | vk.com/id446425943

где dW – объем тела, отсекаемый элементарным цилиндром.

z	p0	dSz

	h1	dP1

h2		dS1
	h
		dS2

dP2

Рисунок 4.10 – К выводу закона Архимеда

Просуммировав силы по всей поверхности тела, найдем, что

Pz = gW,

где W – объем тела, погруженного в жидкость. КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Дайте понятие эквипотенциальной поверхности. Каково ее уравнение?

2 Может ли движущаяся жидкость находиться в равновесии? Если может, то при каких условиях?

3 Какова энергетическая интерпретация основного уравнения гидростатики?

4 Какова математическая формулировка закона сообщающихся сосудов?

5 Есть ли разница в понятиях "гидростатический напор" и "пьезометрический напор"? Если есть, то в чем их различие?

6 Что следует понимать под абсолютным, избыточным и вакуумметрическим давлением?

7 В каких случаях плоскость пьезометрического напора располагается выше и ниже свободной поверхности покоящейся жидкости?

8 Отличается ли пьезометрическая высота от вакуумметрической?

9 Как рассчитать силу давления на плоскую стенку?

10 Как определяются составляющие силы давления покоящейся жидкости на криволинейную поверхность?

11 Что такое тело давления?

5 ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ

5.1 Уравнение движения идеальной жидкости (уравнение Эйлера)

Поскольку в идеальной жидкости v = = 0, то уравнения (3.10) и (3.11) примут соответственно вид

du	f	1	gradp	(5.1)

dt

vk.com/club152685050 | vk.com/id446425943

dux		f		1 p	;
			x
dt				x
dt				x


duy		f y		1 p
					;	(5.2)
dt				y	;	(5.2)
dt				y
du	z	fz		1 p
	z				.
dt				z	.
dt				z

Уравнения (5.1) и (5.2) – это уравнения Эйлера для движущейся идеальной жидкости.

5.2 Уравнение Бернулли для плоского установившегося течения

Движение называется плоским, если линии тока лежат в плоскости и не изменяют своей конфигурации при параллельном переносе этой плоскости.

Если, например, линии тока лежат в плоскости xz, то uy = 0 и система уравнений (5.2) примет вид

	du	x	fx			1 p
		x						;
	dt					x		;
	dt					x			(5.3)
	duz					1	p		(5.3)
	duz		f	z		1		.
			f					.
	dt					z


При установившемся движении u					t 0 и для расчета ускорений в (5.3)
можно применить зависимости (см. уравнения (2.10)):


dux		u		ux u		ux		;
		u		ux u				;
dt			x	x	z	z
			x		z
									(5.4)
duz	u			uz u		uz	.
	u			uz u			.
dt			x	x	z	z
dt				x		z

Выясним, при каких условиях уравнения (5.3) можно представить в виде полного дифференциала некоторой функции, т. е. установить их общее решение. Для этого умножим построчно уравнения (5.3) на dx и dz и сложим. Получим

du	x		du	z		p
		dx			dz d		,	(5.5)

dt			dt

где выражение dФ = fxdx + fzdz справедливо в случае, когда поле массовых сил потенциально.

Подставим в (5.5) выражения (5.4). Прибавим к левой части и вычтем из

vk.com/club152685050 | vk.com/id446425943

нее слагаемые	u	z	uz dx	и u	z	uz	dz . После некоторых преобразований полу-

			x			z
чим

d u2 ux2 z

u	z		p
		uz dx uxdz d		.	(5.6)

x

Итак, искомое условие выполняется тогда, когда второе слагаемое в (5.6) равно нулю, т. е. в двух случаях:

1 Сомножитель uzdx – uxdz = 0 или dx dz , т. е. в случае, когда интегри- ux uz

рование (5.6) проводится вдоль линии тока (см. уравнение 2.1).

2 Сомножитель ux uz 2 y 0 (см. уравнение (2.22)), т. е. отсутству-

z x

ет вращательное движение жидкостных частиц. Отметим, что такое дви-

жение называется безвихревым или потенциальным.

При выполнении условий 1 или 2 уравнение (5.6) можно записать в виде

u2		p	0,
d				(5.7)

	2

т. е. в идеальной жидкости при течении вдоль линии тока или в случае безвихревого движения во всем пространстве выполняется условие

u2	p	const .	(5.8)
2

Для гравитационного поля и при вертикальном расположении

оси z fx = 0; fz = – g, т. е. dФ = fxdx + fzdz = – gdz или Ф = – gz+C1.

С учетом этого выражения уравнение (5.8) можно записать в виде

z	p	u2	C .	(5.9)
	g
		2g
Уравнение (5.9) – это уравнение Бернулли. Поясним энергетический
смысл уравнения Бернулли.
Первые два слагаемых в (5.9) имеют тот же смысл,				что и в уравнении

(4.8), т. е.: z – удельная потенциальная энергия положения, p/( g) – удельная потенциальная энергия давления. Третье слагаемое в уравнении (5.9) с

учетом простого преобразования

u2 / 2g 12 mu2 / mg Эк / mg ,

представляет собой отношение кинетической энергии к весу жидкостной частицы, или удельную кинетическую энергию. Следовательно, сумму всех трех

vk.com/club152685050 | vk.com/id446425943

слагаемых можно назвать удельной полной энергией:

e z	p	u2	.	(5.10)
	g
		2g

В такой интерпретации уравнение (5.9) – это уравнение сохранения ме-

ханической энергии.

Отметим, что слагаемые уравнения (5.9) имеют размерность [м]. Поэтому введены термины: z + p/(ρg) – статический напор, а u2/(2g) – динамический напор.

5.3 Плоские потенциальные течения

При изучении плоских течений как реальной, так и идеальной жидкости,

удобно ввести функцию тока , которая связана со скоростями их и uy соотношениями

ux		;	uy	.	(5.11)
	y			x

Соотношения (5.11) всегда удовлетворяют уравнению неразрывности, а уравнения движения (5.2) преобразуются в систему двух уравнений с двумя

скалярными переменными p и .

Функция тока = const на линии тока. Это легко увидеть, если подставить (5.11) в уравнение для линии тока uxdy – uydx = 0:


	dy	dx d 0 .
y		x

Ранее было показано, что при плоском безвихревом или потенциальном течении идеальной жидкости, когда выполняется условие

2		u	x	uy	0 ,	(5.12)
	z
		y		x

интеграл уравнения движения имеет вид (5.8) – уравнение Бернулли, которое взаимосвязывает две величины: р и u. Поэтому задача сводится к интегрированию уравнения неразрывности.

При выполнении условия (5.12) существует такая функция , что

ux		;	uy	.	(5.13)
	x			y

В этом не трудно убедиться, подставив (5.13) в (5.12). Функция на-

зывается потенциалом скорости, а течение при выполнении условия (5.11) – потенциальным.

Подстановкой уравнений (5.13) в уравнение неразрывности (2.16) получим уравнение Лапласа:

vk.com/club152685050 | vk.com/id446425943

2		2	0,	(5.14)
x2		y2

решение которого дает распределение , а, следовательно, и скоростей по (5.13) и давлений (по (5.9)), т. е. полное решение задачи гидродинамики.

Подстановка уравнений (5.11) в условие (5.12) дает уравнение Лапласа:

2		2	0 .	(5.15)
x2		y2

Без доказательства примем, что линии = const и = const взаимно

перпендикулярны (функции и – ортогональны), т. е. grad grad 0. Из теории функций комплексной переменной известно, что любая аналитическая функция w удовлетворяет уравнению Лапласа и, если ее представить в виде

w x iz R x,z iI x,z ,

где i 1, то функции R и I также удовлетворяют уравнению Лапласа и, кроме того, ортогональны. Поэтому, если при решении задачи гидродинамики установлено, что = R, то должно выполняться условие = I, или, если = I, то = R.

Рассмотрим некоторые простейшие примеры:

a) w(x + iz) = a(x+iz) = ax+iaz, где а = const.

Если = ах, то ux = / x = a; uy = 0 и = az.

Уравнение линий постоянного потенциала скорости ( = const) – x = const (рис. 5.1).

y	= const	y	= const
y	= const	y
	= const		x
	x		= const
Рисунок 5.1 – Течение жидкости		Рисунок 5.2 – Течение от диполя
	вдоль оси х

Уравнение для линий тока ( = const) имеет вид y = const, т. е. рассмотренный случай – это случай течения жидкости вдоль оси х с постоянной во всем пространстве скоростью;

б) w x iy	a	a x iy	ax	i	ay	.

	x iy	x iy x iy	x2 y2		x2 y2

vk.com/club152685050 | vk.com/id446425943

Если

, то

x2 y2

Уравнение для линии тока ( = const) имеет вид

C или x2

a 2

x2 y2

т. е. уравнение окружности (рис. 5.2).

Уравнение линии постоянного потенциала скорости ( = const) также преобразуется к виду

a 2

Полученное течение называется течением от диполя;

в) w x iz a x iy

a x

ia y

x iy

x2 y2

, то уравнение линий тока ( = С)

Если ax 1

x2 y2

ay 1

x2 y2

В частном случае при С = 0 уравнение линии тока имеет два решения: y = 0; x2 + y2 = 1.

Поскольку на твердой поверхности при течении идеальной жидкости нормальная составляющая скорости равна нулю, то уравнение контура твердого тела является также и уравнением для линии тока. Поэтому в рассмотренных примерах любая линия тока может быть взята в качестве контура обтекаемой жидкостью поверхности тела.

Если в качестве контура твердого тела принять окружность с радиусом r0= 1, т. е. зависимость x2 + y2 = 1, то с внешней стороны от окружности получим картину обтекания цилиндра потенциальным потоком, представленную на рисунке 5.3. Параметры невозмущенного потока при х = – : скорость u0 = а, давление р0.

Решение задач по гидромеханике сводится обычно к нахождению силы взаимодействия жидкости с обтекаемым телом. Наметим дальнейшие шаги в решении задачи обтекания цилиндра единичного радиуса. Зная уравнение для

, легко найти ux = / x и uy = / y. При нахождении распределения скоростей по поверхности цилиндра удобно перейти к цилиндрическим координатам x = rcos ; y = rsin (см. рис. 5.3 и приложение В).

vk.com/club152685050 | vk.com/id446425943

		y
	x2 + y2 = 1		=const
	x2 + y2 = 1			uD = 2а
		D		uD = 2а
		D
	= 0			= 0	x
u0 = а	r0=1				x
u0 = а	A			B
р0	A			B
		C		uC = 2а
				uC = 2а
Рисунок 5.3 – Поперечное обтекание цилиндра по-
	тенциальным потоком идеальной жидкости

Тогда на поверхности цилиндра x = соs ; y = sin ; ux1 = 2asin2 ; uy1 = – 2asin cos . Нетрудно вычислить

u2	u2	u2	4a2sin2	(5.16)
1	x1	z1

Уравнение Бернулли в случае, когда плоскость хy горизонтальна, имеет

вид

p u2 const

g 2g

Приравняв удельные энергии невозмущенного потока и жидкости на поверхности цилиндра, найдем

p	2 p p0	1 4sin2	(5.17)
p	u2	1 4sin2	(5.17)
	u2
	0

На рисунке 5.4 приведены теоретические и экспериментальные распределения скорости и давлений по поверхности цилиндра.

Сила сопротивления

Px рcos dS

с учетом (5.17), т.е. для идеальной жидкости лишенной сил трения, окажется равной нулю. Это решение получило название «парадокс Даламбера».

Как следует из рисунка 5.4 поля скоростей и давлений при обтекании ци-

vk.com/club152685050 | vk.com/id446425943

линдра идеальной и реальной вязкой жидкостью существенно отличаются друг

от друга. При больших числах Re = u02r0/ цилиндр плохо обтекается жидкостью. Поток реальной жидкости срывается с поверхности цилиндра. Положение

точки отрыва зависит от числа Re. Если Re < Reкр 2 105, то точка отрыва находится в кормовой области цилиндра, если Re > Reкр, то в лобовой части. При этом сопротивление резко уменьшается (см. рис. 6.12).

						Теория
р					u/u0
р						2
						2
			u/u0			А	В	х
1						1
				Теория		Re>Reкр
0		Re=2,1 105				0
		Re=2,1 105
– 1					2	– 1
– 1						– 1
	р					Re<Reкр
						Re<Reкр
– 2						– 2
	1			Re=1,1 10		5
– 3				Re=1,1 10		– 3
180	150	120	90	60	30

А 210 240 270 300 330 В

1 – при обтекании потенциальным потоком идеаль-

ной жидкостью; 2 – при обтекании вязкой жидкостью

Рисунок 5.4 – Распределение скорости и давления по поверхности цилиндра

Отметим, что в лобовой части цилиндра (при < 40 ) распределения давлений для идеальной и для реальной жидкости близки. При = 0 давление на поверхности цилиндра увеличивается на величину ρu02/2, которая называется динамическим давлением. Очевидно, что это вызвано полным торможением жидкостного потока, с преобразованием кинетической энергии в потенциальную. Сумма p + ρgz + ρu2/2, т.е. статического и динамического давлений, называется полным давлением.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Какое движение жидкости называют плоскопараллельным?

2 Какое движение жидкости называют безвихревым?

3 Какое движение жидкости называют потенциальным?

4 Что определяют функция тока и потенциал скорости?

5 Физический смысл уравнения Бернулли и его слагаемых?

6 В чем суть парадокса Даламбера?

7 С помощью каких предположений можно получить решение уравнений Эйлера в виде интеграла Бернулли?

8 Что такое динамический, статический и полный напор? 9 Что такое динамическое, статическое и полное давление?

< υ < υкр2

υкр1

vk.com/club152685050 | vk.com/id446425943

6 ОБЩИЕ ЗАКОНОМЕРНОСТИ ДИНАМИКИ ВЯЗКОЙ ЖИДКОСТИ

6.1 Два режима течения

Опыты, проведенные Рейнольдсом на установке, схема которой представлена на рисунке 6.1, позволили установить, что при υ < υкр1 в трубке наблюдается слоистое, ламинарное течение жидкости.

Вводимая в поток подкрашенная жидкость размывается только за счет








			а)			б)

а) – ламинарный режим течения;

б) – турбулентный режим

Рисунок 6.1 – Схема установки Рейнольдса

диффузии. При υ > υкр2 > υкр1 размыв краски происходит практически мгновенно. В потоке наблюдаются пульсации скорости и перемешивание слоев. Такой режим называется турбулентным. В области скоростей режим течения может быть турбулентным, либо ламинарным. При увеличении скорости от значений и υ < υкр1 в этой области сохраняется ламинарный режим, а при уменьшении от значений υ > υкр2 – сохраняется турбулентный.

Опыты позволили установить, что режим течения зависит не только от υ,

но и от вязкости и диаметра трубы d. При Re = υd/ > υкр1d/ = Reкр1 = 2320 – ламинарный режим, при Re >> Reкр2 – турбулентный режим. Величина

Reкр2 зависит от условий проведения опытов, от качества исполнения установки, от внесения возмущений в поток. По мере улучшения качества установок число Reкр2 увеличивалось и составляло 10000, 13800, 50000 и т. д.

В промышленных трубопроводах условия течения жидкости далеки от идеальных, всегда присутствуют вибрации установок, пульсации расходов. Это приводит к развитию турбулентности практически при Re > Reкр1. Поэтому

vk.com/club152685050 | vk.com/id446425943

при расчете промышленных трубопроводов можно принимать, что при Re 2320 – режим ламинарный, а при Re > 2320 – турбулентный.

При расчете числа Рейнольдса для каналов некруглого сечения в качестве характерного размера живого сечения принимается эквивалентный диаметр dэ,

определяемый по формуле dэ = 4Sn/ , где Sn – площадь живого сечения, – периметр сечения, смоченный жидкостью.

Отметим, что численное значение Reкр1 зависит от формы поперечного сечения канала (см. табл. 6.1)).

Таблица 6.1 – Критическое число Рейнольдса для каналов различной формы

Тип канала	Reкр1

Кольцевой	2000 – 2800

Прямоугольный	2000 – 2300

Треугольный с αmin >45°	~2000

6.2Уравнение турбулентного течения несжимаемой жидкости (уравнение Рейнольдса)

Турбулентное течение жидкости – это неустановившееся течение. При решении практических задач обычно бывают заданы средние во времени значения скоростей u и напряжений , . Уравнение движения, выраженное через u и p , было выведено Рейнольдсом. Приведем преобразования для урав-

нения движения в напряжениях (3.10) в проекции на ось x. С учетом (2.10) и (2.16) ускорение dux/dt можно представить в виде

du	x	u	x	ux2	uxuy	uxuz	(6.1)
				x	y	z
dt		t

Истинные значения скоростей и напряжений с осредненными связаны зависимостями:

	;

ux ux ux		x x x ;
			(6.2)

uy uy uy ;		xy xy xy ;
	;

uz uz uz		xz xz xz .

Здесь их', иу', uz', х', xy', xz' – пульсационные составляющие. Подставим уравнения (6.1) и (6.2) в (3.10) и проведем операцию сглажи-

вания (осреднения) функций по правилам: если a a a и b b b , то

a a; ab

a b a b ;

0; a

x .

После преобразований получим

vk.com/club152685050 | vk.com/id446425943

dux

(6.3)

x uxux

xy uxuy

xz uxuz

Итак, при турбулентном течении жидкости в результате пульсаций скоростей возникают дополнительные или турбулентные напряжения.

Аналогичные только что приведенным преобразования со всеми уравнениями (3.10) позволяют выявить шесть независимых компонентов турбулентных напряжений:

uxux

uxuy

uxuz

uyux

uyuy

uyuz

ртурб

(6.4)

uzux

uzuy

uzuz

Если усреднить выражения (3.5) и подставить их в (6.3), то получим сглаженную форму уравнения Навье-Стокса, которое называется уравнением Рейнольдса. Приведем вид этого уравнения только в проекции на ось x:

dux

1 p

uxux

uxuy

uxuz .

Система, состоящая из трех уравнений Рейнольдса и уравнения неразрывности в виде

ux uy uz 0x y z

не замкнута. Для замыкания ее необходимы еще шесть уравнений.

6.3 О моделировании в гидромеханике

Два процесса подобны, если описываются тождественными уравнениями с тождественными граничными условиями и протекают в геомет-

рически подобной обстановке. Зная условия подобия, можно исследовать модельный аппарат, машину, а потом перенести результаты испытаний на реальный проектируемый объект.

Для выявления условий гидромеханического подобия преобразуем уравнение Навье-Стокса (3.11) к безразмерному виду, посредством выбора некоторых характерных величин (масштабов) и введения системы безразмерных величин, определенных следующим образом:

L масштаб длины; x x L; y y		L; z z L;
U масштаб скорости; ux ux	U ; uy uy U ; uz uz U ;
T масштаб времени; t t T ;
g масштаб массовых сил; fx	fx	g ; f y f y	g ; fz f y
p0 масштаба давлений; p p	p0 .

(6.5)

Здесь величины, отмеченные волнистой линией, безразмерные.

vk.com/club152685050 | vk.com/id446425943

Возьмем первое из уравнений (3.11) и подставим в него (2.9). Далее с учетом (6.5) и преобразований, связанных с вынесением масштабов из-под знаков дифференциала, после умножения всех слагаемых на L/U2 получим

x u

, (6.6)

x x

z z

x Re

где

; Fr

U 2

; Eu

; Re

U 2

Безразмерные коэффициенты Sh, Fr, Eu, Re называются числами подобия (иногда – критериями подобия) и носят имена ученых: Sh – число Струхаля; Fr – число Фруда; Еu – число Эйлера; Re – число Рейнольдса. Равенства чисел подобия в уравнении (6.6) и геометрическое подобие модели и объекта достаточно для обеспечения подобия гидромеханических процессов.

Поскольку каждое из слагаемых уравнения Навье-Стокса характеризует одну из сил, действующих в жидкости, то числа подобия характеризуют их отношения. Так,

Sh	f	и. л	; Fr	f	и. к	; Eu	f p	; Re	f	и. к	,

	fи. к				fm		fи. к		fтр

где fи. л – сила инерции, вызванная локальным ускорением;

fи. к – сила инерции, вызванная конвективным ускорением; fm – массовая сила;

fтр – сила вязкостного трения; fр – сила давления.

Полную модель для объекта не всегда удается получить.

Например, пусть Lо/Lм =102 (индексы: о – объект; м – модель). Тогда из равенства чисел Фруда Uо2/(gLо) = Uм2/(gLм) следует, что Uо/Uм = (Lо/Lм)0,5

= 10; из равенства чисел Рейнольдса UоLо/ о = UмLм/ м о/ м = UоLо/(UмLм) = 103 испытания модели надо проводить в среде, вязкость которой значительно ниже вязкости среды объекта, что не всегда удается реализовать.

6.4 Решение задач гидродинамики методом теории подобия

При интегрировании дифференциальных уравнений в определенных пределах решение всегда содержит лишь ту или иную комбинацию коэффициентов уравнения и граничные условия.

Поясним это на легко решаемом примере. Дано уравнение

y a0 a1x

vk.com/club152685050 | vk.com/id446425943

и начальное условие при х = х0 у =у0. Вычислить y1 при х = x1. Решение задачи имеет вид

y1 y0 a0 (x1 x0 ) a1(x12 x02 )

или y1 = f(x1, x0, y0, a0, a1), или F(x1, x0, y0, a0, a1) = 0.

По аналогии можно утверждать, что и решение уравнения Навье-Стокса можно записать в виде F(Sh; Fr; Eu; Re; Г1; Г2; ...) = 0, где Г1; Г2 - отношения различных размеров объекта к масштабу L, определяющие его геометрию (геометрические симплексы).

Покажем, что применение уравнения движения в безразмерном виде существенно сокращает объем экспериментальных исследований, необходимых для уточнения вида искомой функции. Рассмотрим несколько примеров.

а) Установившееся ламинарное течение жидкости в горизонтальной трубе. В качестве масштабов при решении этой задачи можно принять L = d, U= υ (d – диаметр трубы; υ – средняя расходная скорость). Поскольку dux dt 0

и fx 0, то уравнение (6.6) существенно упростится и его можно привести к виду

Eu Re px 2ux

т. е. получим уравнение с одним коэффициентом Eu Re. Решение следует искать в виде F(Eu Re; l/d) = 0, где l – длина трубы, или Eu Re =f(l/d). Физиче-

ски очевидно, что р 1, т. е. f(l/d) =C l/d и расчетное уравнение содержит только один неизвестный коэффициент С:

p	C l	υ2 C υl .	(6.7)

	Re d	d 2

б) Установившееся турбулентное течение в горизонтальной трубе. Если подставить уравнение (3.5) в (6.3) и привести последнее к безразмерному виду, то при dux dt 0

0 Eu

uxux

uxuy

uxuz .

Это уравнение содержит два независимых коэффициента Еu и Re и его

решение следует искать в виде (Eu; Re; l/d) = 0 или Eu = f(Re) l/d, или
p f Re	l	υ2 .	(6.8)
	d

в) Установившийся турбулентный режим перемешивания жидкости в аппарате с мешалкой (рис. 6.2).

vk.com/club152685050 | vk.com/id446425943

В отличие от предыдущей задачи в уравнении сохраняется сл а-

гаемое Fr–1 f и решение следует искать в виде
	D		H		b		h		0 ,
F Eu; Re; Fr;		;		;		;		; n		(6.9)
F Eu; Re; Fr;		;		;		;		; n		(6.9)
	d		d		d		d

где n – число лопастей.

Рисунок 6.2 – Схема аппарата с лопастной мещалкой

Выберем масштабы: L = d; U = d; p0 – средний перепад давлений на лопасти. Сила F, действующая на n лопастей, пропорциональна p0 b d n, а мощность N на перемешивание жидкости N~ F d, т. е.

р	N	d	1	.

0	d 3 b n

С учетом выбранных масштабов числа подобия примут вид

Re	d 2	; Fr	2d	; Eu k		d 1	,

			g		N b n

где kN N .

3d 5

Подставив в (6.9) преобразованное число Еu, решим его относительно kN

	D		H		b		h
kN f Re; Fr;		;		;		;		; n .
kN f Re; Fr;	d	;	d	;	d	;	d	; n .
	d		d		d		d

Вид этой зависимости чаще всего раскрывают на основе экспериментальных исследований.

Некоторые задачи гидромеханики удается решить аналитически. Рассмотрим простейшие из них.

vk.com/club152685050 | vk.com/id446425943

6.5. Ламинарное безнапорное течение Куэтта

Это установившееся течение жидкости между двух параллельных пластин под действием движения одной из них (см. рис. 1.1). В уравнениях (3.11) uz = uy = 0; fx = 0; dux/dt = 0; p/ x = 0. Следовательно, уравнение движения в проекции на ось х примет вид

0 2ux .z2

Интегрируем

ux C1; ux C1z C2 .

Граничные условия: при z = 0 ux = 0, отсюда С2 = 0;

при z = ux = u0, тогда С1 = u0/ .

Итак, распределение скоростей в зазоре, как ранее и предполагалось, линейно и подчиняется зависимости ux = u0z/ . Из (3.5) следует, что ux/ z= xz/ и, так как ux/ z = С1 = const, то ясно, что при течении Куэтта xz = 0=μu0/ = const ( 0 – касательное напряжение на стенке канала), а силу F можно вычислить по (1.4).

6.6Равномерное ламинарное течение в плоскопараллельном (щелевом) канале

При установившемся течении жидкости вдоль оси (рис. 6.3) в горизонтальном канале uy = uz = 0; fx = 0; dux/dt = 0.

0	z	υ
	z0	υ
	z0
		ux
		umax

–z0

Рисунок 6.3 – Ламинарное течение в плоском канале

Уравнение движения (3.12) в проекции на ось х примет вид

	1 p		2u	x
0		x			(6.9)
			z2

На ось z

vk.com/club152685050 | vk.com/id446425943

0 1 p ,

т.е. в живом сечении

р = С(х) – gz.

Из этой зависимости следует, что распределение давлений в живом сечении канала такое же, как в покоящейся жидкости. Вычислим производную по x.

p C х ,x x

следовательно др/дх не зависит от z. Проинтегрируем (6.9) дважды по z. С учетом (1.5) – (1.6) и граничных условий:

при z = 0 ux/ z = 0; = 0; при z = z0 их = 0; = 0

получим уравнения для расчета распределения скоростей и напряжений

ux	1 p	z02	z2 ; 0	z		.

	2 x			z	0

Максимальная скорость (при z = 0):

u	1	p z2 .

max	2 x 0

Вычислим расход жидкости в канале при ширине его В:

	z							p z03 .
Q 2B 0 uxdz						2B
Q 2B 0 uxdz
	0					3 x
	0
Средняя расходная скорость
υ	Q				1		p z2 .
υ							p z2 .
	2z		B		3 x			0
		0
Откуда
	p			3 υ				(6.10)
	x			z2				(6.10)
	x			z2
				0

Перепад давлений в канале длиной l найдем, проинтегрировав (6.10) по х:

p p	p		3 υl	(6.11)

1	2		z2

		0

где р1 и p2 – давление в начале и конце канала соответственно. Уравнение (6.11) – искомая расчетная зависимость.

vk.com/club152685050 | vk.com/id446425943

При решении практических задач для вычисления потерь давления при течении жидкости в горизонтальных каналах часто применяется уравнение Дарси-Вейсбаха:

p	l	υ2
		.	(6.12)
		.	(6.12)
	dэ	2

С учетом того, что для плоского канала dэ = 4z0, приравняв (6.11) и (6.12), легко найти выражение для расчета коэффициента гидравлического тре-

ния = 96/Re, справедливого для ламинарного течения.

6.7 Ламинарное течение в плоском клиновидном зазоре

Решение этой задачи иллюстрирует возникновение поддерживающей силы в подшипниках скольжения при наличии смазывающего слоя жидкости.

Пусть нижняя пластина (рис. 6.4) движется со скоростью и0 в направлении отрицательной оси х, а давление слева и справа от неподвижной пластины равно р0.

	y	p – p0	= f(x)
		p – p0	= f(x)
		l
		P
			1
0
0
			x
u0		x
Рисунок 6.4 – Течение в плоском клиновидном зазоре

При малой величине зазора 0 и высокой вязкости жидкости (т. е. при Re = 2u0 0/ 1) в уравнении движения в проекции на ось х (3.11) можно (см. рис. 6.4) пренебречь инерционными членами и принять dux/dt = 0. Кроме того, поскольку ux/ y ux/ x и fx = 0, то его можно записать в виде (6.9). В тонком слое величина др/дх не зависит от y. Проинтегрируем дважды уравнение

(6.9) по y:

u		1	p y2 C		x y C	x
u	x		p y2 C		x y C	x
	x	2 x		1	2
		2 x
				56

vk.com/club152685050 | vk.com/id446425943

Если ввести параметр клиновидного слоя k = ( 1 – 0)/l ( 1 – зазор при x = l), то толщину зазора можно выразить в виде

1 0 x

kx .

(6.13)

Тогда при граничных условиях их = – и0

при y = 0; их = 0 при y = бу-

дем иметь

1 p

y y

u0 1

(6.14)

2 x

Поскольку иу = 0, то при интегрировании уравнения неразрывности

(2.16) по y получим

dy 0 ,

(6.15)

Так как uy = 0 при y = 0 и при y = , то

Первое же слагаемое (6.15) в условиях данной задачи можно записать в

виде

dy .

С учетом найденных соотношений уравнение (6.15) после подстановки в

него (6.14) и интегрирования дает

1 p

0 ,

12 x

т. е. выражение в скобках есть некоторая постоянная С'/2.

Тогда

u0 C'

(6.16)

Поскольку др/дх = (др/д )/(d /dx), то с учетом (6.13)

p k p

и уравнение (6.16) примет вид

vk.com/club152685050 | vk.com/id446425943

p	6 u		C'
		0			.	(6.17)
		2		3
	k

Проинтегрировав (6.17) по , получим

	6	u	C
р		0			C .
	k		2	2

Постоянные интегрирования С и С" найдем из граничных условий: р = р0 при х = 0 и при х = l. После преобразований окончательно получим


	6 u								1 kl
p p	6 u	1				1			1 kl			0	1
	0											0				.	(6.18)
																.	(6.18)
0	k 0	1	kx				kx	2		kl			2	kl
			kx					2		kl				kl
								2
					1
				0			0				0				0

Расчеты по этой зависимости показывают, что на всей длине l p > p0. Эпюра избыточных давлений приведена на рисунке 6.4. Уравнение (6.18) позволяет вычислить величину поддерживающей силы.

6.8 Ламинарное течение жидкости в зазоре подшипника скольжения

Данная задача (см. рис. 6.5) имеет большое практическое значение и составляет предмет гидродинамической теории смазки, основоположниками которой являются Н.П. Петров, Н.Е. Жуковский и др. [2 – 5].

	e

	R
	R
y	F	R
	F	R
h

Рисунок 6.5 – Течение жидкости в зазоре подшипника скольжения

Врезультате решения этой задачи можно рассчитать:

распределение давления в зазоре подшипника скольжения, заполненного вязкой жидкостью – смазкой;

поддерживающую силу подшипника;

крутящий момент.

vk.com/club152685050 | vk.com/id446425943

Поскольку величина зазора h << R, то решение задачи было выполнено в декартовой системе координат. Ось х направлена по окружности вала в сторону вращения так, что x = R, а dx = Rd , ось y – по нормали к поверхности вала и ось z параллельно оси вала по его поверхности. Поскольку было принято uz = 0, то задачу можно считать плоской. Схема решаемой задачи приведена на рисунке 6.6.

При решении этой задачи были приняты те же допущения, что и при решении задачи о клиновидном зазоре (см. п. 6.7). Поэтому система уравнений

(2.16) и (3.11) примет вид:

дp

;

д 2

R д

(6.19)

1 дu

дu

R д

где = y – R; u = ux.
h = (1 – сos )		y
u	uy		= y – R
		0	= y – R
		0
	R		–
	R
Рисунок 6.6 – Схема течения в подшипнике
		скольжения

Величина зазора в задаче переменна, она зависит от разности радиусов наружного R и внутреннего R цилиндров ( = R – R) и величины эксцентриситета e. Если обозначить относительный эксцентриситет = е/ , то нетрудно найти связь локального зазора h и угла :

h (1 cos ) .

Решение задачи при граничных условиях:

u = 0 при y = 0; u = R при y = h; p =-π = p =

Поддерживающая сила подшипника, приведенная направление действия которой показано на рисунке 6.5, по формуле

F	12 R3		,
	2 2 2
		1 2

(6.20)

дано в [1 – 6].

к единице его длины, может быть вычислена

(6.21)

а момент сопротивления вращению вала

vk.com/club152685050 | vk.com/id446425943

	4 R3			2 2
M		1
					.	(6.22)
	2 2
			1 2

При < 0,3 возможно возникновение отрыва потока от неподвижного внешнего кольца при нагрузке на подшипник, равной G. Для предотвращения этого явления необходимо выполнение условия

G 2	.	(6.23)
R3

6.9 Ламинарное течение в круглой трубе

При установившемся течении жидкости вдоль оси х в горизонтальной трубе uz = uy = 0; Fx = Fy = 0; dux/dt = 0, Fz = – g. Уравнение (3.11) в проекции на оси х, у, z примет вид

1 p

2ux

;

(6.24)

0 g

p .

Из второго уравнения (6.24) следует, что р не является функцией у, а из

третьего – р = С(х) – gz. Таким образом др/дх не зависит от у и z.

При переходе к цилиндрическим координатам (см. рис. 6.7 и приложение

Рисунок 6.7 – Схема перехода в цилиндрическую систему координат

В) с учетом того, что ur = 0 и u = 0 получим

p	2		1	ux
		u2x			.	(6.25)
x			r r
	r

Уравнение (6.25) можно представить так:

vk.com/club152685050 | vk.com/id446425943

1		u		1 p
	r		x		.	(6.26)

r r		r		x

Поскольку производная др/дх не зависит от у и z, r. Проинтегрируем (6.26) дважды по r при граничныхux/ r = 0; при r = r0 ux = 0. Получим

ux 1 p r02 r2 .

4 x

При r = 0

ux umax 1 p r02 .

4 x

то она не зависит и от условиях: при r = 0

(6.27)

(6.28)

Расход жидкости вычислим с учетом (6.27) и (2.5), приняв dSn=2 rdr.

Получим
Q				r4			p
					0					.				(6.28)
					8 x					.				(6.28)
Средняя расходная скорость
υ			Q					r2		p
								0			.			(6.29)
			Sn					8 x			.			(6.29)
			Sn					8 x
Разделив (6.28) на (6.29), найдем umax/υ =2, a (6.27) на (6.29) – профиль
скоростей в безразмерном виде:
	ux					2
	ux	2			1				r					(6.30)
	υ	2			1				2					(6.30)
	υ								r0
Проинтегрируем (6.29) по х, получим
p p p							8 υl					32 υl	,	(6.31)
p p p												d 2	,	(6.31)
1					2				r2			d 2
						0

где d – диаметр трубопровода; p1 и p2 – давления в начале и конце трубопровода.

Сопоставляя (6.31) и (6.7) получим С = 32.

Для расчета потерь давления в трубах нередко применяется формула Дар- си-Вейсбаха (6.12). Приравняв (6.12) и (6.31), получим выражение для расчета коэффициента гидравлического трения:

64	64	(6.32)
υd	Re

6.10 Турбулентное безнапорное течение Куэтта

vk.com/club152685050 | vk.com/id446425943

Наличие пульсационного перемешивания жидкости приводит к выравниванию скоростей в средней части потока. Профиль скоростей в канале приведен на рисунке 6.8.

Для нахождения аналитических выражений для профиля скоростей делаются упрощающие задачу допущения. Поток представляется в виде:

ла мина р но го пр и ст ен ного слоя толщиной , в котором предпола-

гается отсутствие турбулентности, и т ур бу лент но го я др а , в котором вязкость жидкости = 0.

	z, м
0	z0		u00	u
				u


		υ		х, м
		υ
Рисунок 6.8 – Профиль скоростей в канале
Куэтта при турбулентном режиме течения

Если > , то каналы называются гидравлически гладкими, если < , то каналы – гидравлически шероховатые, где – высота микронеровностей на поверхности канала (см. рис. 6.9).



гидравлически гладкий канал

гидравлически шероховатый канал

Рисунок 6.9 – К определению гидравлически гладкого и шероховатого канала

vk.com/club152685050 | vk.com/id446425943

При установившемся течении в канале Куэтта (см. рис. 6.8) уравнение (6.3) существенно упрощается, так как течение равномерное и параметры те-

чения вдоль			оси х не могут изменяться, т.е. dux/dt = 0, fx = 0;
			x 0. Далее, поскольку рассматриваемое течение плоское, то
x uxux

uy = 0 и

xy uxuy y 0 . Поэтому уравнение (6.3) можно записать в

виде

uxuz

или

C1 .

(6.33)

uxuz

Поскольку при z = 0 = 0 ( 0 – касательное напряжение на стенках ка-

C1 = 0.

нала), а uxuz 0 (турбулентность отсутствует), то в (6.33)

Найдем аналитические выражения для профиля скоростей:

а) Профиль скоростей в ламинарном слое. Поскольку в нем отсутст-

0 , то уравнение (6.33) упрощается:

вует турбулентность, т. е. uxuz

ux C1 .z

Проинтегрировав его при граничном условии: при z = 0, ux 0 , получим распределение скоростей в пристенном слое

u			0 z
u	x
	x

или с учетом (6.37):
	ux			u* z	(6.34)
	u				(6.34)
	u
		*

б) Профиль скоростей в турбулентном ядре потока. Приняв в (6.33) = 0, т. е. предположив, что вязкостные напряжения в потоке малы по сравнению


		, получим
с турбулентными турб uxuz		, получим

			C1 0	турб .
	uxuz		C1 0	турб .

Хотя уравнение Рейнольдса в условиях данной задачи существенно упростилось, но для решения его необходимо иметь одну дополнительную зависи-

мость, связывающую турбулентное напряжение турб с уже имеющимися параметрами течения.

vk.com/club152685050 | vk.com/id446425943

Рассмотрим модель Прандтля, устанавливающую такую связь.

С этой целью вводится понятие турбулентная вязкость т и зависи-

мость
				dux	.	(6.35)
	турб		т		.	(6.35)
	турб		т	dz
				dz
По аналогии с вязкостью газа принято
		т lu*				(6.36)

где l – длина пути перемешивания, т. е. пути, при прохождении которого жидкостная частица теряет индивидуальность, смешиваясь с остальным пото-

	0,5
	0,5
ком; u uxuz	– среднее значение пульсационной скорости. Этот пара-
метр обычно называется динамической скоростью.

		0	турб			, то
Поскольку в ядре потока uxuz		0	турб			, то
		u		0	.	(6.37)
		u			.	(6.37)
		*

Прандтль принял
		l z ,				(6.38)

где – коэффициент пропорциональности, < 1. Подставив выражения (6.36)

– (6.38) в (6.35), с учетом равенства турб = 0

последнее примет вид

dux

После интегрирования получим

ln z C .

(6.39)

Постоянную С найдем из условия равенства скоростей на границе лами-

нарного слоя и ядра потока, т. е. приравняв (6.34) и (6.39) при z = :

ln .

(6.40)

Подставим (6.40) в (6.39) и, опуская индекс «х» при скорости, получим:

(6.41)

в котором

vk.com/club152685050 | vk.com/id446425943

ln	z	ln	u*	ln	u* z	.

Точные измерения профиля осредненных скоростей в потоке и напряжений на стенке позволили найти = 0,4; u / = 11,6. С учетом этого (6.41) можно привести к виду

			u* z	.
	u	5,5 2,5ln			(6.42)

u
*

Профиль скоростей, описываемый уравнениями (6.34) и (6.42), называется универсальным (рис. 6.10). Поскольку скорость в турбулентном потоке существенно возрастает лишь вблизи стенки, то уравнения (6.34) и (6.42) остают-

ся приближенно верными и при отсутствии равенства xz = const.

u
u*				3
30
				2
25
20
15	11,6
	11,6
10	1	4
5,5	1	4
5,5
5
0	1	2	3	4 lg u* z
		lg 11,6

Линии 1 – 3 соответствуют уравнениям: (6.34), (6.42), (6.68). Линия 4 – экспериментальные данные

Рисунок 6.10 – Универсальный профиль скоростей

6.11Сопротивление гидравлически гладких труб при турбулентном режиме течения жидкости

Для расчета падения давления по длине горизонтальной трубы применяется уравнение (6.12) Дарси-Вейсбаха, в котором неизвестным пока остается коэффициент гидравлического трения .

Предварительно по (2.5), приняв dS = 2 rdr, с учетом (6.34) и (6.42) и соотношения r=r0 – z (см. рис. 6.5) вычислим среднюю расходную скорость:

vk.com/club152685050 | vk.com/id446425943

	Q	1	r0		2u*

υ			0 u 2 rdr
υ	r02	r02	0 u 2 rdr	u* r0		2

u*r0

0 u*

u* r0 u* z d u* z .



После вычислений и некоторых упрощений (отброшены малые слагаемые) получим

				υ	1,75 2,5ln										u* r0	.		(6.43)
					1,75 2,5ln											.		(6.43)
			u
		*
Установим связь 0		и перепада давлений р. Из условия равновесия сил,
действующих на жидкость в трубе (рис. 6.11) в проекции на ось x, найдем
			r2			p p							2 r l				0
		0						1				2	0				0
или с учетом (6.12)
											r0	p υ2 .						(6.44)
							0					p υ2 .						(6.44)
							0			2l			8
										2l			8


		z


									l
											0
											0
	p1																	p2



														υ

																			x






											0

Рисунок 6.11 – Схема сил, действующих на жидкость

Подставим (6.44) в (6.37), а полученное выражение в (6.43). После преобразований получим расчетную формулу

1	2lg Re	0,8 .
			(6.45)

Уравнение (6.45) можно аппроксимировать более удобным для практических расчетов выражением (уравнение Блаузиуса)

0,316	.	(6.46)

Re0,25

По определению гидравлически гладкие трубы характеризуются неравенством или

vk.com/club152685050 | vk.com/id446425943

u u 11,6.

Подставив в это неравенство уравнение (6.37), с учетом (6.44) получим


Re			11,6
d	8
или приближенное соотношение
Re 20	d	,	(6.47)
Re 20		,	(6.47)

которое определяет условия гладкости стенок труб, а, следовательно, правомерность применения (6.45) или (6.46).

6.12Сопротивление гидравлически шероховатых труб при турбулентном режиме течения жидкости

Гидравлически шероховатые трубы характеризуются неравенством > или u / > 11,6, которое после преобразований можно представить в виде

Re 500	d	.	(6.48)

При выводе уравнения для расчета λ предполагается, что в ядре потока справедливо уравнение (6.39), но постоянная интегрирования С находится из

условия – при z = u 11,6u , т.е.

2,5ln

Вычислим среднюю скорость. Получим

2,5ln

или с учетом (6.37) и (6.44)

С 2,5ln

Это выражение после экспериментального уточнения коэффициента С3 хо-

рошо аппроксимируется более простым (формула Шифринсона):

0,25

0,11

(6.49)

которое применимо при выполнении условия (6.48).

vk.com/club152685050 | vk.com/id446425943

Расчетное уравнение, обобщающее (6.46) и (6.49), т. е. справедливое при турбулентном режиме течения жидкости в трубах (уравнение А. Д. Альтшуля) имеет вид

	68 0,25
0,11		.	(6.50)

d	Re

На рисунке 6.12 приведена зависимость λ от Re и /d в областях ламинарного (линия 1) и турбулентного (линии 2 и 3) режимов течения (диаграмма

Никурадзе).


	0,3
	0,2
		=64/Re
	0,1
	0,08	1
	0,06	1
	0,06
	0,04	3
	0,03	3
	0,03	2
		2
	0,02	=0,316/Re0,25
		=0,316/Re0,25

0,01
102	2	4	6	8	2	4	6	8	2	4	6	8			2	4	6	8
102				103				104	2	4	6	8	10	5	2	4	6	8	Re
													10

1 – гладкие и гидравлически шероховатые трубы 2 – гладкие трубы; 3 – гидравлически шероховатые трубы

Рисунок 6.12 – Зависимость от критерия Re (диаграмма Никурадзе)

6.13 Ламинарное обтекание шара (задача Стокса) |

Течение со столь малыми скоростями, при которых в уравнении НавьеСтокса можно пренебречь инерционными слагаемыми по сравнению с трением, называется ползущим.

При ползущем движении шара относительно вязкой жидкости уравнения (3.12) примут вид (при F = 0):

1	grad p 2u .	(6.51)

Уравнение (6.51) следует решать совместно с уравнением неразрывности (2.16) при граничных условиях:

на поверхности шара u = 0 (условие прилипания), на бесконечном удалении от шара u = U, p = p0.

Задачу обтекания шара следует решать в сферической системе координат. В силу очевидной симметрии полей скоростей и давлений относительно оси х (см. рис. 6.13 и приложение В) математическое описание примет вид:

vk.com/club152685050 | vk.com/id446425943

1 2u

2 u

ctg u

r r

1 p

1 2u

2 u

ctg u

r r

2ur

u ctg

граничные условия:

при

r = a

2 u

2ctg

;

2 u

;

(6.52)

sin

= u = 0;

при r = ur = Ucos ; u = – Usin , p = p0.

Рисунок 6.13 – Схема к расчету силы сопротивления при обтекании шара

После интегрирования [2] найдем:

ur Ucos 1

cos ;

2 r

3 a

1 a

u Usinθ

sin ;

(6.53)

4 r

p p

cos .

На основе соотношений (3.5), записанных в сферических координатах (см. приложение В), с учетом (6.53) можно вычислить нормальную и касательную составляющие напряжения на поверхности шара:

		p 2 ur					3	U cos ;
	r
					r	2		a

			1	ur	u	u			3	U sin .
r ,

	r				r	r			2	a

vk.com/club152685050 | vk.com/id446425943

Величина равнодействующей силы (направленной, очевидно, вдоль оси х) может быть определена по формуле

P r cos r , sin dS 2 Ua 4 Ua

или

P 6 Ua .

(6.54)

Формула (6.50) называется «формулой Стокса». Она определяет силу сопротивления, возникающую при обтекании шара вязким потоком жидкости при ламинарном течении. Поскольку d = 2a, то формула справедлива при условии:

Re Ud 1

Из решения видно, что 1/3 полной силы связана с силами давления, а 2/3

–с силами трения.

Вприкладной гидромеханике для расчета силы сопротивления при обтекании тел любой формы принята формула

P C	S		U 2
		м	(6.55)
x			2

где Сх – коэффициент сопротивления; Sм – площадь миделевого сечения, т. е. проекции тела на плоскость, перпендикулярную к направлению относительного движения тела и жидкости.

Приравняв (6.54) и (6.55), нетрудно найти, что при ламинарном обтекании шара (Sм = а2)

Cx Re24 .

При переходе к турбулентному режиму обтекания влияние числа Re вырождается (рис. 6.14). Столь сложный характер рассматриваемой зависимости объясняется изменением соотношения между сопротивлением трения и сопротивлением давления при изменении Re. При очень малых Re обтекание шара происходит практически без отрыва потока от его поверхности. Влияние вязкости распространяется на большое расстояние от поверхности обтекаемого тела, и основную роль играет сопротивление трения. С ростом Re действие вязкости локализуется в пристеночной области, и появляются вихревые образования в кормовой области (cм. рис. 5.4).

Формулы (6.54) и (6.55) позволяет вычислить скорость равномерного осаждения твердых частиц в жидкости. Так, например, при ламинарном осаждении одиночной частицы диаметром d, плотность материала которой ρт, из баланса сил с учетом (6.54) будем иметь

vk.com/club152685050 | vk.com/id446425943

G A P 0 U т gd 2 .

Сх

103

102

1,0

0,1

0,01					103	104	105	106
0,01	0,1	1,0	10	102	103	104	105	106	Re

1 – по формуле Стокса; 2 – экспериментальные данные (кривая Рэлея)

Рисунок 6.14 – Зависимость коэффициента сопротивления шара от критерия Re

6.14 Уравнения пограничного слоя

В теории пограничного слоя применяется упрощенное математическое описание, позволяющее с достаточной для практики точностью решать аналитически различные задачи гидродинамики. Суть ее состоит в следующем.

Принимается, что поток жидкости, взаимодействующий с твердым телом, потенциален за исключением пристенного слоя, в котором жидкость заторможена за счет вязкостных сил трения. Этот слой и называется пограничным

слоем. Малая толщина пограничного слоя позволяет решать задачи о течении в нем жидкости, выбрав координату х вдоль границы обтекаемой поверхности, а у – нормально к ней. Скорость их претерпевает преимущественное изменение вдоль оси у.

Поэтому можно принять

2ux 2ux .y2 x2

На внешней границе пограничного слоя принимают р и их=U подчиняются уравнению Бернулли (5.8) для потенциального потока:

p U 2 C .g 2g

Дифференцируя по х, получим

vk.com/club152685050 | vk.com/id446425943

1 dp

С учетом приведенных допущений уравнение (3.10) в проекции на ось х в

случае плоской задачи и при Fx = 0 примет вид

x u

(6.56)

y y

Система уравнений (6.56) и (2.16), предложенная Прандтлем, в ряде случаев аналитически решаема.

6.15 Интегральное соотношение пограничного слоя

Уравнение (6.56) представим в виде

U u

2ux

(6.57)

Проинтегрируем каждое из слагаемых по толщине слоя по известному

правилу

fdy f

y 0 .

Поскольку при y = 0

их

= иу

= 0, а при y =

ux = U, то будем

иметь

ux U ux

U ux

U 2 2 ;

U ux dy uy U ux

0 0;

U u

dy U

;

u2x dy

где 0 – касательное напряжение на стенке;

;

(6.58)

dy .

(6.59)

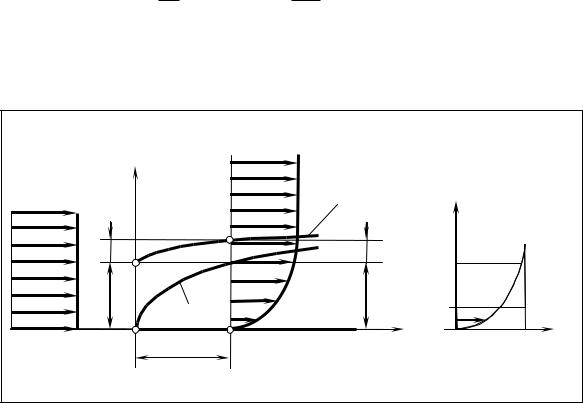
vk.com/club152685050 \| vk.com/id446425943
Интегральное соотношение примет вид
		d	2		dU	0
		dx U		2	U 1 dx	.				(6.60)
Величина 1, определяемая выражением (6.59), называется т олщи-
ной вытеснения. Она определяет, насколько смещаются линии тока ос-
новного потока из-за уменьшения скоростей в пограничном слое (см. рис. 6.15).
					U
	y
U					1			y
			d
1	b					1
	b							δ
								δ
δ		2			ux(y)	δ
		2						1
							x	1		ux
	a	х			c		x		U	ux
	a	х			c				U
1 – граница пограничного слоя; 2 – линия тока
Рисунок 6.15 – Пограничный слой на полубесконечной пластинке

Поскольку расходы через сечения ab и cd должны быть равными, то можно записать

			1
	Udy		ux dy
		0	0
или
		1
Udy ux dy			Udy ux dy U 1
0	0	0	0
Из этого выражения и получается (6.59).
Величина 2, определяемая выражением (6.58), называе т с я толщиной
потери импульса.
Отметим, что скорость их		асимптотически переходит в U, т. е. граница
слоя принимается условно,		например, при их = 0,99U. Толщины же		1 и

2 не зависят от условий назначения , их значения вполне определенны. Проиллюстрируем применение интегрального соотношения при решении

одной из простейших задач.

vk.com/club152685050 | vk.com/id446425943

6.16 Ламинарный пограничный слой на полубесконечной пластине

Задача расчета пограничного слоя сводится к определению силы сопротивления трению Т. При продольном обтекании пластины (см. рис. 6.15) скорость в потенциальном потоке U=const, т. е. U не зависит от х. Поэтому уравнение (6.60) примет вид

		d 2			0		.		(6.61)
		dx			U 2		.		(6.61)
		dx			U 2
Профиль скоростей в пограничном слое может быть представлен в ви-
де
			u	x		y
				x	f			.
			U		f			.
			U
Выбор функции f	произволен, но						f		должна удовлетворять условиям:
при у = 0 их = 0; при	у = ux = U,						ux/ y = 0.

Если принять, что
	u	x	a0 a1	y	a2	y 2
							,
	U

то с учетом приведенных условий найдем					a0 = 0; a1 = 2; a2= – 1, т. е.
	u	x	y	2		y
							.
	U

Подставим (6.62) в (6.58), получим

2 152 .

С учетом (6.62) вычислим


	ux		0 2	U	.
0
	y
		y 0

(6.62)

(6.63)

(6.64)

После подстановки (6.63) и (6.64) в (6.61) получим простое дифференциальное уравнение

d 15U dx ,

интегрирование которого при начальном условии = 0 при x = 0 позволяет найти

30	x	.	(6.65)

	V
74

vk.com/club152685050 \| vk.com/id446425943
Для расчета касательных напряжений принята форма
			C		U 2	(6.66)
	0		C	x	,	(6.66)
	0			x	2
					2
где Сх – локальный коэффициент сопротивления.
Разрешая (6.66) относительно Сх с учетом (6.64), получим
C		x	0,72Re 0,5 ,			(6.67)
		x			x
где Rex = Ux/ – локальное число Рейнольдса.
Полную силу трения Т при двухстороннем обтекании пластины длиной
l и шириной В можно вычислить по формуле
					l
T 2B 0dx .
					0
6.17 Турбулентный пограничный слой на полубесконечной
пластине
Так же, как и при течении в трубах, ламинарный пограничный слой при
достижении критической толщины теряет устойчивость, т. е. при Rex > Rex кр
пограничный слой становится турбулентным, причем Rex кр = 3 105 (см. рис.
6.16).
Ламинарный				Переходная		Турбулентный
пограничный				область		пограничный
слой						слой
						y
						0,99U
y
U						uх
U
					кр
0,99U					кр
0,99U
ux						uл
u						uл
u
						u
хкр						л
хкр

Рисунок 6.16 – Турбулентный пограничный слой
на полубесконечной пластине
Интегральное соотношение (6.60) оказывается верным и для турбулент-
ного пограничного слоя. Это можно получить на основе преобразований урав-
нения Рейнольдса (6.3).

vk.com/club152685050 | vk.com/id446425943

Решим задачу для полубесконечной пластины, полагая, что в пограничном слое справедлив универсальный профиль скоростей, определяемый уравнениями (6.34) и (6.42).

При этом с целью облегчения дальнейших выкладок целесообразно уравнение (6.42) аппроксимировать степенным одночленом (см. рис. 6.10)

				u y 1 7
	u	x	8,74
					*	(6.68)

u*

и, так как		x = U при y = , то
и, так как	u	x = U при y = , то
													y		1 7
								u		x			y		1 7
										x					.				(6.69)
															.				(6.69)
							U
По уравнению (6.58) с учетом (6.69) найдем
												7		.					(6.70)
									2			72		.					(6.70)
									2

Подставив (6.37) в (6.68), можно получить
			0															0,25
							0,0225											.	(6.71)
						2	0,0225											.	(6.71)
			U												U
Проинтегрируем (6.61), предварительно подставив в него (6.70) и (6.71).
При начальном условии = 0 при x = 0 получим
													1 5			4 5
		0,37													x		.		(6.72)
		0,37													x		.		(6.72)
											U
Из (6.66) с учетом (6.71) и (6.72) найдем
		C		x	0,058Re 0,2 .														(6.73)
				x											x

Далее можно вычислить силу трения, действующую на пластину.

6.18 Струйное течение

Применение уравнений пограничного слоя необязательно связано с наличием взаимодействия жидкости с твердыми стенками. Они могут быть применены в случае, когда внутри потока имеется слой жидкости, в котором преобладающую роль играют силы трения. Примером такого течения является ламинарное течение затопленной струи (рис. 6.17). Уравнения пограничного слоя, записанные в цилиндрических координатах (см. приложение В) с учетом того, что давление во всем объеме жидкости постоянно, примут вид:

x ur

;

r r

vk.com/club152685050 | vk.com/id446425943

ux ur ur 0,

x r r

а граничные условия: при r = 0

u 0; ux 0,

r	r

а при r ux = 0.

u(x, y)

Рисунок 6.17 – Картина линий тока в

ламинарной круглой затопленной струе

Теоретически найденное поле осевых скоростей [1] описывается уравне-

нием
u	3 J		3 J		r	2 2
	3 J	1	3 J		r		,	(6.74)

			64	2	x	2
	8 x		64		x

где J 2 r ux2dr – поток импульса, который постоянен в направлении оси х

и равен начальному J0 = u02S0; S0 – площадь поперечного сечения отверстия; и0 – скорость жидкости в отверстии.

Из анализа (6.70) видно, что с удалением от отверстия скорость в струе уменьшается. При этом, однако, количество увлекаемой в движение жидкости увеличивается, струя расширяется и расход жидкости

Q ux 2 rdr 8 x

прямо пропорционален х.

vk.com/club152685050 | vk.com/id446425943

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Как соотносятся максимальная и средняя скорости при равномерном ламинарном движении в цилиндрической трубе?

2 Как распределяются касательные напряжения по сечению цилиндрической трубы при равномерном движении?

3 От каких величин зависит коэффициент Дарси при равномерном ламинарном движении?

4Поясните понятия «гидравлически гладкий» и «гидравлически шероховатый» канал.

5Как рассчитывается толщина вязкого подслоя? В зависимости от каких других величин может изменяться толщина вязкого подслоя?

6Какие зоны сопротивления при равномерном турбулентном движении в трубах можно указать?

7Физический смысл числа Re? Что характеризует критическое число Re?

8Какова связь между средней и динамической скоростями потока?

9Каков физический смысл чисел подобия?

10 Каковы основные достоинства теории подобия?

11 Каковы основные особенности механизма движения жидкости при ламинарном и турбулентном режимах?

12 Что характеризует динамическая скорость потока и посредством каких параметров она определяется?

13 Почему одна и та же труба может быть в одном случае гидравлически гладкой, а в другом – гидравлически шероховатой?

14 В чем заключаются условия подобия двух явлений?

15 Как вычислить число Рейнольдса для некруглой трубы?

16 Каковы границы зон сопротивления при турбулентном течении?

17 Что собой представляет модель Прандтля?

18 Что собой представляет универсальный закон распределения скорости?

19 Как соотносятся между собой силы давления и вязкого трения при обтекании шара?

20 Каким образом определяется сила сопротивления при обтекании шара? 21 От чего зависит коэффициент сопротивления при обтекании шара?

22 Каковы особенности течения вязкой несжимаемой жидкости клиновидном зазоре?

23 Каковы причины возникновения поддерживающей силы в подшипнике скольжения?

24 Что называется пограничным слоем? Каковы его особенности? 25 Физический смысл толщины вытеснения?

26 Посредством, каких величин определяются касательные напряжения при обтекании полу бесконечной пластины?

vk.com/club152685050 \| vk.com/id446425943
7 ОДНОМЕРНЫЕ ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
В прикладной гидромеханике одномерными обычно называют потоки, в
которых гидродинамические величины (скорость, давление) зависят только от
одной геометрической координаты. Если реальные потоки жидкости в каналах
различной формы характеризовать средней расходной скоростью и давлением
на оси потока, то такой поток можно считать одномерным.
7.1. Уравнение Бернулли для потока вязкой жидкости
Применим уравнение энергии в интегральной форме (3.14) – (3.18) к объ-
ему движущейся жидкости, ограниченному стенками канала Sст и двумя живы-
ми сечениями S1 и S2. Последние расположены в тех местах, где линии тока па-
раллельны, т. е. живые сечения плоские, причем жидкость течет от сечения 1 к
сечению 2. (рис. 7.1). Преобразуем последовательно все слагаемые
u du				2			2				2
u du		dV d	u	dV		u		dV		u	un ds .
V	dt	V dt	2		V t	2			S	2
		z				υ2
		z
		z2	S2		2
		z2
					p2	2
				υ1
					Sст
		z1		S1
		p1		S1
		p1
								x
		Рисунок 7.1 – Схема канала
Преобразование 1-ого слагаемого:

	u	2		dl u2dS 0		υ2 S dl 0 Q υ dl
		dV

			2 t
V t	2			l S	2 l t	l t

(υS = Q в момент времени t не зависит от координаты по длине канала).

Преобразование 2-ого слагаемого:

Поскольку S = S1 + S2 + Sст и на стенке un = 0. Тогда

при	S = S1	un= – u	u2un ds u3dS 1υ13s1 1υ12Q ;
			S1	S1
при	S = S2	un = u	u2un ds 2υ22Q
			S2

vk.com/club152685050 | vk.com/id446425943

и при S = Sст un = 0 u2un ds 0.

Sбок

Итак, после простых преобразований найдем:

υ2

dV Q

dl 2

(7.1)

где

u2 dS

;

u3dS

S1, 2

υ Q

1,2

υ2

1, 2

Коэффициенты

и 2 – это отношение действительной кинетической

энергии потока Q к вычисленной по средней скорости (коэффициенты кинети-

ческой энергии).

Коэффициент 0 – это отношение действительного потока количества движения к вычисленной по средней скорости.

Обозначим

cp	dT	dV gQhW .		(7.2)

V	dt

Поскольку выбранные сечения плоские, то напряжение в них рп = – р и
pn u dS pudS pudS .				(7.3)
S	S1		S2
Если течение происходит в поле сил тяжести, то f				g , и можно пока-
зать, что
f u dV gzudS gzudS .				(7.4)
V	S1		S2

Просуммируем выражения (7.3) и (7.4). С учетом того, что в живом плоском сечении давление изменяется по закону статики, то p + ρgz = const и

		p		p
pn u dS f u dV gQ z1		1	z2	2	.	(7.5)
pn u dS f u dV gQ z1		g	z2		.	(7.5)
S	V	g		g

После подстановки (7.1), (7.2) и (7.5) в (3.12) и простейших преобразований получим

	p		υ2		0	υ	p		υ2
	1	1			0	t dl z2	2	2
z1		1						2		hw .	(7.6)
z1	g	1	2g	g			g	2	2g	hw .	(7.6)
						l

1 к 2 необходимо сообщить ей

vk.com/club152685050 | vk.com/id446425943

Уравнение (7.6) представляет собой баланс энергий. Слагаемое hw – удельная механической энергии перешедшая в теплоту за счет трения внутри жидкости (диссипация энергии), или гидравлические потери. При известном поле скоростей в канале с учетом уравнений (3.20) и (3.21) гидравлические потери можно вычислить по формуле

hw gQ V DdV

Гидравлические потери условно разделяются на два вида.

1 – Гидравлические потери по длине hl. Эти потери возникают в прямых каналах постоянного сечения и пропорциональны длине канала.

2 – Гидравлические потери на местных сопротивлениях hм. Эти поте-

ри возникают в местах изменения сечения канала или искривлениях его оси, т.е. в местах перестройки поля скоростей. Примеры местных сопротивлений: вентиль, кран, расширение, сужение, поворот канала и пр.

При известных эпюрах скоростей в сечении канала всегда можно вычислить коэффициенты 0, 1 и 2.Так при ламинарном течении в круглых трубах с учетом (6.30) найдем 1, 2 = 2 α0=1,33, а при турбулентном, когда эпюра скоростей приближается к прямоугольной, можно принять 0 = 1, 2 = 1.

В случае установившегося движения жидкости, когда Q = const иυ/ t=0 уравнение Бернулли принимает вид:

υ2

h .

(7.7)

2 2g

1 2g

7.2 Уравнение Бернулли для сети с насосом

Если выполняется условие

z	p		υ2	z		p		υ2
	1		1			2		2	,
	g					g	2 2g
1		1 2g			2

то для обеспечения подачи жидкости от сечения энергию внешним источником, или насосом.

Удельная энергия, сообщаемая жидкости насосом, называется полезным напором и обозначается Н, [H] = м. Уравнение баланса энергий в этом случае имеет вид

H z

υ2

h .

(7.8)

2 2g

1 2g

Это уравнение позволяет для заданной схемы трубопроводов рассчитывать Н, и, следовательно, подобрать насос. Поскольку слагаемые

vk.com/club152685050 | vk.com/id446425943

		υ22			υ12		h f Q ,
	2 2g
				1 2g			w
то уравнение (7.8) можно записать так:
H z				z		p2 p1		f Q .	(7.9)
			2
				1			g

Эта зависимость называется характеристикой сети.

7.3 Гидравлические потери по длине

Составим уравнение Бернулли (7.7) для горизонтального участка трубы (см. рис. 6.11). В этом случае z1 = z2 = 0; υ1 = υ2 = 0. Из (7.7) получим

hl = (p1 – p2)/( g)

или с учетом (6.12)
h	l		υ2		.	(7.10)

l	d 2g

Отметим, что (7.10) можно получить из (7.2) с учетом (3.21) и (6.30).
7.4 Гидравлические потери на местных сопротивлениях
Для расчета их используется формула Вейсбаха
h		υ2		,		(7.11)

м		2g

где – коэффициент местного сопротивления, обычно определяемый опытным путем. Общий вид зависимости ζ(Re) приведен на рис.7.2.

= кв + С/Reкв

кв

Рисунок 7.2 – Вид зависимости коэффициента местного сопротивления от числа Re

При ламинарном режиме гидравлические потери пропорциональны скорости в первой степени, т.е. ζ = С/Re. При турбулентном режиме ζ = кв = const и гидравлические потери пропорциональны скорости в квадрате.

vk.com/club152685050 | vk.com/id446425943

Рассмотрим несколько примеров расчета местных гидравлических по-

терь.

а) Гидравлические потери при внезапном расширении (рис. 7.3)

можно найти аналитически. Рассмотрим решение этой задачи подробно (в гидравлике она получила название «Теорема Борда»).

К жидкости, находящейся в момент t в объеме V1–2 между сечений 1 – 1 и 2 – 2, применим 2-ой закон Ньютона (3.2). В проекции на ось х

dkx

(7.12)

где

kx , t udV ;

Rmx

V1 2

fx 0;

V1 2

RSx p1S2 p2 S2 .

υ2

υ1

р2

р1

dx1

dx2

Рисунок 7.3 – Схема к расчету гидравлических потерь при

внезапном расширении

kx , t udV ; Rmx V1 2

V1 2

(7.13)

RSx p1S2 p2 S2 .

За время dt жидкость сместится (сечение

1 – 1, а именно а – а,

в 1' –

1', сечение 2—2 в 2' – 2') и займет объем V1 –2 . Изменение количества движе-

ния составит

dkx kx , t dt kx , t

udV udV udV udV .

(7.14)

V1 2

V1 1

V2 2

Предположив, что в выбранных сечениях эпюра скоростей прямоуголь-

ная, (u = υ1 и u = υ2) получим V1–1 = S1dx1; V2–2

= S2dx2. С учетом того, что

dx1 = υ1dt; dx2 = υ2dt; Q = υ1S1 = υ2S2, уравнение (7.14) можно привести к виду

vk.com/club152685050 | vk.com/id446425943

dkx	υ22 S2 υ12 S1 S2 υ22	υ1υ2 .	(7.15)

dt

Подставим (7.15) и (7.13) в (7.12), найдем

p p	υ2	υ υ
1 2	2	1 2	.	(7.16)
g
		g

Для нахождения гидравлических потерь применим уравнение Бернулли (7.7) для сечений 1 и 2. Поскольку z1 = z2 = = 0, то

h	p p	υ2	υ2
	1 2	1 1	2 2 .	(7.17)
			2 2 .	(7.17)
w	g		2g
	g		2g

В условиях, когда в сечении u = υ; = 1 с учетом (7.16), получим уравнение Борда для расчета гидравлических потерь hв.р при внезапном расширении потока:

hw hв.р	υ	υ	2
	1	2	.	(7.18)
		2g	.	(7.18)
		2g

Учитывая, что υ1S1 = υ2S2, представим (7.18) в виде (7.11)

		υ2		υ2
h		1		2	,
			2 2g
в.р	1 2g

где 1 = (S1/S2 – 1)2; 2 = (1 – S2/S1)2.

Выполненный анализ позволил установить, что коэффициент местного сопротивления зависит только от соотношения геометрических размеров местного сопротивления. Однако этот вывод справедлив лишь при развитом турбулентном течении, когда профиль скоростей близок к прямоугольному.

б) Гидравлические потери при внезапном сужении канала (рис.7.4).
	С
υ1; S1	υС; SC	υ2; S2	x
			x
	С

Рисунок 7.4 – Схема к расчету гидравлических потерь при внезапном сужении

При выполнении анализа конкретного вида местного сопротивления необходимо представить себе картину течения, т.е. вид линий тока. На рисунке 7.4 показаны линии тока, которые охватывают практически весь поток. Нетрудно представить, что из-за действия сил инерции сжатие потока про-

vk.com/club152685050 | vk.com/id446425943

должится вплоть до сечения С-С, а далее произойдет расширение потока. Картина расширения напоминает внезапное расширение. Отметим, что основная доля теряемой механической энергии происходит именно при расширении потока. В соответствии с таким представлением потока можно с учетом (7.11) найти

υ2

υC

υ2

(7.19)

в.с 2g

в.с

сж 2g

где

в.с

сж2

1 ;

(7.20)

= SC/S2 – коэффициент сжатия потока.

Вывод уравнения (7.20) выполнен с учетом соотношения (2.17) Q = υCSC = υ2S2, из которого следует, что υC = υ2/ε.

Экспериментально найдено, что ζсж = 0,05 и

0,62 0,38	SC	2	(7.21)

	S2

При выполнении практических расчетов применяется более удобная зависимость

в.с	0,5		S1
		1		,	(7.22)
			S2

которая дает близкие к (7.20) результаты.

в) Гидравлические потери при входе жидкости из резервуара в трубу

(рис.7.5). Это случай внезапного сужения, при S1 = вх = в.с = 0,5.

Рисунок 7.5 – Вход в трубу

г) Гидравлические потери при выходе жидкости из трубы в резервуар

(рис.7.6). Это случай внезапного расширения при υ2 = 0 вых = 1.

д) Гидравлические потери в диффузоре (рис.7.7). Расчетное уравнение имеет вид:

vk.com/club152685050 \| vk.com/id446425943
hдиф D hв.р. ,
где φD – коэффициент диффузора, величина которого зависит от угла рас-
крытия β усеченного конуса: при = 0	φD = 0, при = π φD = 1.
	S1	S2
	S1
		υ1	υ2
Рисунок 7.6 – Выход из трубы в	Рисунок 7.7 – Диффузор
резервуар	Рисунок 7.7 – Диффузор
резервуар

7.5 Приборы для измерения скоростей и расходов

Здесь мы рассмотрим только те приборы, принцип действия которых может быть объяснен с помощью уравнения Бернулли.

а) Трубка Пито (рис. 7.8).

1	2
h	2
h1	h2
u
p
Рисунок 7.8 – Трубка Пито

В пьезометрической трубке 1, или трубке статического напора,

уровень жидкости h1 = p/( g). При обтекании устья трубки полного напора

2 происходит торможение потока, т. е. преобразование кинетической энергии в энергию давления , и

h1 = p/( g) + u2 /(2g).

Перепад уровней

h = h2 – h1 = u2/(2g),

т. е. прибор позволяет измери ть локальную скорость в кан але: u 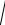2gh

vk.com/club152685050 | vk.com/id446425943

б) Плоский зонд (рис. 7.9) применяется для измерения величины и направления локальной скорости в плоском потоке. Измерив перепады уровней h2 – h1 и h2 – h3 , каждый из которых зависит от значения скорости и и угла набегания потока, получаем возможность нахождения и и ;

u	h1	h2
		h2	h3
			h3
	1

	2
	3
Рисунок 7.9 – Плоский зонд

в) Шаровой зонд – это шарик, в теле которого выполнено пять каналов: три – как показано на рис. 7.9, у плоского зонда и еще два – смещенных относительно канала 2 в горизонтальной плоскости. Применяется для измерения направления и величины локальной скорости в пространственном потоке;

г) расходомер с соплом Вентури. Применим уравнение Бернулли (7.7) к сечениям 1 и 2 (рис. 7.10).

		h
	1
			2
υ1	p1	p2	υ2	S2	S1
	p1	p2	υ2	S2	S1	x
						x
			2
	1
	Рисунок 7.10 – Расходомер Вентури

В данном случае z1 = z2 = 0, p1 – p2 = gh. Подставив эти выражения и уравнение (2.7) в (7.1) и решив его относительно υ1, найдем

υ1		2gh				,

			S1	2
	2		S1		1
	2		S2		1
			S2

где S1 и S 2 – площади сечений трубы и горловины расходомера Вентури.

vk.com/club152685050 | vk.com/id446425943

Расход жидкости вычислим по формуле Q=υ1S1.

д) Расходомер с диафрагмой (рис. 7.11).

		h
	1	2
υ	S0	Sc	S	x
	S0	Sc	S	x
	1	2

Рисунок 7.11 – Расходомер с диафрагмой Установка тонкостенной шайбы вызывает сжатие потока, причем в сече-

нии 2 площадь сечения струи Sc < S0 (S0 – площадь сечения отверстия). Их от-

ношение Sc/S0 = называется коэффициентом сжатия струи. По аналогии с предыдущей задачей найдем

υ		2gh					.

			S1	2
					1
	2					1
			S2		2

е) Ротаметр (рис. 7.12) – это расходомер, выполненный из стеклянной конической трубки, внутри которой находится поплавок. При расходе жидкости Q поплавок устанавливается по высоте а.

Sп

р2

υк

р1 a

Рисунок 7.12 – Ротаметр

Установим вид зависимости Q = f(a). Запишем условие равновесия вертикальных составляющих сил, действующих на поплавок

vk.com/club152685050 | vk.com/id446425943

п gVп ж gVп p1 p2 Sп 0

где Vп – объем поплавка; ρп – плотность материала поплавка; Sп – площадь сечения поплавка.

Поскольку величины двух первых слагаемых не зависят от расхода, то для прибора р1 – p2 = const. Следовательно, гидравлические потери, возникающие при обтекании поплавка,

h	p p	υ2
	1 2	к	.

w	g	2g

Поскольку площадь кольцевого канала

Sк = S – Sп,

то скорость жидкости

υк = Q/(S – Sп) = const.

При выполнении условия S = S0+ka (k – коэффициент пропорциональности) окончательно получим

Q= υк(S0 – Sп + ka).

7.6Истечение жидкости

При истечении жидкости через отверстие или насадки из сосуда под давлением р0 для расчета скоростей и расходов используются зависимости

υ 2gH ;			(7.19)

Q S0 2gH ,			(7.20)

где 2gH υт – некоторая теоретическая скорость, достигаемая при отсутствии гидравлических потерь в жидкости;

φ = υ/υт – коэффициент скорости; µ = Q/Qт – коэффициент расхода;

S0 – площадь сечения отверстия или насадка. Рассмотрим различные случаи истечения.

а) Истечение жидкости через отверстие с острой кромкой. При вы-

ходе жидкости из отверстия (рис. 7.13) наблюдается сжатие струи под действием сил инерции с коэффициентом сжатия = Sc/S0. Составим уравнение Бернулли (7.7) для сечений 1 и 2, где z1 = h; z2 = 0; υ1 = 0; υ2 = υ; hw = hм.c =υ2/(2g). Решим (7.1) относительно υ и сопоставим с (7.19). Найдем, что при

H	p0 p2	h	1	.	(7.21)
	g

vk.com/club152685050 | vk.com/id446425943

p0
1	1
h
	Sc
	2
S0	υc	x
	2

Рисунок 7.13 – Истечение через отверстие с острой кромкой

Поскольку Q = υcSc = υS0 = S0 2gH , то с учетом (7.20) = . При турбулентном режиме истечения, когда 2 = 1, коэффициент местного сопротивления при сжатии потока = 0,05, коэффициент скорости = 0,98 и при экспериментально найденном значении коэффициента сжатия = 0,64 коэф-

фициент расхода = 0,62. При ламинарном режиме коэффициенты , , существенно зависят от числа Рейнольдса, для расчета которого применяется

формула Re = υтd0/ , где d0 – диаметр отверстия, – кинематическая вязкость жидкости. На рисунке 7.14 приведены экспериментальные данные, полученные А.Д. Альтшулем для круглого отверстия в тонкой стенке.

ε, φ, μ
1
0,8	ε			φ
0,8
0,6			μ
			μ
0,4
0,2
0	2	3	4	10	5 Re=υ d	/
10	2	3	4		5 Re=υ d	/
10	10	10	10		т 0
Рисунок 7.14 – Зависимости , и от Re для
круглого отверстия в тонкой стенке

б) Истечение жидкости через цилиндрический насадок. При входе жидкости в патрубок в сечении с-с (рис. 7.15) происходит сжатие струи до величины Sс. Далее следует расширение потока до величины S0.

vk.com/club152685050 \| vk.com/id446425943
		1	p0	1
		1		1
		h
				c	2
			Sc		υc	x
				c	2
					l
			Рисунок 7.15 – Истечение через
			цилиндрический насадок
В уравнении Бернулли, записанном для сечений 1 и 2, z1 = h; z2 = 0;
υ1 = 0; υ2 = υ; hw = hc + hв . р + hl, где гидравлические потери при
сжатии потока h	c	= υ 2/(2g), а при расширении потока с учетом (7.18)
	c	c	c
				υ υ 2
			hв.р	c	2
			hв.р	2g
				2g
Для коротких насадков гидравлическими потерями по длине hl можно
пренебречь. С учетом выше отмеченного и соотношений υсSc = υ2S0; = Sc/S0,
нетрудно найти выражения для расчета υ2					и Q, сопоставив которые с (7.19) и
(7.20), получим

	1				; .



	1 2 1 1 2

Экспериментально найдено, что при турбулентном истече нии µ = 0,80 0,82. Длина патрубков l принимается обычно равной 3 4 диаметра. Это обеспечивает завершение расширения потока внутри насадка. Если составить уравнение Бернулли для сечений с и 2, то при α = 1 найдем

p p	υ2	1	0,
c 2	2
g	2g
g	2g

т. е. рс < р2.

Картина истечения между сечениями 1 и с аналогична картине истечения через отверстие (см. рис. 7.13), но в насадке жидкость истекает в область пониженного давления. Этим объясняется увеличение расхода Q по сравнению с отверстием.

vk.com/club152685050 \| vk.com/id446425943
в) Истечение жидкости через водослив прямоугольного сечения (рис.
7.16) шириной В. Расход в слое dz с учетом (7.20) составит dQ = B(2gzdz)0,5.
Проинтегрировав это выражение по z от 0 до Н, получим после преобразований
Q = mBH1,5(2g)0,5, где m 2/3 – коэффициент расхода водослива; m = 0,45.
	z
H	dz

	Q
Рисунок 7.16 – Перелив жидкости
	через водослив
г) Опорожнение вертикального цилиндрического сосуда (рис. 7.17).
При S << S0 можно считать течение установившимся.
Пусть в момент времени t уровень жидкости равен H. Тогда за dt с уче-
том (7.20) вытечет объем

dV Qdt S0 2gH dt

и уровень жидкости понизится

dH dV	S0	2gH dt .
S	S
S
		p
p0
		H0
H
	S0
Рисунок 7.17 – Слив жидкости из
резервуара

Разделив переменные, проинтегрируем это уравнение при начальном условии Н = Н0 при t = 0. Получим, что время опорожнения сосуда t = 2V0/Q0,

vk.com/club152685050 | vk.com/id446425943

где V0 = sH0; Q0= S0(2gH0)0,5; V0, Н0 – начальные объем и уровень жидкости в сосуде.

7.7 Поле скоростей и давлений в циклонном устройстве

В отличие от ранее рассмотренного относительного покоя (см. рис. 4.7), где вращение внутренним слоям жидкости передавалось за счет сил трения, в циклоне движение центральных слоев происходит за счет перемещения вращательно движущейся жидкости от периферии к центру (рис. 7.18).

Рисунок 7.18 – Циклонное

устройство

Приведем решение задачи при течении идеальной жидкости. При движении жидкости в плоскости ху координата z = const и полный дифференциал уравнения Бернулли (5.9) можно записать в виде

	p	udu
d			(7.22)

Поскольку радиальная составляющая скорости ur << u, то в уравнении движения (5.1) при проектировании его на радиальное направление можно

пренебречь слагаемым		dur/dt. С учетом того, что f		2r , a
		p		r

gradp	r p r получим		r 2r , или, так как в условиях данной

задачи давление зависит только от одной переменной r, то можно перейти к полным дифференциалам и записать

	p	2 rdr	u2
d				dr .	(7.23)

			r

Приравняв (7.22) и (7.23), получим дифференциальное уравнение, интегрирование которого дает

ln r ln u C1 .

С учетом граничного условия (при r=r0 u=u0) получим

ru r0u0 C .

(7.24)

vk.com/club152685050 | vk.com/id446425943

Подставим выражение для и, найденное из (7.24), в (7.23). После интегрирования при начальном условии р=р0 при r=r0 найдем

p p0	u2	r
	0			0
	2
			r

2
2
	1 .	(7.25)
	1 .	(7.25)

На рисунке 7.19 приведены в графической форме распределения скоростей и давлений по радиусу циклонного устройства. Поскольку в реальной жидкости давление не может быть меньше давления насыщенного пара .рн. п, то в центре циклонного устройства возможно образование парового столба.

			r
0	rп. ст	r0	r

p p0

рн.п
					r
				r0
	0
		r	п. ст

Рисунок 7.19 – Распределение скоростей

идавлений в циклонном устройстве

7.8Вторичные токи в реальной жидкости

Вторичными называются течения, возникающие в поперечном сечении каналов из-за наличия вязкости жидкости. В качестве примера рассмотрим течение жидкости в цилиндрическом змеевике (рис. 7.20), выполненном из трубы диаметром d.

υ		r2
	C	r2
	C
d	A	D	r1
2		D
2
	B
υ			D/2
D		υ
D
Рисунок 7.20 – Иллюстрация закономерностей тече-
ния жидкости в змеевике

vk.com/club152685050 | vk.com/id446425943

В центре потока из-за наличия плавного поворота создается центробежное поле давлений и рА > рB. В жидкости, примыкающей к стенке, движение отсутствует, т. е. центробежное поле давлений возникнуть не может. Условие отсутствия движения жидкости в поперечном сечении – это равенство давлений при r = const, т. е. рА = рC и рВ = рD. Однако в реальной жидкости оно невыполнимо, и вблизи стенки возникает движение, направленное к оси змеевика, а в ядре потока – от оси змеевика.

Вторичные токи вызывают деформацию профиля скоростей. Максимум скорости смещается (рис. 7.20). В результате изменяются как сопротивление канала (рис. 7.21), так и характер смены режимов (рис. 7.22).

lg	lg Reкр

= const

Reкр2

lg 2320

Reкр1

Re = 2320

Reкр2

lg Re

1 – для прямых труб; 2 – для змеевика

Рисунок 7.22 – Характер смены

Рисунок 7.21 – Зависимость от Re

режимов

При течении жидкости в змеевике различают:

ламинарный режим течения Re < Reкр1 (область l на рис. 7.21) – это область, где кривизна канала не влияет на его сопротивление.

ламинарный режим с вторичными токами Reк р 2 > Re > Reк р 1 (область ll).

турбулентный режим (область lll) Re > Reк р 2 , в этой области

линии = f(Re) для змеевика и прямого каналов параллельны. Установлено, что вторичные течения не оказывают заметного влияния на

гидравлическое сопротивление при выполнении условия

Re	R	32 ,	(7.26)
	r

и, соответственно,

Reкр1 32rR ,

где R – радиус трубы; r – радиус кривизны трубы.

В этом случае коэффициент гидравлического трения можно вычислить по формуле (6.28). В том случае, когда Reкр1 < Re < Reкр2 коэффициент гидравлического трения можно вычислить по формуле:

vk.com/club152685050 | vk.com/id446425943

18,5Re 0,64	R 0,18	(7.27)


	r

а при Re > Reкр2

	1	0, 075Re	0,25		R 0,5
						,	(7.28)
0
				r

где 0 – коэффициент гидравлического трения при турбулентном режиме течения жидкости в прямой трубе, определяемый по формуле (6.46), а для вычисления Reкр2 можно воспользоваться зависимостью

Reкр2 2 104 R / r 0,33 .

Приведенные формулы можно применять при R/r > 0,005.

Отметим, что зависимость от Re – это гладкая, непрерывная функция (см. рис. 7.21), т.е. кризисные явления отсутствуют, а числа Reкр1 и Reкр2 отражают область применения отдельных формул. Это связано с тем, что вторичные токи переносят импульс поперек потока, т. е. выполняют ту же функцию, что и турбулентные пульсации, а, именно деформируют поле скоростей.

7.9 Гидравлический удар в трубах

Если внезапно остановить движущийся в трубе поток жидкости, то в соответствии с уравнением (3.1) изменение количества движения вызовет возникновение избыточной силы давления жидкости на задвижку (рис. 7.23).

	1	х	0
	1		0
	c
p0	υ0	υ = 0	p
	1 l		0
	1 l
х

Рисунок 7.23 – Схема к расчету гидравлического удара

Очевидно, что абсолютно несжимаемая жидкость вызвала бы бесконечное по величине давление р при мгновенной остановке в недеформируемом трубопроводе. Однако в результате сжимаемости реальных жидкостей остановка жидкости в трубе даже при мгновенном закрытии заслонки происходит во времени. Возникающая при этом волна давления распространяется в среде со скоростью, равной скорости звука с. К моменту времени t она достигнет сечения 1 – 1, отстоящего от заслонки на расстоянии х = ct. Справа от него жидкость будет находиться в покое и давление в ней будет р, а слева – количество

vk.com/club152685050 | vk.com/id446425943

движения жидкости изменится от начального K0 = Slυ0

до K = S(l – x)υ0,

т.е.

K K0

Sxυ0

Sυ c ,

(7.29)

x c

где υ0 – средняя скорость течения жидкости в трубе до остановки; S – площадь сечения трубопровода.

В соответствии со вторым законом Ньютона изменение количества движе-

ния уравновесится силой
F p p0 S pS .	(7.30)
Приравняв (7.29) и (7.30), получим выражение для расчета скачка давле-
ния р, возникающего при гидравлическом ударе:
p cυ0 .	(7.31)

После остановки жидкости во всем объеме трубы начинается процесс послойного расширения. Слева направо идет волна разрежения. Итак, перед заслонкой давление р0 сохраняется в течение времени Т=2l/с. Величина Т назы-

вается фазой прямого удара.

Более детальный анализ гидравлического удара проведем на основании уравнения движения (5.1) и уравнения неразрывности (2.14) идеальной сжимаемой жидкости. Анализ проведем в предположении, что в уравнении динамики можно не учитывать сжимаемость, т. е. считаем относительное изменение плотности жидкости незначительным. В этом случае при течении вдоль оси х в каналах постоянного сечения конвективное ускорение равно 0, т. е.

		du	u .

		dt		t
Поскольку fx = 0, то, полагая ux = υ, уравнение (5.1) в проекции на ось х
примет вид
	υ		p .			(7.32)

	t		x
Уравнение (2.14) для одномерной задачи можно записать так
				υ	.	(7.33)
	t
				x

Если плотность жидкости ρ однозначно определяется давлением (такие жидкости называются баротропными), т. е. ρ = ρ(р), то левую часть в (7.33) можно представить в виде

d p .

t dp t

vk.com/club152685050 | vk.com/id446425943

Производная dρ/dp всегда больше нуля и постоянна. Обозначим dp/dρ=c2. С учетом этого уравнение (7.33) примет вид

c2	υ	p .	(7.34)
	x
		t

Отметим, что для газов p/ρ = RT; при T = const dp/dρ = RT = const. Решим совместно уравнения (7.32) и (7.34).

Продифференцировав (7.32) по t, (7.34) по х и приравняв смешанные вторые производные, найдем

2 υ

(7.35)

По аналогии, взяв соответственно производные по х и t, получим

2 p

(7.36)

Уравнения (7.35) и (7.36) называются в математике волновыми. Они мо-

гут быть проинтегрированы в общем виде введением новых переменных

; t

(7.37)

Решения имеют вид

p p0

f ;

(7.38)

υ υ0

F .

(7.39)

В случае закрытия трубопровода в начальный период имеет место одна

волна и решение (7.38) и (7.39) с учетом (7.37) следует искать в виде

p p0

f t

;

(7.40)

υ υ0

(7.41)

Из (7.40) видно, что р – p0 = const, если t – х/с = const, т. е. если х с течением времени изменяется со скоростью с. Таким образом, с – это скорость распространения ударной волны (скорость звука). Решение (7.40) показывает, что распределение давлений, сформированное по х в момент времени t, отвечающее функции f(0 – х/с), остается по форме неизменным во времени, но целиком смещается вдоль оси х со скоростью с. Подставив (7.40) и (7.41) в выражения (7.32) и (7.34), нетрудно показать, что

vk.com/club152685050 | vk.com/id446425943

F 1c f

Тогда (7.41) примет вид
c υ υ	f	t	x	.	(7.42)
c υ υ	f	t		.	(7.42)
0
			c

Приравняв (7.40) и (7.42), получим p – p0 = ρc(υ – υ0), а при полной остановке жидкости (υ = 0) – уравнение (7.31). Во входном сечении, т. е. при х = l, давление во времени не может измениться и р = p0 = const. Здесь зарожда-

ется отраженная волна . Из (7.38) следует, что для этого сечения f( ) + ( ) = 0 или

	l		l
t		f t		,	(7.43)

	c		c

т. е. обратная волна является отражением прямой с переменой знака.

При мгновенном закрытии задвижки (при υ = 0) из (7.42) имеем f = –cυ0, следовательно, = cυ0. При своем движении вправо волна , складыва-

ясь с f, дает p – p0 = 0. Волна достигнет нулевого сечения за время Т=2l/с, здесь она отражается от заслонки без изменения знака и начинается распространение влево волны разрежения.

Если время закрытия задвижки tз < T, то максимальное давление определится уравнением (7.31), а удар называется прямым гидравлическим ударом. Если tз > T, то возникающий при этом гидравлический удар называется непрямым. Максимальный перепад давлений, возникающий при таком ударе, можно найти на основе анализа, аналогичного приведенному выше, и рассчитать по

приближенной формуле				k			,
	p p0		k
	p p0		k		k 2	4
					k 2	4
	p	2
0

где

k cυ0 T 2 p0 tз

Выполненный анализ показывает, что давление прямого гидравлического удара не зависит от длины трубопровода и значительно по величине. Так, при течении воды (ρ = 10 3 кг/м3; с = 1435 м/с) со скоростью υ0 = 1 м/с р = р – р0 = 1,435106 Па 14 ат.

Возможны следующие способы уменьшения ударного давления:

1установка запорной арматуры, не допускающей быстрого закрытия трубопровода.

vk.com/club152685050 | vk.com/id446425943

2уменьшение инерционных сил путем установки воздушного колпака (рис. 7.24). Здесь время остановки жидкости увеличено за счет сжимаемости газа.

Рисунок 7.24 – Схема трубопровода с

воздушным колпаком

7.10 Высота всасывания центробежного насоса

По мере увеличения высоты h (рис. 7.25) установки насоса давление в жидкости перед насосом уменьшается.

Предельное минимальное давление в жидкости равно давлению насыщенных паров рн.п. При р = рн.п происходит парообразование в жидкости, т. е. начало ее кипения. Образовавшаяся парожидкостная смесь при последующем перемещении в межлопаточном пространстве колеса насоса попадет в область повышенных давлений (р > рн.п). Здесь происходит быстрая конденсация паров, жидкость мгновенно заполняет остающиеся полости, происходят гидравлические удары, вызывающие появление микротрещин на поверхности деталей насоса, а затем и разрушение их. Описанное явление называется кавитацией.

			1	D1/2
			1
		а
		а		1
hmax		l, d
		l, d
		z
0	p0	0
0		0	x
			x

Рисунок 7.25 – Высота всасывания центробежного насоса

100

hдоп= f(Q)

vk.com/club152685050 | vk.com/id446425943

повышенных давлений (р > рн.п). Здесь происходит быстрая конденсация паров, жидкость мгновенно заполняет остающиеся полости, происходят гидравлические удары и, если полости находились на стенке, то гидравлические удары вызывают появление микротрещин на поверхности деталей насоса, а затем и разрушение их. Описанное явление называется кавитацией. Недопустимо эксплуатировать насос при наличии кавитации, т. е. необходимо соблюдать условие, чтобы давление в насосе р > рн.п. В соответствии с уравнением Бернулли (7.7) давление в жидкости понижается с увеличением высоты и с ростом скорости течения жидкости. Наибольшая скорость на участке всасывания имеет место при входе жидкости на лопатки колеса u1, при этом логично рассматривать самую верхнюю точку 1 (z1 = h + D1/2). Составим уравнение Бернулли для сечений 0 к 1 (см. рис. 7.25). В сечении 0: z0 = 0; р0; υ0 = 0; в сечении 1: z1 = h + D1; p = р1; υ1 = u1. Гидравлические потери на участке 0 – 1 можно представить в виде

hw hвс hнас

где hвс – гидравлические потери во всасывающей линии, т. е. на участке 0 – а; hнас – потери внутри насоса в зоне всасывания, т.е. на участке а – 1, опре-

деляемые формулой

нас 2g

нас

Решив уравнение (7.7) относительно hmax, найдем

p0 p1

hmax

hвс

нас

Обозначим

u12

доп

нас

Коэффициент нас, скорость u1 зависят только от конструктивных размеров и производительности насоса.

Величина hдоп называется «кавитационным запасом». Зависимость

для каждого насоса определяется экспериментально и приводится в паспорте центробежного насоса в качестве одной из основных его характеристик.

7.11 Высота всасывания поршневого насоса

Если поршень насоса имеет кривошипно-шатунный привод (cм. рис. 7.26), то движение жидкости в системе является неустановившемся.

101

vk.com/club152685050 | vk.com/id446425943

	х
	1	L
		L	R
			R
D/2	1
D/2

		lв, Sв
h		lв, Sв
h


			z
	υв		z
0		0

Рисунок 7.26 – Высота установки поршневого насоса

Если длина шатуна L существенно больше радиуса кривошипа R, то приближенно его скорость с будет равна

c	dх	d	(R R cos ) R sin .	(7.44)
	dt	dt

Ускорение поршня

ac 2 R cos .

пt

Согласно (2.17) скорость несжимаемой жидкости во всасывающем трубопроводе

υв cS Sв ,

(7.45)

где S – площадь поршня; Sв – площадь сечения всасывающего трубопровода. Соответственно ускорение жидкости во всасывающем трубопроводе


a	υ	c S		а	S		.	(7.46)

	t	t S
в			в	п S		в

Для расчета допустимой высоты установки насоса следует воспользоваться уравнением Бернулли (7.6) при неустановившемся течении жидкости.

Применим его для сечений 0 и 1 (см. рис. 7.26). В сечении 0 – 0: z0 = 0; р = p0, υ0 = 0. В сечении 1 – 1: z1 = h + D/2; p = p1; υ1 = c.

102

vk.com/club152685050 | vk.com/id446425943

		lв		2		с	2
hw	в		в	υв	кл			,	(7.47)
		dв		2g		2g

где первое слагаемое включает потери во всасывающем трубопроводе, а второе

– потери внутри насоса (главным образом гидравлические потери во всасывающем клапане).

Удельную энергию необходимую для преодоления инерции потока можно рассчитать по формуле

u dl aв dl aп dx

aп dl aп dx .

l t

Sв l

С учетом (7.44) и (7.45) получим

u dl ап

x lв

(7.48)

Sв

С учетом (7.44) – (7.47) уравнение Бернулли можно представить в виде

p0 pн.п

Asin2 B cos C cos2 ,

(7.49)

max

где

lв

A 1 кл

;

dв

Sв

R ;

B R lв

Sв

С R 2 .

Уравнение (7.48) показывает, что hmax = f( ). Физически очевидно, что в качестве расчетной можно принять лишь минимальное из значений hmax.

Найдем положение кривошипа, т. е. угол , отвечающее минимуму функции (7.48). Для этого вычислим и приравняем нулю производную

dhmax	2Acos B 2C cos sin 0 ,	(7.50)

d

Условие (7.49) выполняется (и возможен минимум) при 1 = 0 или при

		В
2	arccos		.

		2 А С

103

vk.com/club152685050 | vk.com/id446425943

Из двух найденных значений угла φ в качестве расчетного следует признать то, при котором hmax минимально.

Для увеличения допустимой высоты всасывания нередко перед насосом на линии всасывания устанавливают воздушный колпак (рис. 7.27). При этом на участке всасывающего трубопровода имеет место, практически установившееся течение жидкости.

		х
		1
	D/2	1
	D/2	c
		c

	υв1, lв1, Sв1
h	lв, Sв
υв	z
0	0
	х

Рисунок 7.27 – Схема установки поршневого насоса

с воздушным колпаком

Неустановившимся течение остается лишь на коротком трубопроводе между колпаком и насосом и внутри самого насоса. В этом случае следует принять υв = Q/Sв, где Q = 2RSn = const – производительность насоса. С учетом (7.45) и (7.46) для υв1 и ав1 соответственно, из (7.6) получим уравнение аналогичное (7.49)

pн.п

h Asin2 B cos C cos2 ,

max

где

lв

hв

υв

;

dв

lв1

кл

вx

в1

;

dв1 Sв1

104

vk.com/club152685050 \| vk.com/id446425943
				2
				R .
	B R lв1		S	R .
			Sв1	g
Характерные для этих случаев зависимости hmax = f( ) представлены на
рисунке 7.28.
hmax,
м
13			1
			1
11
9
	2
7
5
3 0	0,2	0,4	0,6	0,8	, рад
1 – hmax = f( ) без колпака; 2 – hmax = f( ) с колпаком

Рисунок 7.28 – Зависимость высоты установки поршневого насоса от угла поворота кривошипа

Из анализа рисунка 7.28 следует, что воздушный колпак существенно увеличивает допустимую высоту установки поршневого насоса.

7.12 Трубопровод с путевым расходом

Рассмотрим тупиковый трубопровод с цилиндрическими насадками, расположенными с постоянным шагом l (рисунок 7.29).

Выясним, при каких условиях расход через каждое из отверстий Qi будет примерно одинаков. Согласно (7.20), для нахождения Qi необходимо знать давление над отверстием. Установим характер распределения давлений вдоль оси трубы. Для этого составим уравнение Бернулли для каждого участка оросителя: для сечений i и i + 1 (рисунок 7.29)

p	α		υ2	p	α		υ2	h
i			i	i 1			i 1		.	(7.51)
						i 1 2g			.	(7.51)
ρg		i 2g ρg				i 1 2g		w, i 1

Суммарные потери на участке трубы состоят из потерь по длине hl и потерь при внезапном расширении hв.р потока, вызванном локальным оттоком части жидкости (см. рис. 7.29). С учетом (7.10) и (7.18) получим

105

vk.com/club152685050 | vk.com/id446425943

	λ		l	υ2	υi	υi 1	2
h				i 1			,	(7.52)
h		i 1 D 2g					,	(7.52)
w, i 1		i 1 D 2g				2g

			i
Q0	υ1		υi			υi+1		υn	D
									D
			i						d
			0Qi	0					d
	Q1		0Qi	0	Qi+1		Qn
				pатм
	Рисунок 7.29 – Трубчатый ороситель
Из (7.51) и (7.52) следует
	p	p υ		υ υ		D υi2 1 .			(7.53)
	i 1	i	i 1	i i 1		i 1 l	2

Анализ уравнения (7.51) показывает, что при hw = 0 давление вдоль оси трубы должно возрастать (линия 1 на рис. 7.30 и 7.31). При возрастании гидравлических потерь по длине hl. возможно и уменьшение давления (линии 3 – 6 на рис. 7.30 и 7.31). Составив уравнения вида (7.51) и (7.52) для всех участков трубы и учитывая, что

n
Q0 Qi ,	(7.54)

i 1

где Q0 – полный расход жидкости в трубе, а Qi определяется по уравнению (7.20), получим замкнутую систему уравнений.

Для расчета коэффициентов сжатия и коэффициента расхода при исте-

чении жидкости через цилиндрические насадки воспользуемся соотношениями

0,5

0,05

0,6 1 exp 0,75x

;

1 , (7.55)

i 1

где

gHi 1

0,8

; H

pi 1

(7.56)

i 1

υ2

i 1

106

vk.com/club152685050 | vk.com/id446425943

Результаты численного решения системы уравнений (7.51) – (7.52), (7.54) с учетом (7.55) – (7.56) при условии, что на всех участках гидравлически гладкой трубы режим течения турбулентный, приведены на рисунках 7.30 – 7.32.

2p
ρυ02
3,5
	6
3									1
	5								1
	5
2,5	4								2
2,5	3								2
	3
	2								3
2	2
2	1								4
									4
									5
									5
1,5									6
1 0	1	2	3	4	5	6	7	8	9
1 – 0; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; 6 – 1

Рисунок 7.30 – Распределение давления по длине
оросителя при различных отношениях l/D
2(pi – p0)
ρυ02						1
						1
0,5
						2
0
–0,5						3
–0,5
–1						4
–1
–1,5						5
–1,5
–2						6
–2
–2,50	1	2	3	4	5	6	7	8	9
1 – 0; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; 6 – 1

Рисунок 7.31 – Распределение разности давлений по длине оросителя при различных отношениях l/D

Характер распределения относительных величин давления р/(ρυ02/2) (рис. 7.30) и разности давлений (рi – p0)/(ρυ02/2) (рис. 7.31) по длине трубопровода так же, как и распределение расходов жидкости через патрубки Qi (рис.7.32), существенно зависят от параметра l/D.

107

vk.com/club152685050 | vk.com/id446425943

Если задача проектировщика оросителя состоит в обеспечении наиболее равномерного стока жидкости по длине оросителя, то оптимальным следует признать ороситель, описываемый линией 6 на рисунке 7.32.

Q 103,
м3/с
									1
0,08									2
0,08									3
									3
									4
									5
0,06									6
0,06			6
			6
		5
0,04			4
0,04			3
			3
			2
0,02			1
0,02	1	2	3	4	5	6	7	8	9
1 – 0; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; 6 – 1

Рисунок 7.31 – Распределение расходов жидкости через отверстия по длине оросителя при различных отношениях l/D

Отметим, что равномерное распределение давления не означает равномерный сток жидкости по длине оросителя.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Физический смысл уравнения Бернулли и его слагаемых.

2 Каков физический смысл коэффициента Кориолиса?

3 В каком случае нарушается гидростатический закон распределения давлений в живом сечении?

4 Что следует понимать под местным сопротивлением и как рассчитать hм.с? 5 Как рассчитать потери по длине?

6 Может ли быть инерционный напор < , = , > 0?

7 Какие параметры жидкости, трубопровода влияют на потери напора? 8 Что представляют собой коэффициенты истечения?

9 Как взаимосвязаны коэффициенты сжатия, скорости, расхода, и местного сопротивления малого отверстия? Каков физический смысл этих коэффициентов?

10 Что такое полное и неполное, совершенное и несовершенное сжатие струи? 11 Почему при установке насадка увеличивается расход по сравнению с исте-

чением через отверстие одинакового сечения?

12 В чем принцип действия расходомера с соплом Вентури?

13 В чем разница между линейными потерями и квадратичными?

14 От каких факторов в общем случае зависят значения коэффициентов местных сопротивлений?

108

vk.com/club152685050 | vk.com/id446425943

15 В каком случае потери напора будут больше – при внезапном расширении или при внезапном сужении труб (соотношение диаметров в обоих случаях одно и то же, другие параметры потока одинаковы)?

16 При выполнении какого условия отверстие называется малым?

17 Сравните гидравлические характеристики отверстий и насадков.

18 Какие допущения приняты при рассмотрении истечения жидкости при переменном напоре?

19 Какое давление возникает внутри цилиндрического насадка при истечении в атмосферу? Каково условие нормальной работы насадка?

20 От чего зависит время опорожнения резервуара?

21 Что называется водосливом?

22 Каковы основные причины возникновения вторичных течений в движущейся жидкости?

23 Поясните принцип действия трубки Пито-Прандтля.

24 Каков принцип действия ротаметра?

25 В каких измерительных приборах используются закономерности уравнения Бернулли?

26В чем разница между трубкой Пито и трубкой Пито-Прандтля?

27Чему равна скорость распространения волны гидравлического удара в случае недеформируемых стенок трубопровода (Е = )?

28Как надо закрывать задвижку в трубопроводе, чтобы уменьшить давление, возникающее при гидравлическом ударе, – быстро или медленно?

29Как будет изменяться ударное давление при увеличении диаметра трубы и сохранении толщины ее стенки?

8 СЖИМАЕМЫЕ ЖИДКОСТИ

8.1 Одномерное движение идеального газа

Вгидромеханике обычно не различают понятия «газ» и «жидкость», т. к. газы ведут себя как ньютоновские жидкости. Однако в технических устройствах при течении газов часто необходимо создать скорости, превышающие 0,1 скорости звука, и математическое описание их поведения следует проводить с учетом сжимаемости.

Вшироком диапазоне изменения температур Т и давлений p для газов применимо уравнение состояния в виде (1.3).

При высоких скоростях течения газов изменение давления в канале приводит к изменению его температуры, поскольку за короткое время не успевает произойти теплообмен с внешней средой, а изменение состояния газа происходит практически адиабатически.

Первое начало термодинамики позволяет сделать вывод, что при адиабатическом процессе давление и плотность связаны соотношением

p	p0	const ,	(8.1)
k	k	const ,	(8.1)
k	k
	0

109

vk.com/club152685050 | vk.com/id446425943

где k = cp/cV – показатель адиабаты, cp – удельная теплоемкость при постоянном давлении, сV – удельная теплоемкость при постоянном объеме.

Выражение (8.1) для вычисления скорости звука с учетом равенства (1.3) принимает вид

a k	p	.	(8.2)

При течении идеального газа скорость во всех точках живого сечения канала постоянна, т. е. средняя расходная скорость υ равна локальной скорости u. С учетом этого уравнение неразрывности, т. е. условие постоянства массовых расходов в двух живых сечениях канала, при условии переменности плотности газа по длине канала, имеет вид

1u1S1 2u2 S2 const ,

(8.3)

где u1 и u2 — средние расходные скорости в сечениях 1 и 2, площади которых равны соответственно S1 и S2.

Поскольку плотность газов, как правило, невелика, то массовыми силами по сравнению с силами давления в уравнениях движения идеальной жидкости (уравнение (5.2)) можно пренебречь, т. е. принять Fx = Fy = Fz = 0.

Уравнение Бернулли (5.7), получаемое в результате интегрирования (5.2) вдоль линии тока, дифференциальное уравнение которой (2.1), в этом случае упрощается до вида

	1			2
		dp d	u		0 .	(8.4)

		2
Интегрирование уравнения (8.4) при условии адиабатического поведения
газа (8.1) позволяет найти интегральную форму уравнения Бернулли:

		u2					k			p	u2								k		p
	1									1				2									2	const .	.	(8.5)
							1													1				const .	.	(8.5)
2						k	1					2						k		1			2
									1														2
С учетом выражения (8.2) уравнение (8.5) можно записать в виде
					u2					a2					u2					a2
					1				1							2				2			const ,			(8.6)
			2						k 1							2				k 1			const ,			(8.6)
			2						k 1							2				k 1
или с учетом (1.3)
		u2					k			RT			u			2				k		RT const ,
		1														2										(8.7)
																										(8.7)
2						k 1			1					2					k 1					2
2						k 1								2					k 1
а с учетом соотношения ср = Rk/(k – 1)
					u2								u2
				1				c T								2	c T					const .				(8.8)
								c T									c T					const .				(8.8)
			2							p 1				2						p 2
			2											2
																110

vk.com/club152685050 | vk.com/id446425943

Уравнение неразрывности (8.3) после взятия производной по длине канала (ось x) с учетом выражений (8.4) и (8.2) можно представить в виде [3]

		2			u	dS
	u		1	du			.	(8.9)
		2
a			dx		S dx

Уравнение (8.9) позволяет провести качественный анализ характера движения сжимаемого газа в канале переменного сечения, результаты которого представлены в таблице 8.1.

Таблица 8.1 – Характеристика движения сжимаемого газа в канале переменного сечения

Изменение сечения по	Соотношение	Изменение скорости по
длине канала	cкоростей	длине канала, dux/dx
Сечение уменьшается	u < a	dux/dx > 0
(конфузор), dS/dx < 0	u > a	dux/dx < 0
Сечение увеличивается	u < a	dux/dx < 0
(диффузор), dS/dx > 0	u > a	dux/dx > 0

Из формулы (8.9) или таблицы 8.1 следует, что для получения дозвуковых скоростей истечения (u < a) необходимо иметь сужающийся канал (конфузор); для достижения сверхзвуковых скоростей необходимо сначала иметь конфузор (где газ разгоняется до скорости звука) и расширяющийся канал (диффузор), который позволит достичь сверхзвуковых скоростей. Канал с такой геометрией называется в технике соплом Лаваля.

Истечение газа из бака через сужающееся сопло (рисунок 8.1).

Уравнение Бернулли (8.7), составленное для сечений 0–1 как

	k	p	u2	k p
		0			,	(8.10)
	k 1 0		2	k 1

с учетом равенства (8.2) можно представить в виде

k 1

(8.11)

1 0

111

vk.com/club152685050 | vk.com/id446425943

p0 u

u0 = 0

Рисунок 8.1 – Истечение газа из бака через сужающееся сопло

С ростом давления p0 скорость истечения растет, но она может достичь лишь значения местной скорости звука, определяемой совместным решением уравнений (8.10) и (8.2) зависимостью

RT .

(8.12)

max

k 1

Дальнейший рост давления не приводит к росту скорости истечения. Минимальное давление p0кр, при котором скорость истечения газа равна

скорости звука, называется критическим давлением. Оно определяется соотношением

								k
	p0кр			2
	p0кр			2				k 1
							.		(8.13)
							.		(8.13)
	p	k 1
Плотность газа на выходе его из сопла можно вычислить по соотношению
(8.1):
				1

0			p			k
			p		.				(8.14)
					.				(8.14)
			p0

Истечение газа из бака через сопло Лаваля (рисунок 8.2).

Для получения сверхзвуковых скоростей необходимо, как следует из анализа уравнения (8.9), сначала в сужающемся канале разогнать газ до скорости звука. Тогда при последующем течении в диффузоре (см. табл. 8.1) произойдет дальнейшее увеличение скорости.

При известных параметрах газа в баке p0, T0 плотность газа 0 может быть рассчитана по формуле (8.1), а скорость истечения – по формуле (8.11).

112

vk.com/club152685050 | vk.com/id446425943

		p


			uc
	p0
				u
				u


u0 = 0
u0 = 0			pc
			pc

Рисунок 8.2 – Истечение газа из бака через сопло Лаваля

Плотность вытекающего газа в сечении 1 найдем по уравнению (8.14). Зная плотность и давление p, по формуле (8.2) найдем локальную скорость звука a. Если при заданном давлении p0 выполняется условие u > a, то следует в проектируемом сопле создать минимальное сечение, т. е. применять сопло Лаваля. Скорость в сжатом сечении должна быть равна местной скорости звука, которую можно найти по формуле (8.12).

Решив совместно соотношение (8.1), записанное для сечений 1 и С, и уравнение (8.2), составленное для параметров газа в сечении С, найдем

			1
		2
				k 1
C	0		.		(8.15)

	k 1

Соотношение площадей сечений С и 1 найдем из уравнения неразрывно-

сти (8.3):

SC	C uC	.	(8.16)

S	u

КОНТРОЛЬНЫЕ ВОПРОСЫ 1 Какое свойство газа характеризует скорость звука?

2Основная идея сопла Лаваля.

3Какой процесс называется адиабатным?

4Что такое показатель адиабаты?

113

vk.com/club152685050 | vk.com/id446425943

Литература

1Шлихтинг, Г. Теория пограничного слоя / Г. Шлихтинг. – М.: Наука,

1974. – 712 с.

2Лойцянский, Л.Г. Механика жидкости и газа / Л.Г. Лойцянский. – 6-е

изд. – М.: Наука, 1987. – 848 с.

3Слезкин, Н.А. Динамика вязкой несжимаемой жидкости / Н.А. Слезкин. – М.: Гос. изд. техн-теор. лит., 1955. – 520 с.

4Седов, Л.И. Механика сплошных сред. Ч. 1./ Л.И. Седов – М.: Наука,

1976. – 528 с.

5Кочин, Н. Е. и др. Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. Часть II / Н. Е. Кочин, И. А. Кибель, Н. В. Розе – М.: Физматгиз, 1963. – 728 с.

6Повх, И.Л. Техническая гидромеханика / И.Л. Повх. – Л.: Машино-

строение, 1976. – 504 с.

114

vk.com/club152685050 | vk.com/id446425943

Приложение А

(рекомендуемое)

Векторы и операции над ними

Полем какой-либо величины называется пространство, в каждой точке которого эта величина вполне определена. Если эта величина скаляр, т. е. характеризуется одним числом, то поле называют скалярным (поле плотности, поле температуры).

Векторным называется поле, которое характеризуется в каждой точке пространства величиной и направлением. Поэтому непременным условием, связанным с векторными величинами, является то, что они должны складываться по правилу параллелограмма.

Единичные векторы (орты) в декартовой системе координат будем обо-

значать i , j, k . Тогда вектор u может быть представлен как
u i ux j uy k uz	(А.1)

где ux , uy , uz – проекции (компоненты) вектора на соответствующие оси координат.

Скалярное произведение двух векторов дает скалярную величину

u υ	u	υ	cos ,	(А.2)
u υ	u	υ	cos ,	(А.2)

где – угол между векторами.

Ясно, что скалярное произведение обращается в нуль, если векторы u и

υвзаимно перпендикулярны.

Векторным произведением двух векторов в противоположность ска-

лярному, является вектор. Векторное произведение может быть записано в виде определителя третьего порядка

	i	j	k
u υ	ux	uy	uz	(А.3)
	υx	υy	υz

Раскрывая определитель по общим правилам, получим:

u υ i uyυz uzυy j uxυz uzυx k uxυy uyυx

(А.4)

Операции первого порядка

(дифференциальные характеристики поля)

В теории поля рассматриваются три так называемые операции первого порядка. Эти операции позволяют, выполнив определенные математические действия превратить

115

vk.com/club152685050 | vk.com/id446425943

-скалярную величину в векторную;

-векторную величину в скалярную;

-векторную – в другую векторную;

Эти операции соответственно называются: градиент, дивергенция и ротор (вихрь). Рассмотрим каждую из них.

Градиент какой-то скалярной функции (x, y, z) есть вектор, образующийся в результате выполнения следующих действий:

grad i			j	k .			(А.5)
		x		y		z
Физически градиент есть вектор, в направлении которого функция в дан-
ной точке поля изменяется с максимальной скоростью.
Дивергенцией вектора u называется выражение вида
div u	u	x	uy		u	z	(А.6)

			y		z
	x

Следовательно, любое векторное поле дает некоторое скалярное поле, а именно поле своей дивергенции (расходимости). Если div u 0 , то поле называют соленоидальным.

Вихрь поля (ротор) – это вектор, образующийся при выполнении опера-

ции

rot u i uz

uy	ux
	j
z		z

u		uy		u	x
	z	k				(А.7)

x			x	y

Если rot u 0 , то поле называют безвихревым.

Для обозначения этих операций широко исп ользуется оператор

Набла – .

Каждая из трех операций имеет гидродинамическую интерпретацию, которая приводится в соответствующих разделах курса.

Операции второго порядка

Операции grad , div u, rot u , переводящие скаляр в вектор, вектор в скаляр и вектор в вектор порождают пять операций второго порядка:

- превращение скалярной величины в векторную

grad div u ;

- превращение векторной величины в скалярную

div grad ; div rot u ;

- превращение одной векторной величины в другую

rot grad ; rot rot u .

116

vk.com/club152685050 | vk.com/id446425943

В теории поля показывается, что
div rot u 0; rot grad 0.
Операция div grad носит название оператора Лапласа для скалярного
поля и имеет вид
2 div grad	2	2	2	(А.8)
2 div grad	x2	y2	z2	(А.8)
	x2	y2	z2

Интегральные соотношения теории поля

Поток векторного поля

Пусть dS (рис. А.1) – элемент поверхности, а n – единичный вектор, направленный по внешней нормали. Потоком векторного поля (например, u ) называют поверхностный интеграл вида

u ndS undS udSn .			(А.9)
S	S	S

Рисунок А.1 – К определению понятия потока векторного поля.

Если рассматривается векторное поле ротора ( rоt u ), то поток этого поля представляется как

rоt u ndS .	(А.11)
S
Циркуляция вектора поля
Пусть рассматривается векторное поле какой-то величины u . Циркуляци-
ей вектора u вдоль контура L называют криволинейный интеграл вида
u d l	(А.12)
L

Иногда этот интеграл интерпретируется как «работа» векторного поля вдоль контура L. Если циркуляция векторного поля вдоль замкнутого пути (контура) равна нулю, то поле называют потенциальным.

117

vk.com/club152685050 | vk.com/id446425943

Формула Стокса

Эта формула позволяет преобразовать криволинейный интеграл вдоль замкнутой пространственной кривой в поверхностный интеграл по поверхности, натянутой на эту кривую, т. е.

u dl	rotu ndS ,	(А.13)
L	S

т. е. циркуляция вектора поля вдоль контура равна потоку вихря через поверхность, ограниченную этим контуром.

Формула Остроградского – Гаусса

Это соотношение, часто называемое преобразованием Остроградского – Гаусса, связывает поверхностный интеграл по замкнутой поверхности с интегралом по объему, ограниченному этой поверхностью

u ndS div udV .		(А.15)
S	V

Формула показывает, что поток векторного поля через замкнутую поверхность равен интегралу от дивергенции поля по объему, ограниченному этой поверхностью.

В механике жидкости широко используется формула, являющаяся следствием формулы Остроградского – Гаусса для скалярного поля

ndS grad dV ,		(А.16)
S	V

где – какая-то скалярная функция.

Приложение В

(рекомендуемое)

Компоненты векторов и основные уравнения в криволинейных координатах

Связь криволинейных координат с прямоугольными

Цилиндрические координаты r, , z


r		x2 y2 ;	x rcos ;
arctg y x ;			y rsin ;	(В.1)
z z;			z z.
Элемент дуги пространственной кривой выражается через приращения
цилиндрических координат dr, d , dz посредством соотношения
ds2 dx2	dy2 dz2		dr2 r2d 2 dz2 .	(В.2)
	118

vk.com/club152685050 | vk.com/id446425943

Сферические координаты r, ,


r	x2 y2 z2 ;				x r sin cos ;

		x2	y2
arctg				;	y r sin sin ;
arctg				;	y r sin sin ;
			z

arctg y			x ;		z r cos .

Для элемента дуги справедливо соотношение

ds2 dx2 dy2 dz2 dr2 r2d 2 r2sin2 d 2 .

Взаимосвязь между проекциями вектора

υr	υx cos υysin ;	υx	υr cos υ sin ;
υ	υxsin υy cos ;	υy	υr sin υ cos ;
	υz υz ;		υz υz .

υr υxsin cos υysin sin υz cos ; υx cos cos υy cos sin υxsin ;

υ υxsin υy cos ;

υx υr sin cos υ cos cos υ sin ; υy υr sin sin υ cos sin υ cos ; υz υr cos υ sin .

Формулы связи матриц р1Т и Т в цилиндрической (r, , z) и

сферической системах координат

Цилиндрические координаты r, , z

	r	p 2 ur ;
	r			r
				r
		u	r		1	u
p 2			r				;
p 2					r		;
		r			r
	r	p 2 uz ;
	r			z
				z

1 u

;

1 u

;

119

(В.3)

(В.4)

(В.5)

(В.6)

(В.7)

vk.com/club152685050 | vk.com/id446425943

Сферические координаты r, ,

p 2 ur ;

ctg

p 2

;

r rsin

p 2

;

1 u

;

(В.8)

rsin

	1	u	1	u	u ctg
						.
						.
rsin			r		r

Уравнение неразрывности

Цилиндрические координаты r, , z

Сферические координаты r, ,

1 u

u ctg

r sin

Уравнение Навье-Стокса

Цилиндрические координаты r, , z

r u

z z

1 p

;

ur u

r r

1 p

2 ur

;

p u

где оператор Лапласа имеет вид

r r r2

(В.9)

(В.10)

(В.11)

120

vk.com/club152685050 | vk.com/id446425943

Сферические координаты r, ,

u2 u2

rsin

1 p

ctg

;

u u

u2ctg

rsin

1 p

2cos

2 u

;

sin

ctg

r sin

2cos

2 ur

r sin

sin

(В.12)

где оператор Лапласа имеет вид
	2	2	1		2	ctg	1	2	.

	r2	r r	r	2	2	r2	r2sin2 2
	r2	r r	r	2	2	r2	r2sin2 2

121

vk.com/club152685050 | vk.com/id446425943

Кафедра оптимизации химической и биотехнологической аппаратуры

ОСНОВЫ ГИДРОМЕХАНИКИ

Учебное пособие

Доманский Игорь Васильевич Некрасов Виктор Алексеевич

__________________________________________________________________

Отпечатано с оригинал-макета. Формат 60×90 1/16 Печ. л. 7,6. Тираж 100 экз. Заказ № от 2015

__________________________________________________________________

Санкт-Петербургский государственный технологический институт (технический университет)

__________________________________________________________________

190013, Санкт-Петербург, Московский пр., 26 Типография издательства СПбГТИ (ТУ) тел. 49-49-365

122

vk.com/club152685050МИНИСТЕРСТВО| vk.com/id446425943ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ НЕФТИ И ГАЗА ИМЕНИ М.С. ГУЦЕРИЕВА

Программа профессиональной переподготовки «Разработка месторождений нефти и газа»

Практическое задание

По дисциплине: Гидромеханика.

Выполнил:

Суфиянов Кирилл Анатольевич

группа 01-ПП/2018

Научный руководитель:

Ганзий Юлия Валентиновна

Ижевск 2018

vk.com/club152685050 | vk.com/id446425943

vk.com/club152685050 | vk.com/id446425943

Экзаменационные вопросы по дисциплине «Гидромеханика»

1.Основные свойства жидкостей

2.Основные модели жидкостей

3.Классификация сил в жидкости

4.Условия отсутствия в жидкости касательных напряжений

5.Свойства давлений в отсутствие касательных напряжений

6.Дифференциальные уравнения равновесия жидкостей

7.Основной закон гидростатики

8.Закон Паскаля

9.Закон Архимеда

10.Методы изучения движения жидкости

11.Линия тока и её уравнение. Трубка тока и жидкая струйка

12.Уравнение неразрывности в общем виде

13.Уравнение неразрывности для трубки тока

14.Плоские течения. Основные свойства (перечислить)

15.Функции тока. Основные свойства.

16.Вихревые движения. Основные свойства

17.Теорема Стокса

18.Обтекание тела вязкой жидкостью. Понятие о пограничном слое

19.Безвихревые движения. Основные свойства (перечислить)

20.Метод сложения потенциальных потоков

21.Плоский диполь

22.Дифференциальные уравнения движения в форме Эйлера

23.Уравнение Бернулли

24.Интеграл Эйлера

25.Истечение жидкости из открытого бака

26.Распределение давления поперек плавно изменяющегося потока

27.Бесциркулярное обтекание цилиндра. Парадокс Даламбера

28.Обтекание цилиндра циркуляционным потоком

29.Применение закона количества движения для определения гидродинамической силы на равномерно движущемся теле

30.Сопротивление ускоренно движущегося осесимметричного тела. Понятие о присоединенной массе

31.Общий случай неравномерного движения тела. Обобщенные присоединенные массы

32.Присоединенные массы. Общий случай

33.Основная аксиома теории размерностей

34.Критерии динамического подобия: физический смысл, назначение

35.Моделирование динамических процессов

36.Дифференциальные уравнения движения вязкой жидкости. Граничные условия

37.Режимы течения вязкой жидкости их характеристики

38.Уравнение Бернулли для струи идеальной жидкости

39.Уравнение Бернулли для струи вязкой жидкости

40.Потери напора и коэффициенты сопротивления

41.Ламинарное течение в круглой трубе

42.Турбулентное течение в трубе

vk.com/club15268505043. Влияние шероховатости| vk.com/id446425943на сопротивление труб. Гидродинамически гладкие поверхности

44.Обтекание теля вязкой жидкостью. Понятие о пограничном слое

45.Явление отрыва пограничного слоя

46.Сопротивление хорошо обтекаемых тел

47.Сопротивление плохо обтекаемых тел

48.Основные свойства волн

49.Плоские волны малой крутизны: отличительные признаки, скорость распространения

50.Затухание вол с глубиной

51.Потенциальная энергия волн

52.Кинетическая энергия волн

53.Энергия волн. Общие сведения

54.Геометрические характеристики крыла

55.Гидродинамические характеристики крыла

56.Механизм возникновения подъемной силы на крыле

57.Влияние вязкости на гидродинамические характеристики крыла

58.Особенности обтекания крыла конечного размаха. Понятие об индуктивном сопротивлении

59.Понятие о кавитации. Виды кавитации

60.Условия возникновения кавитации на теле

61.Влияние кавитации на гидродинамические характеристики крыла

vk.com/club152685050 | vk.com/id446425943

3.КИНЕМАТИКА ЖИДКОСТИ

3.1.Основные сведения из теории, расчетные формулы

иметодические указания

Вданном разделе рассматривается в основном плоское течение, т.е. одинаковое во всех плоскостях, перпендикулярных некоторой оси (поперечное обтекание цилиндрических тел и т.д.). Выбрав эту ось за одну из осей координат (например, за ось z), получаем, что для всего поля течения соответствующая проекция скорости равна нулю ( vz =0).

Движение жидкости можно изучать с помощью метода Эйлера, в котором рассматривается изменение совокупности характеристик течения и свойств жидкости в функции от координат точек пространства и времени. Например,

поле скорости может быть задано в виде скалярных функций:
vx = vx (x, y,t ) ;	vy = vy (x, y,t ) .	(3.1)

По теореме Коши-Гельмгольца движение жидкой частицы можно представить состоящим из трех составляющих: поступательного движения вместе с полюсом, вращения вокруг полюса и деформационного движения. Характеристикой вращательного движения служит угловая скорость

∂vy

∂v

ω =

rot v

или

−

(3.2)

∂x

∂y

Деформационное движение характеризуется относительными скоростями линейной деформации:

εx = ∂vx ∂x ; εy = ∂v y ∂y

и относительной скоростью деформации сдвига (угловой деформации)

∂vy

∂v

∂x

∂y

Ускорение частицы в эйлеровых переменных:

∂v

+ vx

∂v

+ vy

∂v

;

∂t

∂x

∂y

(3.3)

(3.4)

(3.5)

dvx

∂vx

+ vx

∂vx

+ vy

∂vx

;

dvy

∂vy

+ vx

∂vy

+ vy

∂vy

∂t

∂x

∂y

∂t

∂x

∂y

Первое слагаемое ∂

∂t представляет собой локальное, или местное, ус-

корение, вызываемое нестационарностью поля скорости. Остальные слагаемые - конвективное или переносное ускорение, вызываемое неоднородностью поля скорости. По формулам (3.2) – (3.5) при известном поле скорости (3.1) можно определить все характеристики движения жидкой частицы, а также найти семейства линий тока и траекторий.

Линией тока называется линия, в каждой точке которой вектор скорости в рассматриваемый момент направлен по касательной. Дифференциальное уравнение семейства линий тока имеет вид

vk.com/club152685050 | vk.com/id446425943

dx	=	dy	.	(3.6)
vx
		vy

Траекторией частицы называется след ее движения в пространстве (в случае плоских течений в плоскости). В случае установившегося течения, характеристики которого во всех точках пространства не зависят от времени, локальная составляющая ускорения равна нулю ∂v∂t =0, а линии тока и траекто-

рии совпадают.

Течение жидкости (без разрывов) удовлетворяет уравнению неразрывности, выражающему закон сохранения массы. Это уравнение в дифференциальной форме для несжимаемой жидкости имеет вид

∂vx

∂v y

= 0

(3.7)

∂x

∂y

или в важной для практических приложений полярной системе координат

∂vr

1 ∂vθ

= 0 ,

(3.8)

∂r

r ∂θ

для элементарной трубки тока

vdS = dQ = const,

(3.9)

где dQ - объемный расход через сечение;

dS - площадь сечения, нормального

линиям тока (в случае плоских течений площадь сечения dS = dl 1, dl - эле-

мент в плоскости Оху, 1- высота сечения вдоль Оz).

Кинематический анализ потока жидкости с заданным полем скорости (3.1) включает: 1) проверку удовлетворения уравнению неразрывности (3.7) или

(3.8);

2) определение характеристик движения жидкой частицы

( ωz , εx , εy , θz , dv / dt ) по формулам (3.2) – (3.5);

3)нахождение характерных линий течения (3.6) и их построение.

Вслучае плоского течения существует функция тока ψ, связанная с проекциями скорости зависимостями:

- в прямоугольных координатах

vx = ∂ψ ∂y ;

v y =−∂ψ ∂x ,

(3.10)

- в полярных координатах

vr = ( ∂ψ / ∂θ) / r ; vθ =−∂ψ ∂r .

(3.11)

Знание функции тока упрощает и нахождение линий тока, так как уравнение их семейства принимает вид

	ψ = С.	(3.12)
Функция тока по проекциям скорости может быть определена? согласно
(3.10), по формуле
y	x
ψ = ∫vx (x, y)dy − ∫(x, y0 )dx +C ,		(3.13)
y0	x0

vk.com/club152685050 | vk.com/id446425943

где x 0 , y0 - координаты точки начала интегрирования. Эта точка выбирается из

удобства интегрирования, обычно начало координат (0; 0). Функцию тока можно определить и следующим образом:

ψ = ∫vx (x, y )dy +C (x ) ,

(3.14)

где С(х) – постоянная интегрирования, но зависящая от х. Для определения С(х) следует продифференцировать выражение (3.14) по х и использовать второе со-

отношение (3.10):	∂	∫	vx (x, y )dy +	∂C(x )	= −vy .
	∂x			∂x

Разность значений функции тока в двух точках (А и В) равна расходу жидкости сквозь цилиндрическую поверхность единичной высоты, проходящую через кривую, соединяющую эти точки:

QAB = ψB −ψA .

(3.15)

Если во всех точках течения отсутствует угловая скорость вращения частиц жидкости ωz = 0 , то такое течение называется безвихревым или потенци-

альным. При этом существует потенциал скорости ϕ - скалярная функция, связанная с вектором скорости зависимостью v = grad ϕ . Проекции скорости:

•	в декартовых координатах -	vx = ∂ϕ ∂x ,	v y = ∂ϕ ∂y ;	(3.16)
•	в полярных координатах -	vr = ∂ϕ ∂r ,	vθ = ( ∂ϕ / ∂θ) / r .	(3.17)
Циркуляция скорости по замкнутому контуру
	Г = ∫vl dl = ∫(vxdx + vydy) ,			(3. 18)

где vl - проекция скорости на касательную к контуру; dl - элемент контура.

При потенциальном течении, в котором потенциал скорости – однозначная функция координат, циркуляция скорости по замкнутому контуру равна нулю.

Во многих реальных вихревых течениях ω ≠ 0 лишь в небольших областях, имеющих вид вихревых шнуров. Вне этих областей поток можно считать потенциальным. Вихревой шнур малых по сравнению с потоком поперечных размеров можно заменить бесконечно тонкой вихревой нитью с интенсивностью I шнура. Согласно теореме Стокса, циркуляция скорости Г по любому контуру, охватывающему вихрь, равна интенсивности вихря:

		Г=I.				(3.19)
Элемент dL вихря интенсивности Г=I индуцирует в любой актуальной
точке жидкости скорость dv	. Согласно формуле Био-Савара,
	dv	=	Г	ω0 ×	r0	dL ,
			4π	r2

где ω0 - орт-вектор угловой скорости, определяющий направление касательной элемента dL вихревой нити; r0 - орт радиус-вектора r , проведенного от dL в

актуальную точку.

Для плоской вихревой нити величина индуцированной скорости v для точки в плоскости вихря определяется интегралом по длине вихря:

Рис. 3.1

vk.com/club152685050 | vk.com/id446425943

v =	Г	∫	sin α	dL ,	(3.20)
	4π
		α r2

очевидно, что sin α есть модуль векторного произведения ω0 ×r0 .

Прямой отрезок вихря, направленный по угловой скорости ω, согласно (3.20) индуцирует скорость

v = 4Гπh (cos α1 −cos α2 ) .

Здесь h - расстояние от точки до отрезка; α1, α2 - углы от отрезка до направлений r1, r2 на точку из начала и конца отрезка.

Для исследования плоских потенциальных потоков наиболее эффективен метод, основанный на использовании функций комплексного переменного:

z = x +iy = reiθ = r(cos θ+i sin θ); i =		.	(3.21)
	−1

Здесь r = x 2 + y 2 и θ = arcsin y / x .

Плоское течение полностью описывается характеристической функцией течения (комплексным потенциалом):

w(z) = ϕ(x, y ) +iψ(x, y ) ,

(3.22)

действительная часть которой представляет собой потенциал скорости, а коэффициент мнимой части – функцию тока. Если течение неустановившееся w=w(z, t), то время t входит в характеристическую функцию как параметр.

Производная комплексного потенциала по z представляет собой комплексную скорость dwdz = vx −iv y . Действительная же скорость в комплекс-

ной форме записывается как v = vx +ivy .

Если течение получено сложением нескольких потенциальных потоков, то может быть использован метод наложения: функция тока, и потенциал скорости результирующего течения определяются как сумма функций тока и потенциалов скорости простейших потоков соответственно:

ψ∑ =ψ1 +ψ2 +ψ3 +...; ϕ∑ = ϕ1 +ϕ2 +ϕ3 +...; w∑ = w1 +w2 +w3 +.... (3.23)

Картину линий тока суммарного течения можно получить графически. Для этого нужно наложить одна на другую сетки линий тока двух составляющих потоков, построенных с одинаковым шагом по расходам: ψ1 = ψ2 = Q1 = Q2

(рис. 3.1). Линии тока суммарного течения будут диагоналями криволинейных параллелограммов, образованных пересечением этих двух сеток.

При использовании метода наложения большое значение имеют так называемые простейшие плоские потоки, для которых ниже при-

ведены комплексный потенциал w, потенциал скорости ϕ и функция тока ψ:

– поступательный поток, текущий со скоростью v∞ под углом α к оси х,

vk.com/club152685050 \| vk.com/id446425943
w = v∞e−iα z ,	ϕ = v∞x x +v∞y y ,	ψ = v∞x x −v∞y y ;	(3.24)

- источник с расходом Q, расположенный в начале координат (для стока Q заменяется на –Q),

w =

ln z ,

ϕ =

ln r = Q ln

x 2 + y 2 ,

ψ =

θ =

arctg

;

(3.25)

2π

- источник с расходом Q , расположенный в точке z0 ,

y − y0

w =

ln(z

−z0 ) ,

ϕ =

ln (x − x 0 )

+( y − y0 )

ψ =

arctg

;

(3.26)

2π

x − x0

- плоский циркуляционный поток – плоский вихрь с циркуляцией Г, расположенный в начале координат,

ψ = − Г

ln r = − Г ln

w =

ln z ,

ϕ =

θ =

arctg

+ y 2

; (3.27)

2πi

2π

- плоский вихрь с циркуляцией Г, расположенный в точке z0 ,

w =

ln(z −z0 ) ,

ϕ =

arctg

y − y0

2πi

2π

x − x0

(3.28)

Г ln (x − x0 )2 + ( y − y0 )2 .

ψ = −

2π

3.2. Примеры решения задач

Задача 3.2.1. Исследовать плоский поток, заданный полем скоростей:

vx = ax 2 ;

vy = −axy .

Построить семейство линий тока, найти расход жидкости через отрезок прямой АВ [А(0,5; 2), В(3; 3)] и вычислить циркуляцию скорости по окружности радиусом R=1,0 c центром в точке С(2; 1).

Решение. 1. Убедимся в возможности существования заданного потока, для чего рассмотрим уравнение неразрывности (3.7):

∂vx ∂x +∂v y ∂y = 2ax −2ax = 0 .

Уравнение неразрывности удовлетворяется, следовательно, существование заданного течения возможно. Поскольку поток плоский (vz = 0 ), по формулам

(3.2)÷(3.5) найдем следующие характеристики:

∂v

∂vy

∂v

(−2ay +0)= −ay -

= 2ax ,

= −2ax ,

∂x

∂y

2 ∂x

∂y

- частицы движутся, растягиваясь по оси х и сжимаясь по оси у с угловыми деформациями;

∂vy

∂v

(−2ay −0)= −ay

ωz

−

- (течение вихревое);

∂x

∂y

vk.com/club152685050 | vk.com/id446425943

dvx

∂vx

+vx

∂vx

+vy

∂vy

= ax

2ax +(−2axy ) 0

= 2a

;

∂t

∂x

∂y

dvy

∂vy

+vx

∂vy

+vy

∂vy

= ax 2 (−2ay ) +(−2axy ) (−2ax ) = 2a2 x 2 y ;

∂x

∂y

∂t

Локальное ускорение ∂

/ ∂t

равно нулю, ибо течение установившееся.

2. Уравнение семейства линий тока (3.6) принимает вид

ax 2

−2axy

После интегрирования и потенцирования

x 2 y = C0 .

Уравнение семейства линий тока может быть найдено и с помощью функции тока, так как течение плоское. Используем формулу (3.13), выбирая в качестве начала интегрирования точку (0; 0):

y	x
ψ = ∫ax 2 dy − ∫−2ax 0 dx +C = ax 2 y +C .
0	0
	Таким образом, уравнение семейства линий
	тока (3.12) (ψ =const) примет вид
	x 2 y = C1.
	Линии тока представлены на рис. 3.2. Так как
	течение установившееся, то траектории совпа-
	дают с линиями тока.
	2. Расход жидкости через отрезок пря-
	мой АВ, согласно (3.15),
Рис. 3.2	QAB = ψB −ψA = axB2 yB −ax A2 y A =	.
Рис. 3.2	= a 32 3 −a 0,52 2 = 26,5a .	.
	= a 32 3 −a 0,52 2 = 26,5a .

3.Циркуляция скорости (3.18) по окружности радиусом R=1,0 с центром

вточке С (2; 1):

3	1	2	0
Г = ∫vx dx +v y dy = ∫ax 2 dx + ∫ax 2 dx _ ∫			(−2xy)dy + ∫	(−2xy)dy = 0.
1	3	0	2

Задача 3.2.2. Два потока – плоский источник производительностью Q, расположенный в начале координат, и поступательный поток со скоростью v∞ ,

параллельный оси х, имеют функции тока
ψ1 =	Q	arctg	y	и ψ2 = v∞ y .
	2π		x

Найти поле скорости течения, образующегося при их наложении, и уравнение линии тока, проходящей через критическую точку К (точку, в которой скорость

равна нулю). Построить графическим методом картину линий тока для

Q = 36 м2/с и v∞ = 3 м/с.

Решение. 1. По формуле (3.23) функция тока суммарного течения

vk.com/club152685050 | vk.com/id446425943

ψ= ψ1 +ψ2 = 2π arctg x + v∞r sin θ

или, после перехода к более удобным полярным координатам (r, θ), по (3.21)

ψ = (Q / 2π)θ+v∞r sin θ.

Проекции скорости по (3.11)

vr =

∂ψ

+v∞ cos θ;

vθ = −

∂ψ

= −v∞ sin θ.

2πr

∂r

r ∂θ

Уравнение семейства линий тока получится из (3.12):

θ+v∞r sin θ = C .

2π

2. Критическую точку К определяем из условий

vθ = vr

= 0 , или

v∞ sin θ = 0 и

+v∞ sin θ = 0.

2πr

Из первого уравнения получаем θ = nπ, а из второго уравнения – r = ±Q / 2πv∞ . По физическому смыслу r может быть величиной только положительной, следовательно, координаты точки К: θ = π и r =Q / 2πv∞ . Если подставим эти ко-

ординаты в уравнение семейства линий тока, то получим постоянную для уравнения линии тока, проходящей через критическую точку К,

С =	Q	π + v∞	Q	sin π =	Q	.
	2π		2πv∞		2

Подставив С в уравнение линий тока, получим искомое уравнение линии тока,

уравнение так называемого «обвода плоского полутела»:	r	=	Q(1 − θ/ π)	.

	пт		2v∞ sin θ

Задавая различные θ, можно вычислить соответствующие им rпт и построить

обвод.

3. Для графического построения (рис. 3.3) нужно построить сетки линий тока складываемых течений. Для первого из них это лучи, исходящие из начала координат,

	arctg	y	= θ = C ,
	arctg		= θ = C ,
		x			1
		x
для второго – прямые, параллельные
оси х,	y = r sin θ = C2 .
Между	двумя соседними							линиями
тока должен быть один и тот же рас-
ход. Поэтому, если провести лучи
через 15°, то в промежутке между
двумя	соседними				линиями тока
будет протекать						Q	= 36 =1,5 м2/c.
		Q =				Q			Рис. 3.3
		Q =							Рис. 3.3
				1	24			24
Исходя из условия					Q2 =			Q1 , соответствующее расстояние между прямыми

vk.com/club152685050 | vk.com/id446425943

y =	Q2	=	1,5	= 0,50	м. Дальнейшее построение понятно из рис. 3.3.
	v∞		3,0

Задача 3.2.3. Характеристическая функция потока задана в виде w = −2 ln(z −2 −i) −1,5i ln(z −2 −i).

Построить линии тока. Найти величину скорости жидкой частицы в точке z=1+i2 и циркуляцию скорости по окружности радиусом R=2,0 с центром в точке А(2; 1).

Решение. 1. Заданную характеристическую функцию представим в виде суммы w1 = −2 ln (z −2 −i) и w2 = −1,5i ln (z −2 −i) .

Сравнивая эти выражения с комплексными потенциалами (3.24)÷(3.28), убеждаемся, что w1 характеризует поток стока с расходом Q=4π, расположенного в

точке z0 =2 +i , а w2 - поток плоского вихря с циркуляцией Г=3π, расположенного в той же точке z0 . Функции тока этих течений получаем выделением мнимых частей w1 и w2 :


			y −1
ψ1	= −2 arctg				и	ψ2 = −1,5 ln	(x − 2) 2 +( y −1) 2	.
			x −2

Уравнение семейства линий тока получится из (3.12):
	-2 arctg	y −1		−1,5 ln		(x −2)2 +( y −1)2 = C .

		x −2

Однако строить линии по этому уравнению весьма затруднительно, поэтому

используем графический метод. Для этого введем новую систему координат
~ ~	с осями, параллельными первоначальной системе, и началом в точке z0 ,
z0 x y
					~	= z −2 −i
следовательно, имеем следующую связь новых и старых координат z						= z −2 −i
~	~
или x	= x −2 и y = y −1. Характеристические функции потока в новой систе-
ме координат имеют вид:		~	и w		~
		~			~
	w = −2 ln z				= −i1,5 ln z ,
	1		~	2	~
соответственно функции тока - ψ1 = −2θ				и	ψ2 = −1,5 ln r .

Для графического построения (рис. 3.4) нужно построить сетки линий тока рассматриваемых течений. Для первого из них это лучи, входящие в начало

	~	~
	y	~
координат z0 : 2 arctg		= 2θ = C1	,	для второго – концентрические окружности
координат z0 : 2 arctg	~	= 2θ = C1	,	для второго – концентрические окружности
	x			~		~		~
с центром в начале координат z0 :				~	= ln	~	2	~	2	= C2	. Между двумя
с центром в начале координат z0 :				ln r	= ln	(x )		+( y )		= C2	. Между двумя

соседними линиями тока должен быть одинаковый расход. Поэтому, если провести лучи через 15°, то в промежутке между соседними линиями тока будет

протекать	Q =	Q	=	4π	= π	м2/c.

	1	24	24		6

Соответствующее расстояние между концентрическими окружностями определяем из условия Q2 = Q1 :

vk.com/club152685050 | vk.com/id446425943

= π/ 6

1,5 ln r2

−1,5 ln r1

или

1,5

После потенцирования получаем

= e

π/ 9

Дальнейшее построение понятно из рис.3.4. Для определения направления результирующего потока по (3.11) найдем скорость от вихря

(vθ )2 = −	∂ψ	2					1
				= −1,5			~ .
	~
~	∂r		(v~ )				r

Окружная скорость					2	совпадает с на-
				θ

правлением θ, т.е. течение вокруг точки z0

происходит против часовой стрелки.

2. Составляющие скорости жидкой частицы в любой точке потока по (3.10):

или	~	= e	π/ 9~
	r2		r1 .

Рис. 3.4

= ∂ψ

= −

2 1

−1,5

2( y −1)

∂y

−1

( x − 2 )

( x − 2 )2 +( y −1)2

− 2

= −

2( x − 2 )

−

1,5( y −1)

= −

2( x −

2 ) +1,5( y −1)

;

+( y −

( x −

2 )

( x − 2 )

+( y −1)

( x − 2 ) +( y −1)

v y

∂ψ

= −

2 1

y −1

+1,5

2( x − 2 )

∂x

y −1

−( x − 2 )2

( x − 2 )2 +( y −1)2

( x −2 )2 +( y −1)2

− 2

= −

2( y −1)

1,5( x −2 )

= − 2( y −1) −1,5( x −2 ) .

( x −2 )2 +( y −1)2

Подставив в эти выражения координаты точки z =1+ i 2,

получим величину

скорости жидкости частицы в этой точке:

= −

2(1−2) +1,5(2 −1)

= 0,25 м/с;

= −

2(1−2) −1,5(2 −1)

= −1,75 м/с;

(1−2)2 +(2 −1)2

v = vx2 +v2y = 0,252 +1,752 =1,77 м/с.

Значение этой скорости можно было найти проще, с помощью (3.11), если те-

~ ~

чение рассматривать в системе координат z0 x y :

1 ∂ψ

= −

;

= −

∂ψ

= −1,5

;

∂θ

∂r

vk.com/club152685050 | vk.com/id446425943

v =

(v~ )2

+(v~

6,25 =

2,5

+ 1,5

Точка z =1+ i 2 имеет следующую полярную координату:

= (x

( y −1)

−2)

(1−2)

+(2

−1)

= 2 .

r =

(x )

+( y )

Таким образом,

v =

2,5 =1,77 м/с.

2 3. Циркуляция скорости по любой окружности с центром в точке А(2; 1),

согласно (3.19), Г=3π.

3.3. Задачи

3-1÷7. Исследовать поток с проекциями скоростей vx и vy (табл. 3.1).

Построить семейство линий тока, вычислить расход жидкости через отрезок АВ и циркуляцию скорости по окружности радиусом R с центром в точке С.

Таблица 3.1

Номер					vx				vy	А(x A ; y A )		В(x B ; yB )		R	С(x C ; yC )
задачи
3-1	3(x			2		− y	2	)	− 6xy	1;	2	2;	3	2,0	0;	0
	3(x					− y		)	− 6xy
3-2	−					2x			2 y	0,5; 1		2,0;	4,0	5,0	2;	6
3-2	−		x		2 + y2				x2 + y2	0,5; 1		2,0;	4,0	5,0	2;	6
			x		2 + y2				x2 + y2
3-3			2x2						− 4xy	0;	0	2;	2	1,0	2;	2
3-4			0,5x						0,5y	2;	1	2;	6	1,5	1,0;	1,2
		x2 + y2
									x2 + y2
									x2 + y2
3-5					3x				-3y	1,0;	1,5	2,0;	3,0	2,0	1;	1
3-6			2х + у						х – 2у	1,0;	1,0	2,0;	2,0	2,0	2,0;	2,0
3-7		0,5х + у							х – 0,5у	2,0;	1,0	2,0;	6,0	2,0	2,0;	3,0

3-8÷13. Исследовать поток, заданный потенциалом скорости ϕ (табл. 3.2). Построить линии тока. Вычислить скорости жидких частиц в точках А и В, расход через отрезок прямой, соединяющий эти точки, и циркуляцию скорости по замкнутому контуру АВС.

									Таблица 3.2
Номер задачи				ϕ		А(x A ; y A )		В(x B ; yB )	С(x C ; yC )
3-8		x	2	− y	2	5; 1		5; 2	0; 0
		x		− y
3-9				2x		2;	1	1; +2	-2; 0
3-9		x2 + y2				2;	1	1; +2	-2; 0
		x2 + y2
3-10	2(x2 − y2 )					1; 2		0; 3	-1; -1
3-11	3arctg (y/x) – y					1;	1	+2; 3	0; -1
3-12	х2 + ху – у2					2,0;	1,0	1,0; 2,0	0; 0
3-13	2х2 + ху – 2у2					1,0;	1,0	2,0; 3,0	3,0; 1,0

vk.com/club152685050 | vk.com/id446425943

3-14÷17. Исследовать поток с функцией тока Ψ (табл. 3.3). Построить семейство линий тока. Найти уравнения линий тока, проходящих через точки А и В, расход жидкости через отрезок прямой АВ, а также циркуляцию скорости по замкнутому контуру АВС.

				Таблица 3.3

Номер задачи	Ψ	А(x A ; y A )	В(x B ; yB )	С(x C ; yC )
3-14	3(х2 – у2)	3; 6	5; 10	6; 1
3-15	у2 + 2ху – х2	2; 4	4; 4	3; 1
3-16	3х2у	1; 2	3; 2	3; 0
3-17	4ху	2; 3	-3; 3	0; 1

3-18÷20. Крыло конечного удлинения заменено П-образным вихрем, лежащим в плоскости хОу (рис. 3.5). Интенсивность вихря Г. Свободные концы вихря простираются в бесконечность. Вычислить вызванные скорости в указанных точках плоскости хОу (табл. 3.4).

	Таблица 3.4

Номер задачи	Расчетные точки
3-18	А(0,5; 0); В(0,75; 0); Е(1,75; 0)
3-19	В(0,75; 0); Д(0,75; 1,45)
3-20	В(0,75; 0); С(0,75; 0,72)

Рис. 3.5

3-21÷26. Течение, полученное от сложения поступательного потока и потока источника, имеет характеристическую функцию w (табл. 3.5). Построить семейство линий тока, найти положение критической точки, составить уравнение линии тока, проходящей через критическую точку. Определить расход жидкости через отрезок АВ.

			Таблица 3.5
		А(x A ; y A )
Номер	w	А(x A ; y A )	В(x B ; yB )
задачи		2; 4
3-21	2 z+1,5ln(z-1)	2; 4	4; 6
3-22	-i 3z+2ln(z-2)	0; 1	-2; 0
3-23	-z+1,5ln(z+i2)	1; 3	2; 5
3-24	3z+2ln(z-0,5)	-2; 3	-3; 4
3-25	i2z+1,5ln(z-i)	1; 5	-1; 6
3-26	-2z+1,5ln(z+1)	2; 4	4; 5

Указание. Используя выражения (3.24), найти величину скорости поступательного потока и его направление, а по (3.25) определить положение источника и его расход. Введя новую систему координат с осями, параллельными

vk.com/club152685050 | vk.com/id446425943

осям системы Оху, и началом в точке расположения источника, задачу решить аналогично примеру 3.2.2.

3-27÷32. Течение от вихреисточника (вихрестока) задано характеристической функцией w (табл. 3.6). Построить линии тока. Найти величину скорости жидкой частицы в точках z1 и z2 , расход жидкости через отрезок прямой, со-

единяющей эти точки, и циркуляцию скорости по окружности радиусом R с центром в точке А.

					Таблица 3.6

Номер	w	z1 = x1 +iy1	z2 = x 2 +iy2	R	А(x A ; y A )
задачи
3-27	-ln(z-i)+2iln(z-i)	3+i2	2-i2	0,5	0; 0
3-28	-ln(z+2)-i2ln(z+2)	2+i3	1-i	3,0	0; 0
3-29	-ln z+i1,5ln z	1+i2	2-i2	2,0	2; 2
3-30	3ln(z+1,5)-i2ln(z+1,5)	-1+i2	i3	3,0	1; 1
3-31	ln(z+i)-2iln(z+i)	1+i3	2	1,0	0; 1
3-32	-ln(z-1,5)+i2ln(z-1,5)	1+i1	-2+i2	2,0	-1; 0

Указание. Задачу решить по аналогии с примером 3.2.3.

3-33÷36. Течение вокруг кругового цилиндра задано характеристической функцией w (табл. 3.7). Построить линию тока, проходящую через точку z=2. Вычислить расход жидкости через окружность радиусом R с центром в начале координат и циркуляцию скорости по этой окружности.

		Таблица 3.7

Номер задачи	w	R
3-33	3ln[(z-1)(z-4)/z]	5,0
3-34	-i3ln[(z-4)/(z-1)]	3,0
3-35	2ln[(z-i)(z-i4)]-2lnz	2,0
3-36	i2[ln(z-i)-ln(z-i4)]	3,0

Указание. Заданную функцию w разложить на части. Используя выражения (3.25)÷(3.28), определить простейшие потоки и найти их функции тока. Произвести аналитически сложение функций тока и получить выражение для функции тока суммарного течения. Для линии тока, проходящей через точку z = 2 , найти постоянную уравнения (3.12). Анализ полученной формулы позволит получить уравнение линии тока.

vk.com/club152685050 | vk.com/id446425943

4.ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ

4.1.Основные сведения из теории, расчетные формулы

иметодические указания

Любая реальная жидкость в той или иной мере обладает свойством вязкости. Однако решение многих важных задач для таких маловязких жидкостей, как вода и воздух, можно получить, считая их невязкими. Причем эти решения во многих случаях подтверждаются экспериментальными данными.

Для решения задачи о движении невязкой жидкости используют уравне-

ние в форме Громеки:	v2
∂v	v2			p
	+grad		+		−U	= −2ω × v ,
	+grad		+		−U	= −2ω × v ,
∂t		2		ρ
∂t		2		ρ

где v, ω - линейная и угловая скорости жидкой частицы; p, ρ - давление и

плотность в рассматриваемой точке; U - потенциал массовых сил (в случае только силы тяжести U = - gz).

Хотя в общем случае уравнение движения не интегрируется, но для частных случаев их интегрирование при некоторых допущениях возможно. Интегралы уравнений движения устанавливают связь между скоростями и давлениями в потоке жидкости.

Для установившегося движения невязкой (идеальной) жидкости (в общем случае вихревого) вдоль линии тока (или вдоль вихревой линии) имеем инте-

грал (уравнение) Бернулли:
	v2	+	p	+ gz = C ,	(4.1)
2			ρ

где константа C постоянна вдоль линии тока.

Уравнение Бернулли является одним из основных в гидрогазодинамике, так как определяет изменение основных параметров течения – давления p, плотности ρ, скорости v и высоты положения z .

Для безвихревого (потенциального) установившегося течения жидкости в

поле только силы тяжести существует интеграл Эйлера:
	v2	+	p	+ gz = C ,	(4.2)
2			ρ

где постоянная С одинакова для всех точек в потоке и определяется из граничных условий (обычно из условия на бесконечности).

Интегралы уравнений движения (4.1) и (4.2) выражают закон сохранения удельной механической энергии. Член v2 / 2 характеризует кинетическую энер-

гию; p/ρ - потенциальную энергию давления, а gz – потенциальную энергию положения.

Интегралы Бернулли и Эйлера используют еще в следующих формах:

ρ	v2	+ p +ρgz = C;	z +	p	+	v	2	= H .	(4.3)
	2			ρg		2g

vk.com/club152685050 | vk.com/id446425943

На основании анализа размерностей следует, что члены уравнения (4.1) характеризуют удельную энергию, отнесенную к единице массы, а (4.3) – удельную энергию, отнесенную соответственно к единице объема и веса.

Составляющие полной энергии или полного напора (4.3) могут взаимопревращаться. Следует иметь в виду, что изменение кинетической энергии несжимаемой жидкости вдоль струйки (потока) не может задаваться произвольно: в соответствии с уравнением неразрывности оно однозначно определяется изменением площади S поперечного сечения канала:

v1S1 = v2 S 2 .

(4.4)

Схема использования интеграла Бернулли следующая. На линии тока выбирают точки 1 и 2, при этом линия тока условно может быть продолжена до точек, где движения жидкости нет. Применив уравнение (4.3) к двум этим точкам, получим

	v2				v2
ρ	1	+ p	+ρgz	= ρ	2	+ p	2	+ρgz	2	.	(4.5)
ρ		+ p	+ρgz	= ρ		+ p		+ρgz		.	(4.5)
	2	1	1		2
	2				2

Для невязкой жидкости характерно постоянство скорости и давления в поперечном сечении потока, поэтому вместо расчетных точек можно рассматривать сечения.

При применении уравнения Бернулли в виде (4.5) в конкретном расчете очень полезны приведенные ниже рекомендации. Сначала следует задать на рисунке два расчетных сечения и плоскость сравнения. В качестве сечений рекомендуется брать:

•свободную поверхность жидкости в резервуаре, где скорость равна ну-

лю, т.е. v=0;

•выход потока в атмосферу, где давление в сечении струи равно давле-

нию окружающей среды, т.е. pабс = pатм или pизб = 0 ;

•сечение, в котором задано или необходимо определить давление (показания манометра или вакуумметра);

•сечение под поршнем, где избыточное давление определяется внешней нагрузкой.

Плоскость сравнения удобно проводить через центр тяжести одного из расчетных сечений, обычно расположенного ниже, тогда геометрические высо-

ты сечений z ≥ 0 .

Далее рекомендуется записать уравнение Бернулли в общем виде (4.5), а затем переписать его, выразив каждый член уравнения через заданные величины и исключив члены, равные нулю. При этом необходимо помнить следующее:

- положительные значения геометрических высот z1, z2 , входящих в пра-

вую и левую часть уравнения, всегда отсчитываются от плоскости сравнения вверх;

- давления p1, p2 должны быть заданы в одной системе отсчета (абсолют-

ной или избыточной); если какое-либо из них задано как вакуумметрическое давление, то его следует выразить через абсолютное давление.

vk.com/club152685050 | vk.com/id446425943

При решении задач по обтеканию тел учитывают граничное условие непротекания жидкости на твердой непроницаемой поверхности, и в первую очередь критические точки, где скорость равна нулю. При этом может быть использован коэффициент давления p (в данной точке), представляющий от-

ношение избыточного (по сравнению с давлением p∞ в невозмущенном потоке) давления p- p∞ к скоростному напору невозмущенного потока ρv∞2 / 2 ,

	p − p∞		v	2
p =

	ρv∞2 / 2	=1−		.
		v∞
В невязкой жидкости коэффициент давления не зависит от рода жидкости

(плотности ρ) и скорости набегающего потока v∞ , являясь функцией лишь безразмерных координат.

4.2. Пример решения задачи

Задача. У фонтана (рис. 4.1) вода вытекает из сопла, имеющего форму конического конфузора длиной l=0,4 м и диаметрами D=120 мм и d=50 мм. Считая воду невязкой жидкостью, вычислить необходимое давление перед соплом для обеспечения заданной высоты H=2,8 м струи.

Дано:

D=120 мм=0,120 м; d=50 мм=0,050 м; l=0,40 м;

H=2,8 м.

Определить: p1 .

Решение. В соответствии с указаниями в п. 4.1 проведем расчетные сечения 1-1 перед соплом и 2-2 на выходе струи в атмосферу, а также плоскость сравнения по сечению 1-1.Составим уравнение Бернулли

= z

Рис. 4.1

ρg

Имеем:

- для сечения 1-1

- для сечения 2-2

z1 = 0;

= l;

= p1 ;

изб

= 0.

изб

Из условия неразрывности (4.4) найдем

= v

(d / D)2 .

Перепишем уравнение Бернулли, выразив входящие в него величины

d 4

= l +

ρg

2g D

откуда получим

vk.com/club152685050 | vk.com/id446425943

= ρg l

(4.6)

D 4

Для определения скорости

напишем уравнение Бернулли вдоль линии

тока АВ:

z A +

= zB +

ρg

Имеем:

z A = l;

zB = l + H ;

p A

= 0;

изб

v A = v2 ;

vB = 0.

Подставив эти величины в предыдущее уравнение, получим

= H .

Из (4.6) найдем искомое давление

0,050

= 30,6 103 Па.

= ρg l

+ H 1

−

=1000 9,81 0,40 +

2,8 1−

D 4

0,120

4.3. Задачи

4-1÷2. Определить скорость воздушного потока (ρв =1,24 кг / м3 ) в от-

крытой рабочей части аэродинамической трубы диаметром d. Спиртовой (ρсп = 820 кг / м3 ) чашечный манометр подсоединен к входному сечению сопла диаметром D и показывает h. Воздух рассматривать как невязкую среду.

К задачам 4-1÷4

4-3÷4. Определить показания чашечного манометра, заполненного водой и подсоединенного к входному сечению сопла размерами D и d аэродинамической трубы, если

скорость воздушного потока (ρв =1,24 кг / м3 )

в открытой рабочей части трубы равна 40 м/с. Воздух рассматривать как невязкую среду.

vk.com/club152685050 | vk.com/id446425943

4-5÷6. Считая жидкость невязкой, определить скорость воды в сечении 1-1 при истечении ее в атмосферу через диффузор. Уровень воды в баке H и избыточное давление pизб =50 кПа постоянны. Отношение диаметров диффузо-

ра d:D=0,80.

4-7÷8. Вода вытекает из бака через диффузор в атмосферу. Пренебрегая потерями, определить, при каком избыточном давлении над свободной поверхностью воды в баке давление в узком сечении 1-1 диффузора станет теоретически равным нулю, если d:D=0,85, а уровень H постоянен?

4-9÷10. Пренебрегая потерями, определить давление в узком сечении 1-1 диффузора при истечении бензина (ρв = 750 кг / м3 ) из бака через диффузор в атмосферу, если уровень бензина в баке H и избыточное давление pизб =24 кПа постоянны, а d:D=0,90.

4-11÷12. Дифференциальный ртутный (ρрт =13,6 103 кг / м3 ) манометр,

присоединенный к установленной горизонтально расходомерной трубе, показывает разницу уровней h. Определить расход воды по трубе, считая ее невязкой, если диаметры расходомерной трубы D и d.

4-13÷14. Какую разность уровней h покажет дифференциальный манометр, заполненный водой, при расходе Q=2,0 м3 / с воздуха (ρв =1,24 кг / м3 )

через расходомерную трубу, если ее диаметры	D и d?
К задачам 4-5÷10	К задачам 4-11÷14

vk.com/club152685050 | vk.com/id446425943

4-15÷16. Необходимо выбрать диаметр входного D сечения аэродинамической трубы (см. рис. к задачам 4-1÷4), если диаметр выходного сечения сопла d, расчетная скорость воздушного (ρв =1,24 кг / м3 ) потока в открытой ра-

бочей части трубы 42 м/с, а избыточное давление при входе в сопло 103 Па. Воздух рассматривать как невязкую среду.

4-17÷18. Из открытого резервуара по трубе переменного сечения вытека-

ет вода в количестве 15 л/с. Определить необходимый напор	H, пренебрегая
потерями, если диаметр входного участка трубы D, а d3 = 50	мм. Найти дав-
ление в точке M, расположенной на оси первого участка трубы.

4-19÷20. Из открытого резервуара по трубе переменного сечения вытекает вода под постоянным напором H. Пренебрегая потерями, определить расход воды, если диаметр второго участка трубы d, а d3 =40 мм. Найти давление

в точке K, расположенной на оси второго участка трубы.

4-21÷22. Для измерения скорости воздушного потока (ρв =1,26 кг / м3 )

использована скоростная трубка с двумя отверстиями – динамическим, расположенным в критической точке K, и статическим - в точке C, где коэффициент давления равен нулю. Определить скорость воздушного потока, если показание дифференциального манометра, присоединенного к ним и залитого водой, равно h.. Воздух рассматривать как невязкую жидкость.

4-23÷24. Для измерения скорости самолета использована скоростная трубка с двумя отверстиями – динамическим, расположенным в критической точке К, и статическим – в точке C, где коэффициент давления равен нулю. Определить показания дифференциального манометра, присоединенного к ним

и залитого ртутью (ρрт =13,6 103 кг / м3 ), если скорость самолета составляет 720 км/ч. Воздух считать невязкой жидкостью с плотностью ρв =1,22 кг / м3 .

К задачам 4-17÷20 К задачам 4-21÷24

vk.com/club152685050 | vk.com/id446425943

4-25÷26. Расход жидкости в трубопроводе измеряется с помощью расходомера Вентури. Показание присоединенного к нему ртутного

(ρрт =13,6 103 кг / м3 ) дифференциального манометра h. Размеры расходомера D и d. Определить расход воды, считая ее невязкой.

4-27÷28. Определить расход воздуха (ρв =1,22 кг / м3 ) в трубопроводе при использовании расходомера Вентури. Показание присоединенного к нему спиртового (ρсп = 820 кг / м3 ) дифференциального манометра h. Размеры расходомера D и d. Воздух рассматривать как невязкую среду.

4-29÷30. Вода вытекает из резервуара по расширяющейся трубе – диффузору в атмосферу. Пренебрегая потерями, определить, при каком уровне воды Н1 в резервуаре давление в узком сечении диффузора станет теоретически рав-

ным нулю, если его размеры D, d, H известны?

4-31÷32. Вода вытекает из резервуара по расширяющейся трубе – диффузору в атмосферу. Уровень воды в резервуаре Н1=1,2 м. Считая жидкость не-

вязкой, определить скорость в узком сечении резервуара, если размеры диффузора D, d, H известны.

4-33÷34. Керосин (ρк = 810 кг / м3 ) вытекает из резервуара по расши-

ряющейся трубе – диффузору в атмосферу. Уровень жидкости в резервуаре Н1=0,8 м. Считая жидкость невязкой, определить давление в узком сечении

диффузора, если его размеры D, d, H заданы.

К задачам 4-25÷28

К задачам 4-29÷34

vk.com/club152685050 | vk.com/id446425943

4-35÷36. Центробежный насос перекачивает воду из открытого резервуара. На какой высоте Н нужно установить насос, чтобы максимальная вакуумметрическая высота на входе в насос не превышала 5 м вод. ст., если подача насоса Q=16,0 л/с и диаметр всасывающего трубопровода d? Гидравлическими потерями пренебречь.

4-37÷38. Центробежный насос установлен на высоте Н над уровнем воды в расходном резервуаре. Пренебрегая гидравлическими потерями, определить вакуум перед входом в насос, если его подача равна Q=30,0 л/с, а диаметр всасывающего трубопровода d.

4-39÷40. При закрытом вентиле ртутный (ρрт =13,6 103 кг / м3 ) манометр показывает h. Определить расход воды, протекающей по трубопроводу диаметром d после открытия вентиля, если показание манометра упало до h2 =520 мм и гидравлическими потерями можно пренебречь.

К задачам 4-35÷38

К задачам 4-39÷40

К задачам 4-41÷42

4-41÷42. Центробежный вентилятор засасывает воздух из атмосферы через трубу. К цилиндрической части трубы, диаметр которой d, присоединена стеклянная трубка, нижним концом опущенная в сосуд с водой. Определить расход засасы-

ваемого воздуха (ρв =1,24 кг / м3 ),

если вода в трубке поднялась на высоту h.

vk.com/club152685050 | vk.com/id446425943

4-43÷44. Найти скорость течения воды в трубе, если показание ртутного (ρрт =13,6 103 кг / м3 ) дифференциального манометра, присоединенного к ди-

намической трубке и к статическому отверстию, равно h. Распределение скоростей по сечению трубы можно считать равномерным.

4-45÷46. Для определения расхода воздуха (ρв =1,26 кг / м3 ) в трубе диаметром D на ее оси установлена динамическая трубка. Найти значение h показания спиртового (ρсп = 800 кг / м3 ) дифференциального манометра при

максимальном расходе Q=70 м3 / с. Распределение скоростей по сечению трубы считать равномерным.

К задачам 4-43÷48

4-47÷48. Трубка Пито установлена на оси газопровода, имеющего диаметр D, по которому перекачивается газ с

удельным весом 10 Н / м3 . Показания спиртового (ρсп = 800 кг / м3 ) диффе-

ренциального манометра h. Считая газ невязкой жидкостью, определить расход газа Q.

4-49÷50. Определить избыточное гидродинамическое давление в носовой точке А тела вращения, движущегося в морской воде (δ =1,02) поступательно с

постоянной скоростью v м/с. Вдали от тела (на бесконечности) жидкость покоится.

4-51÷52. Канал прямоугольного сечения с постоянным уклоном дна имеет местное сужение. Перед сужением ширина канала В1 =12,0 м, глубина по-

тока H, средняя скорость течения воды 0,60 м/с. Пренебрегая потерей напора, определить глубину потока и скорость в узкой части канала шириной

В2 = 6,0 м.

К задачам 4-49÷50

К задачам 4-51÷52

vk.com/club152685050 | vk.com/id446425943

			Исходные данные к задачам гл. 4					Таблица 4.1
			Исходные данные к задачам гл. 4

Номер	D,	d,		h,мм	Номер	D,	d,	h,мм
Задачи	мм	мм		(Н,м)	задачи	мм	мм	(Н,м)
4 - 1	2000	1000		120	4 - 27	400	250	200
4 - 2	2000	1200		140	4 - 28	360	200	180
4 – 3	1800	1000		-	4 - 29	150	100	Н=1,0 м
4 – 4	1700	1000		-	4 - 30	120	80	Н=1,2 м
4 – 5	-	-		Н=5.0 м	4 - 31	140	100	Н=0,9 м
4 – 6	-	-		Н=4,0 м	4 - 32	100	70	Н=1,0 м
4 – 7	-	-		Н=5,2 м	4 - 33	120	90	Н=1,2 м
4 – 8	-	-		Н=4,6 м	4 - 34	120	80	Н=0,9 м
4 – 9	-	-		Н=4,8 м	4 - 35	-	80	-
4 – 10		-		Н=4,0 м	4 - 36	-	100	-
4 – 11	250	100		700	4 - 37	-	100	Н=4,0 м
4 – 12	240	120		500	4 - 38	-	90	Н=4,2 м
4 – 13	500	200		-	4 - 39	-	80	550
4 – 14	400	200		-	4 - 40	-	75	560
4 – 15	-	-		-	4 - 41	-	200	140
4 – 16	-	-		-	4 - 42	-	180	120
4 – 17	180	-		-	4 - 43	-	-	300
4 – 18	160	-		-	4 - 44	-	-	320
4 – 19	-	75		Н=2,5 м	4 - 45	150	-	-
4 – 20	-	80		Н=2,4 м	4 - 46	160	-	-
4 – 21	-	-		100	4 - 47	400	-	36
4 – 22	-	-		120	4 - 48	360	-	40
4 – 23	-	-		-	4 - 49	v=9,0 м/c
4 – 24	-	-		-	4 - 50	v=10,0м/c
4 – 25	120	75		300	4 - 51	-	-	Н=3,0 м
4 – 26	120	80		240-	4 - 52	-	-	Н=2,8 м

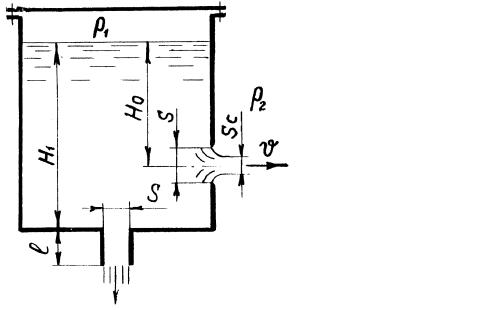
vk.com/club152685050 | vk.com/id446425943

5. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ, НАСАДКИ И ГИДРОАППАРАТЫ

5.1.Основные сведения из теории, расчетные формулы

иметодические указания

Истечение через малые отверстия в тонкой стенке. Отверстие принято считать малым, если его диаметр d весьма мал по сравнению с напором Н. Под термином «тонкая» стенка следует понимать такую, толщина которой не превышает диаметра отверстия.

На расстоянии l (0,5 – 1,0)d от плоскости отверстия образуется так называемое сжатое сечение струи (рис.5.1). Площадь сжатого сечения S c = εS ,

где S –площадь отверстия; ε - коэффициент сжатия.

Скорость v в сжатом сечении и расход жидкости Q определяются форму-

лами:

v = ϕ	2gH ;			(5.1)
Q = μS			,	(5.2)
		2gH

где ϕ - коэффициент скорости, характе-

ризующий уменьшение действительной скорости v по сравнению со скоростью невязкой (идеальной жидкости); μ = εϕ -

коэффициент расхода; H – расчетный напор, который в общем случае равен сумме геометрического и пьезометрического напоров, т.е.

H = H 0	+	p1 − p2	.	(5.3)

		ρg

Если истечение происходит из закрытого резервуара в атмосферу, числитель вто- Рис.5.1

рого слагаемого (5.3) представляет избыточное давление на поверхности жидкости в резервуаре; при истечении в атмосферу из открытого резервуара второе слагаемое обращается в нуль.

Численные значения ϕ, μ и ε зависят от числа Рейнольдса. Для маловязких жидкостей (вода, бензин, керосин), истечение которых обычно происхо-

дит при достаточно больших числах Рейнольдса (Re > 105 ), коэффициенты ис-

течения меняются в сравнительно небольших пределах, поэтому в расчетах

можно	пользоваться их средними для отверстия значениями
ε = 0,64;	ϕ = 0,97; μ = 0,62 .

Если боковые стенки резервуара или трубы находятся на расстоянии менее трех диаметров от оси отверстия (рис.5.2), то их направляющее действие уменьшает степень сжатия струи ( ε увеличивается). Для круглого отверстия

vk.com/club152685050 | vk.com/id446425943

площадью S при истечении из цилиндрического ре-

зервуара или трубы площадью S1 , коэффициент сжатия струи можно определять по формуле

ε = 0,64 + 0,36(S / S1 )2 .

При истечении жидкости в жидкую среду, например, в сообщающихся сосудах (истечение под уровень или через затопленное отверстие), скорость

Рис. 5.2 истечения v и расход жидкости Q рассчитываются по тем же формулам (5.1) и (5.2), но в этом случае для расчетного напора H величинаH 0 представляет собой разность уровней в сосудах. Значения коэффици-

ентов истечения для затопленных отверстий можно принимать такими же, как и в случае истечения в газовую среду.

Истечение через насадки. Насадком называют короткие трубки (патрубки) длиной (2–6) d, применяемые для улучшения процесса истечения жидкости. При этом скорость и расход определяются по формулам (5.1) и (5.2), но со своими коэффициентами ϕ и μ.

Заметим, что для вертикально расположенных насадков при определении расчетного напора необходимо учитывать их длину. Так, для случая на рис. 5.1 имеем

H = H1 + l + ( p1 − p2 ) / ρg .

Одним из наиболее распространенных является внешний цилиндрический насадок (рис. 5.3), для которого в приближенных расчетах, обычно, при-

нимают ϕ=μ=0,82, ε=1,0.

Благодаря наличию сжатого сечения, внутри насадка образуется вакуум, величина которого характеризуется вакуумметрической высотой hвак ≈ 0,75 H . Предельная величи-

	на вакуума в сжатом сечении ограничена значе-
	ниями атмосферного давления pатм и давления на-
	сыщенных паров		pн.п, которое зависит от рода
	жидкости и температуры. При значениях H, близ-
	ких к	H пред =	hвак.пред	=	p	атм	− p	н.п	,
			0,75
						0,75ρg
Рис.5.3	нарушается сплошность движения, внутри насадка
	возникает кавитация. При				H > H пред происходит

срыв потока – струя отрывается от внутренней поверхности насадка, истечение будет происходить так же, как и через отверстие в тонкой стенке.

Истечение при переменном напоре. Расчет опорожнения и заполнения емкостей, судовых отсеков и цистерн, площадь горизонтальных сечений которых велика по сравнению с площадью перепускных отверстий, арматуры производится без учета сил инерции в резервуарах и перепускных устройствах. Процесс истечения за бесконечно малый промежуток времени рассматривается

vk.com/club152685050 | vk.com/id446425943

как установившийся. Мгновенный расход Q определяется при этом по формуле

Q = μS 2g(h + ( p1 − p2 ) / ρg) ,

где μ - коэффициент расхода выпускного устройства, отнесенный к площади S выходного отверстия. Вместо μ может быть использован коэффициент по-

терь	напора ζ	на выпускном устройстве
μ =1/	ζ ; p1, p2	- давление в резервуаре и в про-

странстве, куда происходит истечение жидкости

(рис. 5.4).

Для маловязких жидкостей коэффициенты μ и ζ можно принимать постоянными в течение всего процесса. Тогда время частичного опорожнения сосуда от начального условия H1 до уровня H определится по формуле

Ω(h)dh

t =

∫

μS 2g

h + ( p − p ) / ρg

где Ω(h) - площадь

поверхности

жидкости в

Рис.5.4

резервуаре.

Ω(h) = Ω = const , при по-

Для призматического резервуара, у которого

стоянстве p1 − p2 будем иметь

t =

2Ω

H1 +

− p

− H

p − p

μS

ρg

Время полного опорожнения резервуара в этом случае получим, приняв H=0. Истечение через гидроаппараты. В этом случае истечение всегда про-

исходит в среду, заполненную той же самой жидкостью (истечение под уровень). При этом энергия, теряемая на вихреобразования, может быть учтена коэффициентом расхода μ. Поэтому расход Q жидкости через гидроаппараты (дроссели и клапаны) рассчитывают по формуле

Q = μS	2 p / ρ ,
где S - площадь проходного сечения;	p - перепад давления на рассматривае-

мом элементе; ρ - плотность жидкости.

Указания к решению задач:

-при решении задач, рассматривающих работу гидроцилиндра, необходимо использовать уравнение равновесия поршня: сумма всех сил, приложенных к нему, равна нулю;

-жидкость считать несжимаемой, а движение поршня - равномерным;

-утечками и трением в цилиндре, а также весом поршней и штоков пренебречь;

vk.com/club152685050 | vk.com/id446425943

- расход через последовательно соединенные элементы один и тот же, а при разделении потока его расход равен сумме расходов в ответвлениях.

Следует иметь в виду, что в гидроцилиндре с односторонним штоком изза наличия штока расход жидкости по разные стороны поршня будет различным:

Q1 = vпπD2 / 4 - со стороны поршневой полости;

Q2 = vпπ(D2 − Dшт2 ) / 4 - со стороны штоковой полости.

Здесь vп - скорость движения поршня; D и Dшт - диаметры поршня и штока.

5.2. Примеры решения задач

Задача 5.2.1. Бак разделен на две секции переборкой, в которой имеется отверстие с острой кромкой (рис. 5.5). В левую секцию поступает вода в количестве Q=50 л/с. Из каждой секции вода вытекает через внешний цилиндрический насадок. Диаметры насадок и отверстия в переборке одинаковы и равны

60 мм.

Определить расход воды через каждый насадок , полагая отверстие в переборке затопленным, а уровни воды в обоих секциях постоянными.

Дано: Q=50 л/с=0,050 м3 / с;

d=60 мм=0,060 м.

Определить: Qл , Qп .

Решение. 1. Из условия постоянства

уровня Н имеем: расход через правый наса-

док

Qп

должен равняться расходу через от-

верстие, т.е. Qп =Q0 или

πd22

2gH 2 = μ0

πd

2gH ,

(5.4)

где μ0 , μн - коэффициенты расхода через

отверстие и внешний цилиндрический наса-

док.

2. Из условия

постоянства

уровней воды

Рис.5.5

следует, что

πd 2

Q = Qл

+ Qп

= μн

2g( H +

H 2 ) + μн

2gH 2 .

(5.5)

3. Из (5.4) имеем

H = H 2μн2 / μ02 . Подставим Н в (5.5):

πd

+ H

+ μ

πd

= Q .

2g H

μн

2gH

μ0

Отсюда находим выражение для напора H 2 :

H 2 =

16Q2

μн2 π2 d 4 2g

( μн2 / μ02 +1 +1)2

vk.com/club152685050 | vk.com/id446425943

Полагая μ0 =0,62			и μн=0,82, получим						H = 3,36 0,822 / 0,622 = 5,88 м;
H 2 =								16 0,050	2						= 3,36 м.
H 2 =		2	3,14	2	0,060		4			2			2	2	= 3,36 м.
0,82		2		2			4		0,82	2	/ 0,62		2	2
0,82								2 9,81	0,82		/ 0,62			+1 +1

4. Используя выражения для расхода через левый и правый насадки, бу-
дем иметь
Qл = 0,82	3,14 0,0602					2 9,81 (5,88 + 3,36)= 0,312 м3 / с = 31,2 л / с;
Qл = 0,82						2 9,81 (5,88 + 3,36)= 0,312 м3 / с = 31,2 л / с;
			4
Qп = 0,82 3,14 0,0602						2 9,81 3,36 = 0,0188 м3 / с =18,8 л / с.
Задача 5.2.2.			4									элемент 1 редукционного
Задача 5.2.2.			Сила давления на подвижный									элемент 1 редукционного

клапана (рис. 5.6), применяемого для понижения давления на некотором участке гидросистемы, определяется выражением F = p2 πD 2 / 4 . Найти редуцированное давление p2 , которое будет иметь место при расходе жидкости через

клапан	Q=0,6 л/с, если		давление на входе в клапан p1 =10,0МПа. Вычислить
для этого случая зазор			y клапана, приняв его коэффициент расхода μ=0,60.
Жесткость пружины			С=235				Н/мм, ее сжатие l=2,0 мм. Диаметр клапана
D=10 мм. Плотность жидкости ρ = 900 кг / м3 .
Дано: p =10,0 МПа=10,0 106 Па;
	1
	Q=0,6 л/с =0,6 10−3 м3/с;
	С=235 Н/мм=235 103 Н / м;
	l=2,0 мм=2,0 10−3 м;
	ρ = 900 кг / м3 .
Определить: y.								1
Решение. 1.Так как давление p1 действу-								1
Решение. 1.Так как давление p1 действу-
ет одинаково на левую и правую часть подвиж-
ного элемента 1, то условие							его равновесия		Рис.5.6
запишется в виде F		= cl = p				2	πD2 / 4 .
	пр					2
Откуда p2 =		4cl		=	4 235 103 2,0 10−3			= 6,0 106 Па=6,0 МПа.
Откуда p2 =				=				= 6,0 106 Па=6,0 МПа.
		πD 2					3,14 0,0102
2. Расход жидкости через щель клапана площадью S будет									определяться выра-
жением
				Q = μS 2( p1 − p2 ) / ρ .					(5.6)
Учитывая, что S= πDy , из (5.6) получим
y =	Q	=					0,6 10−3		= 0,34 10−3м
μπD	2( p1 − p2 ) / ρ		0,60 3,14 0,010 2(10,0 − 6,0) 106						/ 900
= 0,34мм.

vk.com/club152685050 | vk.com/id446425943

	5.3. Задачи
К задачам 5-1÷2	5-1÷2.	В вертикальной стенке, разде-
	ляющей бак на две части, расположено круг-
	лое отверстие	диаметром d на высоте Н. В

его левой замкнутой части уровень воды h, показание манометра pм , а расход через от-

верстие Q=3,1 л/с.

Определить уровень воды h2 в правой секции, диаметр донного отверстия d2 и скорость v2 в сжатом сечении струи, вытекаю-

щей из бака. Напоры в обеих секциях считать постоянными.

5-3÷4. Определить, пренебрегая потерями напора, начальную скорость истечения жидкости из сосуда, заполненного слоями воды и масла (относительная плотность δ=0,80) одинаковой высоты h.

Найти начальную скорость истечения при заполнении сосуда только водой или только маслом до уровня 2h.

5-5÷6. Определить расход воды Q через отверстие с острой кромкой диаметром d, выполненное в торце трубы диаметром D, если показание манометра перед отверстием pм и высота расположения манометра над осью трубы

h. Как изменится расход, если к отверстию присоединить цилиндрический насадок? Давление на выходе из насадка атмосферное.

К задачам 5-3÷4

К задачам 5-5÷6

5-7÷8. В бак, разделенный на две секции переборкой, имеющей отверстие диаметром d с острой кромкой поступает вода в количестве Q=75л/с. Из каждой секции она вытекает через цилиндрический насадок. Диаметр насадка, присоединенного к правой секции, равен диаметру отверстия. Предполагая, что отверстие в переборке затоплено, а режим истечения установившийся, опреде-

vk.com/club152685050 | vk.com/id446425943

лить диаметр насадка левой секции, чтобы расходы через оба насадка стали равными.

Указание. Использовать рис. 5.5, предполагая диаметр насадка левой секции неизвестным.

5-9÷10. В бак, разделенный перегородкой на два отсека, подается керосин в количестве Q=4,0 л/с. В перегородке имеется цилиндрический насадок, диаметр которого D. Керосин из второго отсека через отверстие диаметром d вытекает наружу, в атмосферу. Определить высоты H1, H 2 уровней керосина,

считая их постоянными.

5-11÷12. В резервуар А подается вода, откуда через сопло диаметром D перетекает в резервуар Б. Далее через цилиндрические насадки вода попадает в резервуар В и, наконец, вытекает в атмосферу. Диаметры насадок соответственно d1=10 мм и d2 =6 мм, а длина l=25 мм. Высота уровня воды в резер-

вуаре В равна Н. Определить расход воды через систему и перепады уровней h1 и h2 , предполагая режим установившимся. Коэффициент расхода сопла

принять μ=0,97.

К задачам 5-9÷10

К задачам 5-11÷12

К задачам 5-13÷14

5-13÷14. Определить избыточное давление в отсеке, затопляемом забортной водой через

кингстон А площадью S1 = 0,1 м2 с коэффициен-

том местной потери напора ζ1 = 2 для положения, когда уровни воды сна-

ружи ζ1 = 2 и внутри отсека соответственно рав-

ны H и h. Воздух вытесняется через круглое отверстие диаметром d. Сжимаемость воздуха не

учитывать, т. е. полагать ρ =1,23 кг / м3 =const.

vk.com/club152685050 | vk.com/id446425943

5-15÷16. Прямоугольный тонкостенный понтон размерами L=5 м, В=2м и Н имеет массу, соответствующую начальной осадке T 0 =0,15 м, и находит-

ся на плаву без крена и дифферента. Определить время полного затопления (Т=Н ) с момента открытия в днище понтона отверстия диаметром d.

5-17÷18. Определить время опорожнения резервуара диаметром D с вертикальной осью через донное круглое отверстие, диаметр которого d. Начальный уровень жидкости Н, избыточное давление над ней pм =const. Как изме-

нится время опорожнения, если: а) pм =0; б) pм =0 и к отверстию присоединить внешний цилиндрический насадок длиной 250 мм?

5-19÷20. Отсек судна с сечением, изображенном на рисунке, длиной L=10,0 м при гидравлических испытаниях заполнен водой под давлением pм .

Определить время опорожнения отсека через донное отверстие диаметром d, если одновременно будет открыт обратный клапан К. Как изменится время опорожнения, если над поверхностью воды в отсеке поддерживать постоянное избыточное давление pм ?

5-21÷22. Гидравлическое реле времени состоит из цилиндра, в котором помещен поршень со штоком-толкателем. Диаметр поршня - D, а штока - Dш .

Цилиндр присоединен к емкости с постоянным уровнем Н жидкости. Под действием давления, передающегося из емкости в правую полость цилиндра, поршень перемещается, вытесняя жидкость из левой полости в ту же емкость через

трубку и дроссель с площадью проходного сечения S0 = 25 мм2 .

Вычислить время срабатывания реле, определяемое перемещением поршня на расстояние l=100 мм из начального положения до упора в торец цилиндра. Коэффициент расхода дросселя принять μ=0,65. Потерями в трубке, кроме потерь напора на дросселе, пренебречь.

К задачам 5-19÷20

К задачам 5-21÷22

vk.com/club152685050 | vk.com/id446425943

5-23÷24. Определить скорость перемещения гидротормоза диаметром D, нагруженного силой F, если перетекание жидкости (относительная плотность δ = 0,90 ) из нижней полости цилиндра в верхнюю происходит через два отверстия диаметром d. Коэффициент расхода μ принять как для отверстия в тонкой стенке. Давление жидкости над поршнем не учитывать.

К задачам 5-23÷24

5-25÷26. Определить скорость поршня гидроцилиндра при движении против нагрузки F. Давление на входе в дроссель ДР pн , на сливе

pс =0,30МПа.

Диаметры: поршня D, штока Dш , отверстия дросселя d. Коэффициент расхода дросселя принять μ=0,62. Рабочая жидкость – масло (ρ = 900 кг / м3 ).

5-27÷28. Определить площадь проходного сечения дросселя ДР, установленного на сливе гидроцилиндра, при условии движения штока цилиндра под действием внешней нагрузки F со скоростью vп =100 мм/с. Диаметры: поршня

D, штока Dш . Избыточное давление на сливе pм . Коэффициент расхода дросселя принять μ=0,65. Рабочая жидкость – масло (ρ = 850 кг / м3 ).

К задачам 5-25÷26

К задачам 5-27÷28

vk.com/club152685050 | vk.com/id446425943

5-29÷30. Определить скорость движения поршня диаметром D под действием силы F на штоке диаметром Dш . Проходное сечение дросселя ДР

S0 = 2,0 мм2 , его коэффициент расхода μ=0,75, избыточное давление слива pс = pм. Давление в штоковой части цилиндра принять равным нулю, потерями давления от гидроцилиндра до дросселя пренебречь. Рабочая жидкость – масло (ρ = 900 кг / м3 ).

5-31÷32. Рабочая жидкость (ρ = 850 кг / м3 ) подается от насоса в гидро-

цилиндр, а затем через два отверстия диаметром d в поршне и гидродроссель ДР на слив. Определить площадь проходного сечения дросселя для случаев:

- поршень находится в неподвижном равновесии под действием силы F; - поршень перемещается со скоростью vп =10 мм/с влево против нагруз-

ки F. Диаметры: поршня D, штока Dш . Давление насоса pн , давление на сливе pс =0. Коэффициент расхода принять для отверстия в поршне μ0 =0,80, а дросселя μдр=0,65.

5-33÷34. Правая и левая полости цилиндра гидротормоза сообщаются между собой посредством рабочей жидкости (ρ = 900 кг / м3 ) через дроссель ДР с проходным отверстием диаметра d и коэффициентом расхода μ=0,65. Определить скорость перемещения поршня размерами D и Dш под действием силы F, учитывая потери давления в гидролинии только на дросселе.

К задачам 5-29÷30

К задачам 5-31÷32

К задачам 5-33÷34

vk.com/club152685050 | vk.com/id446425943

5-35÷36. Жидкость плотностью ρ = 850 кг / м3 подается от насоса через дроссель ДР в гидроцилиндр, а затем через четыре отверстия диаметром d на

слив. Определить площадь проходного	сечения дросселя, если поршень дви-
жется против нагрузки F со скоростью	vп =4,0 см/с. Диаметры: поршня D,

штока Dш . Давление насоса pн , давление на сливе pс =0. Коэффициенты расхода принять для отверстия в поршне μ0 =0,82, а для дросселя μдр=0,60.

5-37÷38. Рабочая жидкость (ρ = 850 кг / м3 ) подводится в поршневую полость гидроцилиндра под давлением pн . На линии слива установлен дрос-

сель ДР с проходным отверстием диаметром d и коэффициентом расхода μ=0,65. Давление на сливе pс =0,10 МПа, усилие на штоке F. Диаметры: порш-

ня D, штока Dш . Определить скорость перемещения поршня. Каким должен быть диаметр сечения дросселя (при μ=0,65), чтобы скорость поршня стала равной vп =5,0 см/с?

5-39÷40. На рисунке показана упрощенная схема самолетного гидропневмоамортизатора. Процесс амортизации при посадке самолета происходит

за счет проталкивания рабочей жидкости (ρ = 900 кг / м3 ) через отверстие диаметром d (коэффициент расхода μ=0,75) и за счет сжатия воздуха. Диаметр поршня D. Определить скорость движения цилиндра относительно поршня в начальный момент амортизации, когда давление воздуха в верхней части амортизатора pм , расчетное усилие F.

К задачам 5-35÷36

К задачам 5-37÷38

К задачам 5-39÷40

vk.com/club152685050 | vk.com/id446425943

		Исходные данные к задачам гл. 5					Таблица 5.1
		Исходные данные к задачам гл. 5

Номер	D, мм	Н, м	d, мм	h, м	pм ( pн )	F, кН		Dш , мм
задачи					МПа
5-1	-	1,0	50	2,5	0,010	-		-
5-2	-	1,2	50	2,4	0,012	-		-
5-3	-	-	-	1,25	-	-		-
5-4	-	-	-	1,00	-	-		-
5-5	200	-	120	1,3	0,100	-		-
5-6	200	-	100	1,2	0,120	-		-
5-7	-	-	100	-	-	-		-
5-8	-	-	80	-	-	-		-
5-9	60	-	50	-	-	-		-
5-10	60	-	40	-	-	-		-
5-11	8,0	1,1	-	-	-	-		-
5-12	10,0	1,4	-	-	-	-		-
5-13	-	2,5	100	1,1	-	-		-
5-14	-	3,0	110	1,2	-	-		-
5-15	-	1,0	100	-	-	-		-
5-16	-	1,2	110	-	-	-		-
5-17	1,0	5,0	50	-	0,098	-		-
5-18	1,2	4,8	40	-	0,080	-		-
5-19	-	5,0	100	-	0,098	-		-
5-20	-	4,6	90	-	0,080	-		-
5-21	80	0,90	-	-	-	-		40
5-22	70	1,00	-	-	-	-		30
5-23	200	-	10,0	-	-	120		-
5-24	100	-	6,0	-	-	40		-
5-25	70	-	1,2	-	20,0	55		30
5-26	80	-	1,0	-	16,0	70		40
5-27	80	-	-	-	0,30	60		40
5-28	70	-	-	-	0,20	50		30
5-29	80	-	-	-	0	10		30
5-30	140	-	-	-	0,10	20		60
5-31	100	-	2,0	-	1,20	3		80
5-32	80	-	1,6	-	0,80	2,6		40
5-33	140	-	5,0	-	-	15		60
5-34	100	-	4,6	-	-	10		60
5-35	100	-	1,5	-	1,00	3,2		80
5-36	100	-	2,0	-	1,40	3		50
5-37	140	-	2,0	-	8,00	90		70
5-38	125	-	1,8	-	6,00	70		60
5-39	100	-	8,0	-	0,200	50		-
5-40	80	-	8,0	-	0,180	40		-

vk.com/club152685050 | vk.com/id446425943

6. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

6.1.Основные сведения из теории, расчетные формулы

иметодические указания

По способам гидравлического расчета трубопроводы делятся на простые и сложные. Простым называется трубопровод, состоящий из одной линии труб постоянного или переменного сечения без ответвлений. Отличительной особенностью простого трубопровода является постоянство расхода в любом сечении по всей его длине. Сложным называется трубопровод, содержащий какоелибо ответвление (параллельное соединение труб или разветвление). Всякий сложный трубопровод можно рассматривать как совокупность нескольких простых трубопроводов, соединенных между собой параллельно или последовательно. Поэтому в основе расчета любого трубопровода лежит задача о расчете простого трубопровода.

Движение жидкости в напорных трубопроводах происходит благодаря тому, что ее энергия (напор) в начале трубопровода больше, чем в конце. Этот перепад уровней энергии создается различными способами: работой насоса, за счет разности уровней жидкости, давлением газа и пр.

Основными расчетными соотношениями для простого трубопровода являются:

- уравнение Бернулли, устанавливающее соотношение между удельными (отнесенными к единице веса) энергиями жидкости в двух сечениях потока:

+ ∑h 1−2 ;

z1 +

+ α1

= z2

+ α2

(6.1)

ρg

- уравнение расхода:

Q=const (вдоль потока) или v1S1 = v2 S2 ;

(6.2)

- формулы для расчета потерь напора на трение по длине трубы и в мест-

ных сопротивлениях:

l v2

дл

= λ

= ζ

(6.3)

d 2g

которые после выражения скорости v через расход Q ( v = 4Q									π d 2 ) принимают
вид			l 8Q2			8Q2
h	дл	= λ	l 8Q2		и h = ζ	8Q2		.	(6.4)
h		= λ			и h = ζ			.	(6.4)
			d gπ2 d	4	м	gπ2 d	4
			d gπ2 d	4		gπ2 d	4
В формулах (6.1) - (6.4):

z1 и z2 - геометрические высоты центров тяжести сечений над произвольной горизонтальной плоскостью сравнения; p1 и p2 - давления в центрах тяжести сечений; v1 и v2 - средние скорости в сечениях; α1 и α2 - коэффициенты кинетической энергии в сечениях (расчетные значения для потока в круглой трубе: α=2 - при ламинарном режиме, α =1 - при турбулентном); S1 и S2 - площади

vk.com/club152685050 | vk.com/id446425943

сечений; ρ - плотность жидкости; ∑h1−2	- суммарная потеря полного напора
на пути от первого до второго сечения; l	и d - длина и диаметр трубы; λ - ко-

эффициент гидравлического трения; ζ - коэффициент местного сопротивления. Использование формул (6.3) связано с выбором коэффициентов гидравлического трения λ и местных сопротивлений ζ. Расчетные значения этих величин, а также коэффициенты кинетической энергии α , зависят от режима тече-

ния жидкости.
Для определения режима необходимо найти число Рейнольдса:
Re = vd	=	4Q	(6.5)
Re = vd	=	πdν	(6.5)
ν		πdν

(здесь ν - кинематический коэффициент вязкости жидкости) и сравнить его с критическим значением Reкр=2300. Если Re ≤ Reкр, то режим течения лами-

нарный; при Re > Reкр - режим турбулентный.

Ниже приведены расчетные формулы для коэффициента гидравлического трения λ при различных режимах течения.

При ламинарном режиме λл однозначно зависит от числа Рейнольдса:

λл = f (Re) = 64 Re .	(6.6)
При турбулентном режиме λт в общем случае зависит от числа Рей-
нольдса Re и относительной шероховатости	/ d : λт =ƒ( Re, / d ). Здесь -

эквивалентная абсолютная шероховатость стенок трубы. Универсальной формулой, учитывающей одновременно оба фактора, является формула Альтшуля:

	68	+		0,25	(6.7)
λт = 0,11		+		.	(6.7)
Re			d

При малых значениях Re и / d (Re<20d/ ) (6.7) обращается в формулу Блазиуса для так называемых гидравлически гладких труб:

λт =	0,316 .	(6.8)
	4 Re

Наоборот, при больших Re и / d (6.7) принимает вид формулы Шифринсона для зоны квадратичного сопротивления:

		0,25	(6.9)
	λт = 0,11	.	(6.9)
	d
Для удобства пользования формулой Альтшуля в прил. 5 приведен гра-
фик λт =ƒ	(Re, / d ).

Значения коэффициентов местных сопротивлений ζ в общем случае определяются геометрической формой сопротивления и величиной числа Рейнольдса. При ламинарном режиме коэффициент ζ зависит от обоих этих факторов, а при турбулентном режиме - только от формы местного сопротивления. Численные значения коэффициентов ζ находят в справочной литературе. При подсчете местных потерь по формуле (6.3) следует обращать внимание на ука-

vk.com/club152685050 | vk.com/id446425943

зания, к какой скорости (до или после сопротивления) отнесены коэффициенты ζ. В задачах данного сборника коэффициенты ζ обычно заданы или приведены в приложении и отнесены к скорости после местного сопротивления. Исключение составляет коэффициент ζвых (выход из трубы в резервуар), который отне-

сен к скорости перед местным сопротивлением.

Как указано ранее, решение задач данного раздела связано с использованием уравнения Бернулли (6.1). При его применении в конкретном расчете необходимо учитывать приведенные в п. 4.1 рекомендации.

К ним необходимо добавить следующее:

- суммарную потерю напора ∑h1−2 следует представить подробно в виде

суммы потерь на трение по длине и местных потерь, определяемых формулами

(6.3) или (6.4).

Для удобства расчетов введем понятие расчетного напора:
H = z − z	2	+	р1− р2	.	(6.10)

1			ρg

Расчеты простых трубопроводов сводятся к трем типовым задачам: определению напора (или давления), расхода и диаметра трубопровода. Далее рассмотрена методика решения этих задач для простого трубопровода постоянного сечения.

Задача I. Дано: размеры трубопровода l и d, шероховатость его стенок , свойства жидкости (ρ, ν), расход жидкости Q.

Определить: требуемый напор H (одну из величин, определяющих на-

пор).

Решение.

1. Составляется уравнение Бернулли с учетом приведенных рекоменда-

ций.

2. Уравнение решается относительно H.

Полученная расчетная формула содержит неизвестный коэффициент λ .

3.По формуле (6.5) определяется Re и устанавливается режим движения.

4.Находится значение λ по формуле (6.6) или (6.7) в зависимости от режима движения.

5.По формуле, полученной в пункте 2, определяется H и по (6.10) искомая величина.

Задача II. Дано: размеры трубопровода l и d, шероховатость его стенок

,свойства жидкости (ρ, ν), напор H. Определить расход Q.

Решение.

1. Составляется уравнение Бернулли с учетом приведенных рекоменда-

ций.

2. Уравнение решается относительно искомой величины Q. Полученная формула содержит неизвестный коэффициент λ, зависящий от Re. Непосредственное нахождение λ в условиях данной задачи затруднено, так как при неизвестном Q не может быть заранее установлено Re. Поэтому дальнейшее решение задачи выполняется методом последовательных приближений.

vk.com/club152685050 | vk.com/id446425943

3. Задается режим течения. Это можно сделать, основываясь на вязкости жидкости (вода, бензин, керосин, дизельное топливо - турбулентный режим; масло, нефть - ламинарный), но с последующей проверкой по результатам расчета. Можно также режим течения определить сразу однозначно, сравнивая расчетный напор Н с его критическим значением

H кр ≈	32ν2l	Reкр .	(6.11)
	gd 3

Если Н<H кр , то режим - ламинарный. При Н>H кр режим - турбулентный. 4. При ламинарном режиме расход определяется из формулы

H =	16Q2	λл	L	=	128νL		Q	,	(6.12)
	2gπ2 d 4		d			πgd 4

где L=l + ∑lэкв − приведенная длина трубопровода;									lэкв −эквивалентные дли-

ны местных сопротивлений при ламинарном режиме. В учебных задачах последние даются, как правило, в долях длины трубопровода.

Проверяется режим течения.

В случае турбулентного режима определяется значение λI по формуле

(6.9), полагая в первом приближении течение в зоне квадратичного сопротивления. Если сведения о шероховатости отсутствуют (заданы гидравлически гладкие трубы), то значение λI можно задать, например, λI =0,03. Принимая во

внимание, что этот коэффициент изменяется в сравнительно узких пределах, большой ошибки при этом не будет.

5. Определяется QI =ƒ( λI ) в первом приближении по формуле, полученной в пункте 2.

6. Находится Re I =ƒ(QI ) в первом приближении и определяется режим движения жидкости.

7.Уточняется значение λII во втором приближении по формуле (6.7) в зависимости от Re I .

8.Определяется QII =ƒ( λII ) во втором приближении по формуле пунк-

та 2.

9. Находится относительная погрешность δ = (Qп −QI )/ QII 100% . Если δ ≤ δдоп , то решение заканчивается (для учебных задач δдоп =5%). В про-

тивном случае выполняется решение в третьем приближении. Обычно бывает достаточно двух или трех приближений для получения приемлемой точности.

Задача III. Дано: размеры трубопроводов (кроме диаметра d), шероховатость его стенок , свойства жидкости (ρ, ν), напор H, расход Q.

Определить диаметр трубопровода.

Решение.

При решении этой задачи возникают затруднения с непосредственным определением значения λ, аналогичные задаче второго типа. Поэтому решение целесообразно выполнять графоаналитическим методом.

vk.com/club152685050 | vk.com/id446425943

1.Задается несколько значений диаметров d1,d2,..., dn .

2.Для каждого значения di определяется соответствующее значение на-

пора H при заданном расходе Q ( п раз разрешается задача первого типа).

3.По результатам расчета строится график H = ƒ(d).

4.По графику определяется искомый диаметр d, соответствующий заданному значению напора H.

Методика решения задач первого и второго типа для простого трубопровода, состоящего из п последовательных участков различного диаметра, не отличается от изложенной выше. При этом для упрощения расчетных формул следует выражать скорости vi на каждом участке трубопровода через скорость

vn на последнем участке или через расход Q. Используя уравнение расхода (6.2), получим

	Sn			2	Q		4Q
		dn
vi = vn		= vn		или vi =		=		.
	Si				Si		πdi 2
			di

Необходимо также иметь в виду, что число Рейнольдса Rei , а следовательно, и коэффициент λi на каждом участке такого трубопровода имеет свое значение.

6.2. Примеры решения задач

Задача 6.2.1. Определить избыточное давление над поверхностью керосина (плотность ρ=808 кг/м3 , кинематический коэффициент вязкости

ν = 0,025 Ст) при его истечении из закрытого резервуара в атмосферу по трубопроводу длиной l = 5,0 м и диаметром d = 35 мм, если расход Q = 2,5 л/с. Коэффициент сопротивления вентиля ξвент = 4,0 . Шероховатость стенок трубы

= 0,05 мм. Уровень жидкости в резервуаре считать постоянным и равным

H 0 = 2,0 м (рис.6.1).

Дано: l = 5,0 м;

H 0 = 2,0 м;

ρ = 808 кг/м3 ;

вент

= 4,0;

= 0,05 мм = 0,05 10−3 м;

d = 35 мм = 35 10−3 м;

ν = 0,025 Ст = 2,5 10−6 м2

/ с;

Q = 2,5 л/с = 2,5 10−3 м3 / с.

Определить: ри.

Рис. 6.1.

Решение. 1. Составим уравнение Бернулли для сечений 1-1 и 2-2 относи-

тельно плоскости сравнения 0-0:

+ ∑h1−2 .

z1 +

+ α1

= z2 +

+ α2

ρg

vk.com/club152685050 | vk.com/id446425943

Имеем:

● для сечения 1-1-

● для сечения 2-2 -

= H o ;

ризб = ри ;

v1 = 0;

z2 = 0;

pизб

= 0 ;

v2 = v .

Потери напора

= hдл + ∑hм = (λl / d +ζвх +ζвент ) v 2 / 2g ,

∑h1−2

где ζвх =0,5 -

коэффициент сопротивления “вход в трубу”; λ -

коэффициент

гидравлического трения.

Перепишем уравнение Бернулли, выразив входящие в него величины,

H o +

ри

v 2

( 6.13)

α2

+λ

+ξвх

+ξ

вент

ρg

2. Из (6.13) получим расчетную формулу для искомой величины ри :

ри

α2

+λ

+ξвх +ξвент

− H о ρg .

Выразив среднюю скорость через расход - v = Q

, будем иметь

πd2

8Q 2

ри =

α2 +λ

+ζ

вх

+ζвент

− H

о ρg .

(6.14)

3. Определяем число Рейнольдса

Re =

4 2,5 10−3

= 36,4 103 .

πdν

3,14 35 10−3 2,5 10−3

Так как Re > Reкр=2300, то режим - турбулентный.

4. Находим коэффициент гидравлического трения λ по универсальной формуле Альтшуля для турбулентного режима:

		68 0,25		005,		68	0,25
λ = 011,	+		= 011,		+		= 00264,.
				35
d		Re				364, 103

Коэффициент кинетической энергии при турбулентном режиме α2 = 1,0 .

5. Вычислим искомую величину ри

по формуле (6.14):

5,0

8 (2,5 10−3 )2

ри = 1,0

+0,0264

+ 0,5

+ 4,0

−2,0 808 9,81 =

−3

−3 4

35 10

3,14

(35 10 ) 9,81

=9,51 103 Па.

Задача 6.2.2. Определить

расход

при

истечении керосина (плотность

ρ=808 кг/м3 ; кинематический коэффициент вязкости ν=0,025 Ст) из закрытого резервуара с избыточным давлением ри = 10,5 кПа в атмосферу по трубопрово-

ду длиной l=5,0м и диаметром d=35мм. Коэффициент сопротивления вентиля ζвент = 4,0 . Шероховатость стенок трубы = 0,05мм. Уровень жидкости в ре-

зервуаре считать постоянным и равным H 0 = 2,0 м (см. рис. 6.1).

vk.com/club152685050 | vk.com/id446425943

Дано: l= 5,0 м;	H 0 = 2,0 м;	d=35 мм = 35 10−3 м;
ρ = 808 кг/м3 ;	ξвент = 4,0 ;	pи =10,5 кПа =10,5 103	Па
=0,05мм = 10−3 м;		ν = 0,025 Ст = 2,5 10−6	м2/с;
Определить Q.

Решение. 1. Составление уравнения Бернулли приведено в пункте 1 решения задачи 6.2.1.

2. Получим расчетную формулу для искомой величины Q. Из уравнения

(6.13) имеем v =

2g(H о + ри / ρg )

α2 +λ

+ξвх +ξвент

2g(H о + ри / ρg )

Расход будет равен Q = νS =

πd 2

+λ l

+ζ

вх

+ζ

вент

Задачу решаем методом последовательных приближений.

3. Так как керосин - маловязкая жидкость, то предположим, что режим течения - турбулентный. Полагая в первом приближении, что течение в зоне квадратичного сопротивления, имеем:

-коэффициент кинетической энергии α2 =1;

-коэффициент гидравлического трения λI = 0,11(0,05 / 35)0,25 = 0,0214 . Находим расход в первом приближении:

3,14 (35 10−3 )2

2 9,81(2,0 +10,5 103 /808

9,81)

= 2,65

−3

/ с.

1 + 0,0214

5,0

+ 0,5 + 4,0

35 10−3

Число Рейнольдса в первом приближении равно

ReI =

4 2,65 10−3

38,6 103 .

πdν

3,14 35 10−3 2,5 10−6

Так как ReI> Reкр=2300, то режим - турбулентный.

4. Уточняем значение коэффициента λ во втором приближении:

0,25

005,

0,25

λII

= 011,

= 00261,.

38,6 103

Расход во втором приближении равен

(35 10−3 )

10,5 103

314,

2 9,81

2,0 +

QII

808

9,81

= 2,56 10−3 м3 / с.

5,0

+ 0,0261

+ 0,5 + 4,0

35 10−3

vk.com/club152685050 \| vk.com/id446425943
Относительная погрешность
δ =	(QII	−QI )	100 =	(2,56 10−3 − 2,65 10	−3 )	100	= 3,5% .
	QI			2,56 10−3

Полученная		погрешность		δ < δдол=5%, поэтому за			искомый расход

принимаем Q=2,56·10-3 м3/с=2,56 л/с.

Задача 6.2.3. Керосин (плотность ρ=808 кг/м3 ; кинематический коэффициент вязкости ν=0,025 Ст) вытекает из закрытого резервуара с избыточным давлением ри =10,5 кПа в атмосферу по трубопроводу длиной l=5,0м. Шерохо-

ватость стенок трубы =0,05 мм. Коэффициент сопротивления вентиля ζвент = 4,0 . Уровень жидкости в резервуаре считать постоянным и равным

Но=2,0 м.

Определить диаметр трубопровода, необходимый для обеспечения расхо-

да Q=2,5 л/с. (см. рис. 6.1).			pи =10,5 кПа = 10,5 103 Па;
Дано:	l=5,0 м;	ζвент = 4,0 ;	pи =10,5 кПа = 10,5 103 Па;
	H=2,0 м;	ρ=808кг/м3 ;	Q=2,5л/с=2,5 10−3 м3 /с.
	=0,05 мм;	ν = 0,025 Ст = 2,5 10−6 м2 /с;

Определить: d.

Решение. 1. Задаемся рядом значений диаметров d i = 30; 40; 50 мм

2. Для каждого значения диаметра решаем задачу первого типа: определяем величину напора, потребляемого для получения заданного расхода. (Составление уравнения Бернулли приведено в пункте 1 решения задачи 6.2.1).

Обозначим H o + ри		ρg = H		и выразим	скорость через		расход
v=Q S = 4Q πd2 .
Тогда получим расчетную формулу для напора:
			l		8Q 2
H =	α2 +λ			+ζвх +ζвент		.	(6.15)
			d
				π2 d 4 g

3. Вычисляем число Рейнольдса, соответствующее каждому диаметру:

Rei =

4 2,5 10−3

1,27

103;

πdi ν

3,14 di

2,5 10−6

Re =

1,27

103 =

42,3 103 ;

1,27

103 = 31,8 103;

10−3

40 10−3

1.,27

Re3

103 = 25,4 103.

50 10−3

Во всех случаях режим движения турбулентный.

Коэффициент кинетической энергии при турбулентном режиме α2 =1,0.

4. Определяем коэффициент гидравлического трения по универсальной формуле Альтшуля для турбулентного режима

vk.com/club152685050 | vk.com/id446425943

			68	0,25
		+			:

	λi = 0,11
	di		Rei
λ1	= 0,11(0,05 / 30 +68 / 42,3 103 )0,25					= 0,0263;
λ2	= 0,11(0,05 / 40 +68 / 31,8 103 )0,25					= 0,0265;
λ3	= 0,11(0,05 / 50 +68 / 25,4 103 )0,25					= 0,0271.

5. Определяем значения напора по формуле (6.15):

5,0

8 (2,5 10−3 )2

= 1 + 0,0263

+ 0,5

+ 4,0

= 6,31м;

10−3

2 (30 10−3 )4 9,81

3,14

5,0

8 (2,5 10−3 )2

= 1

+ 0,0265

+ 0,5 +

4,0

=1,78 м;

40 10−3

3,142 (40 10−3 )4 9,81

5,0

8 (2,5 10−3 )2

= 1

+ 0,0271

+ 0,5

4,0

= 0,68 м.

10−3

3,142 (50 10−3 )4 9,81

6. Строим график H=ƒ(d) (рис. 6.2).

Вычисляем заданный напор:

10,5 103

зад

= H о +

ри

2,0 +

= 3,32м .

ρg

808 9,81

По графику находим искомый диаметр, соответствующий заданному напору, d иск= 35мм.

Рис. 6.2

vk.com/club152685050 | vk.com/id446425943

6.3. Задачи

6-1÷2. Из резервуара по трубопроводу ( d1, l1 и d2 , l2 ) подается вода на

высоту H 2 =12,0 м. Шероховатость стенок трубопровода	= 0,15 мм. Коэффи-
циент сопротивления для поворотов принять равным ζпов	= 0,30, а для крана -
ζк.

Какое давление необходимо поддерживать в резервуаре, если уровень воды в нем принять постоянным, равным H1 , а расход воды через кран равен

Q=1,2 л/с?

6-3÷4. Из резервуара по трубопроводу ( d1, l1 и d2 , l2 ) подается вода на высоту H 2 =10,0 м. Шероховатость стенок трубопровода = 0,20 мм. Коэффициент сопротивления для крана принять равным ζк, а для поворотов трубопро-

вода - ζпов = 0,40 .

Определить расход воды через кран, если уровень H1 воды в резервуаре постоянный, а показание манометра составляет pм .

6-5÷6. По трубопроводу длиной l1 насосом подается топливо (ρ = 900 кг/м3 ) на высоту H1 . Избыточное давление, создаваемое насосом в на-

чале трубопровода, равно рм. Трубопровод считать гидравлически гладким. Местные потери в трубопроводе принять равными 10% потерь на трение по длине.

Определить диаметр трубопровода, обеспечивающий расход топлива

Q=10,0 л/с.

6-7÷8. По напорному трубопроводу диаметром d1 и длиной l1 необходимо подавать насосом воду c расходом Q= 12,5 л/с. Высота подъема воды H1 .

Определить увеличение давления нагнетания рмнасоса при возрастаю-

щих значениях шероховатости стенок в процессе эксплуатации труб от

0,20мм до 1,2 мм.

К задачам 6-1÷4

К задачам 6-5÷8

vk.com/club152685050 | vk.com/id446425943

6-9÷10. По вертикальной трубе ( d1, l1 и d2 , l2 ), соединяющей закрытый и

открытый резервуары, перетекает керосин (ρ=835 кг/м3 ). Верхний резервуар заполнен до уровня H1 , показание манометра составляет рм. Коэффициент сопротивления крана ζк.

Определить расход керосина, считая шероховатость труб равной =0,2мм, а уровни керосина в резервуарах постоянными.

6-11÷12. Из закрытого резервуара, заполненного до уровня H1 , по вертикальной трубе ( d1, l1 и d2 , l2 ) перетекает бензин (ρ=765 кг/м3 ) в нижний от-

крытый резервуар с расходом Q=1,2 л/с. Шероховатость стенок трубопровода =0,10 мм, коэффициент сопротивления крана ζк.

Определить показание манометра в верхнем резервуаре, считая уровни бензина в резервуарах постоянными рм.

	6-13÷14.	Из	открытого	резервуара		через	вертикальную	трубу
( d1, l1	и d2 , l2 ) в атмосферу вытекает вода. Уровень в резервуаре постоянный,
глубина H1 . Шероховатость стенок труб					=0,35 мм. Коэффициент сопротив-
ления крана ζк .
	Определить расход воды.
	6-15÷16.	Из	открытого	резервуара		через	вертикальную	трубу
( d1, l1	и d2 , l2 )	в	атмосферу вытекает		вода.	Шероховатость стенок		труб

=0,50мм. Коэффициент сопротивления крана ζк.

Считая уровень H1 воды в резервуаре постоянным, определить его значение, если расход Q=4,0 л/с.

К задачам 6-9÷12

К задачам 6-13÷16

vk.com/club152685050 | vk.com/id446425943

6-17÷18. Насос по трубопроводу диаметром d1 и длиной l1перекачивает

топливо (ρ=900 кг/м3 ) в резервуар на высоту H1 . Шероховатость стенок трубопровода = 0,15 мм, коэффициент сопротивления колен ζ кол = 0,40 , а вентиля ζв .

Определить давление pм , которое должен создавать насос, чтобы подать топливо с расходом Q=25 л/с.

6-19÷20. По трубопроводу длиной l1 насос перекачивает топливо

(ρ=880кг/м3 ) в резервуар на высоту H1 . Манометрическое давление, создаваемое насосом, равно рм. Шероховатость стенок трубопровода =0,25 мм. Мест-

ные потери в трубопроводе принять равными 15% потерь на трение по длине. Определить диаметр трубопровода, обеспечивающий расход топлива

Q=5,0 л/с.

6-21÷22. Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу ( d1 ,l1 и d2 ,l2 ). Горизонтальный участок заглублен под уро-

вень на H1 , наклонный участок имеет высоту H 2 =15,0 м. Шероховатость сте-

нок трубопровода = 0,20 мм, потерю напора на повороте не учитывать. Определить, каков должен быть коэффициент сопротивления задвижки ζ

при расходе в трубопроводе Q=17 л/с?

6-23÷24. Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу ( d1, l1 и d2 , l2 ). Горизонтальный участок заглублен под уро-

вень на H1 , наклонный участок имеет высотуH 2 =18,0 м. Шероховатость стенок трубопровода =0,50 мм, коэффициент сопротивления вентиля ζв , пово-

рота - ζпов = 0,25 .

Определить расход воды.

К задачам 6-17÷20

К задачам 6-21÷24

vk.com/club152685050 | vk.com/id446425943

6-25÷26. Насос забирает масло (ρ= 920 кг/м3 ) из открытого бака по всасывающему трубопроводу диаметром d1 и длиной l1 . Уровень масла в баке ниже оси насоса на H1 . Вакуумметр, установленный перед насосом, показывает

рвак =30 кПа.

Определить расход масла, принимая местные потери напора в трубопроводе равными 10% от потерь на трение по длине.

6-27÷28. Насос забирает масло (ρ=890 кг/м3 ) из открытого бака по всасывающему трубопроводу диаметром d1 и длиной l1 . Уровень масла в баке ниже оси насоса на H1 . Трубопровод считать гидравлически гладким, коэффициент сопротивления приемника ζпр =4,0, колена - ζкол = 0,5 .

Определить показание вакуумметра перед насосом, если насос обеспечивает расход Q=12,0 л/с.

6-29÷30. Из открытого резервуара по трубопроводу ( d1, l1 и d2 , l2 ) про-

исходит истечение воды в атмосферу при постоянном напоре H=4,0 м. Коэффициент сопротивления крана ζк, шероховатость стенок трубы =0,50 мм.

Определить расход воды, если выходное отверстие трубопровода расположено выше входного на величину H1 .

6-31÷32. Из открытого резервуара по трубопроводу ( d1, l1 и d2 , l2 ) про-

исходит истечение воды в атмосферу. Выходное отверстие расположено выше входного на величину H1 . Шероховатость стенок трубопровода =0,50 мм, ко-

эффициент сопротивления крана ζк.

Определить, при каком напоре Н можно получить расход Q=5,6 л/с?

К задачам 6-25÷28 К задачам 6-29÷32

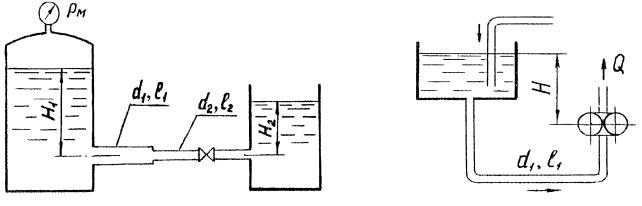
vk.com/club152685050 | vk.com/id446425943

6-33÷34. Горизонтальная труба ( d1, l1 и d2 , l2 ) соединяет закрытый, где поддерживается избыточное давление рм , и открытый резервуары с постоянными уровнями H1 и H 2 ( H 2 =1,20 м).

Определить расход воды, если коэффициент сопротивления вентиля ζв , а шероховатость стенок трубы =0,50 мм.

6-35÷36. Закрытый и открытый резервуары с постоянными уровнями H1 и H 2 ( H 2 =0,80 м) соединены горизонтальной трубой ( d1, l1 и d2 , l2 ), имеющей

шероховатость стенок	=0,50 мм.
Какое давление	рм необходимо поддерживать в закрытом резервуаре,

чтобы расход воды по трубе составлял Q=10 л/с, если коэффициент сопротивления вентиля ζв ?

6-37÷38. Определить давление на входе в шестеренный насос системы смазки, подающий расход Q=1,0 л/с масла (ρ=890 кг/м3 ). Размеры всасывающего трубопровода d1 и l1, шероховатость его стенок =0,10 мм. Входное се-

чение насоса расположено ниже свободной поверхности в масляном баке на H1 . Местные потери в трубопроводе принимать равными 10% потерь на трение

по длине.

Как изменится давление перед насосом, если в результате нагрева вязкость масла уменьшится в 20 раз ?

6-39÷40. На входе в шестеренный насос системы смазки обеспечивается вакуум рвак =30 кПа. Входное сечение насоса расположено ниже свободной по-

верхности в масляном баке на H1 . Размеры всасывающего трубопровода d1 и l1. Трубопровод считать гидравлически гладким. Местные потери в трубопроводе принимать равными 10% потерь на трение по длине.

Определить расход Q масла (ρ=900 кг/м3 ) в трубопроводе.

К задачам 6-33÷36

К задачам 6-37÷40

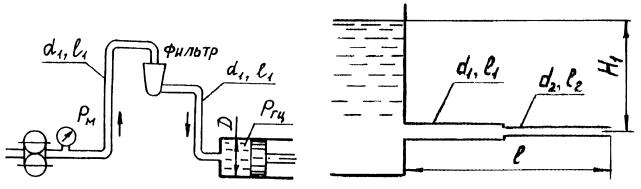
vk.com/club152685050 | vk.com/id446425943

6-41÷42. Насос подает масло (ρ=900 кг/м3 ) в гидроцилиндр диаметром D=150 мм по трубопроводу длиной l1. Давление нагнетания насоса равно рм . Избыточное давление в гидроцилиндре рг =1,5 МПа. Трубопровод считать гид-

равлически гладким. Местные потери принять равными 20% потерь на трение по длине.

Определить, каким должен быть диаметр трубопровода, чтобы обеспечить скорость движения поршня vп = 0,1 м/с?

6-43÷44. Насос по трубопроводу размерами d1 и l1 через фильтр ( ζф =9,0)

подает масло в гидроцилиндр. Давление нагнетания насоса рм . Коэффициент
сопротивления колен ζкол = 0,40 .Трубы гидравлически гладкие.	Скоростью
движения поршня гидроцилиндра можно пренебречь.
Определить, как изменится давление в гидроцилиндре при изменении
температуры масла от 5°С ( ν=3,0 Ст; ρ=890 кг/м3 ) до 50°С	(ν=0,2 Ст,
ρ=850кг/м3 ), если расход масла по трубопроводу Q=1,7 л/с?
6-45÷46. Для подачи воды в количестве Q=0,025 м3 /с на	расстояние

l=500м под напором H1	можно	использовать трубы диаметром d1 и d2, шеро-
ховатость стенок которых	=1,0	мм.

Определить необходимые длины участков l1 и l2.

6-47÷48. По трубопроводу размерами d1, l1 и d2 , l2 подается вода под постоянным напором H1 .

Определить расход воды, если шероховатость стенок трубопровода

=0,50 мм.
К задачам 6-41÷44	К задачам 6-45÷48

vk.com/club152685050 | vk.com/id446425943

6-49÷50. По горизонтальному трубопроводу длиной l1необходимо пере-

качивать нефть (ρ=910 кг/м3 ) с расходом 60 л/с при условии, чтобы падение давления в трубопроводе не превышало р= 4,0 МПа. Шероховатость стенок

трубопровода	=0,20 мм.
Определить диаметр трубопровода.
6-51÷52.	По трубопроводу размерами d1, l1 и d2 , l2 подается бензин

(ρ=765кг/м3 ) из бака с избыточным давлением рм в расположенный выше бак, где поддерживается вакуум рвак =20кПа. Шероховатость стенок трубопровода

= 0,10 мм. Коэффициент сопротивления вентиля ζв .

Определить расход бензина, считая разность уровней в баках постоянной, равной H1 .

6-53÷54. По трубопроводу ( d1, l1 и d2 , l2 ) подается керосин (ρ=835кг/м3 )

из бака с избыточным давлением рм в расположенный выше бак, где поддерживается вакуум рвак =10 кПа. Трубопровод считать гидравлически гладким. Ко-

эффициент сопротивления вентиля ζв .

Определить, при какой разности уровней H1 керосина в баках можно получить расход Q=1,2 л/с?

6-55÷56. Из бака с избыточным давлением рм необходимо подать по тру-

бопроводу с постоянным диаметром масло (ρ=910 кг/м3 ) в бак, где поддерживается вакуум рвак =30 кПа.

Определить максимальную длину трубопровода, чтобы при разности уровней H1 в баках по трубопроводу проходило 0,20 л/с масла. Местные поте-

ри напора в трубопроводе принять равными 10% от потерь по его длине.

К задачам 6-51÷56

1 / 321 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
19.08.20195.21 Mб1289АЗЕРБАЙДЖАН нефть.pdf
#
19.08.201911.07 Mб173Американское бурение.pdf
#
20.08.2019516.03 Кб12АРГУМЕНТЫ ЗА РАСШИРЕНИЕ ЭКСПОРТА НЕФТИ И ГАЗА.pdf
#
14.08.201914.1 Mб21Арктика нефть.pdf
#
15.09.2019227.18 Кб17аттестации Крепление скважин.pdf
#
31.08.201925.4 Mб77аэродинамики и гидромеханики.pdf
#
06.09.2019409.2 Кб30БУРЕНИЕ ЛИДЕРНЫХ СКВАЖИН.pdf
#
10.08.2019420.02 Кб28БУРЕНИЕ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН.pdf
#
20.08.201918.78 Mб18БУРОВЫЕ ПРОМЫВОЧНЫЕ И ТАМПОНАЖНЫЕ РАСТВОРЫ.pdf
#
15.09.2019407.93 Кб11Вопросы к экзамену Технологии транспортировки и хранения нефти.pdf
#
21.08.2019851.27 Кб19ВЫПУСКНОЙ нефть и газ.pdf