3.3.4. Загальна модель управління запасами в одному періоді

Модель може бути сформульована так. Товари можна замовляти тільки на початку періоду. Одиниця товару коштує грн. незалежно від обсягу замовленої партії. Товар продається по ціні грн. за одиницю. Нехай f(x) – щільність імовірності попиту на продукцію протягом періоду. Якщо в момент виникнення вимоги на складі немає товарів, то окрім недоодержаного прибутку, фірма несе збитки, пов’язані із втратою клієнтів, які можна оцінити у грн. за одиницю товару. Усі нерозпродані до кінця періоду товари можуть бути реалізовані по ціні грн. ( . Треба визначити оптимальний обсяг наявних запасів у початковий момент часу за критерієм максимуму середнього прибутку за період.

Розглянемо окремо дискретну і неперервну моделі.

Дискретна модель

Введемо позначення:

– імовірність попиту k одиниць продукції протягом періоду;

–обсяг замовленої у періоді продукції;

– вартість продажу одиниці товару;

– вартість продажу продукції, яка не була реалізована до кінця періоду;

– вартість одиниці закуповуваної продукції;

– збитки, пов’язані із незадоволенням попиту.

Нехай попит є дискретна випадкова величина з розподілом Якщо на початку періоду було заготовлено запас у q одиниць продукції, то математичне сподівання прибутку за період складе

(3.37)

де – середній попит продукції за період.

Значення q, яке максимізує середній прибуток, є таке найбільше q, для якого .

Оскільки

(3.38)

де то оптимальним , буде найбільше q, для якого

(3.39)

Наведемо приклади, які ілюструють усю різноманітність практичних задач, у яких використовується наведена модель.

Приклад 3.11. У великому продовольчому магазині необхідно визначити, скільки хліба потрібно замовляти на день. Вивчення продажу хліба показало, що попит за день можна вважати випадковою величиною, розподіленою за нормальним законом із середнім 300 і середнім квадратичним відхиленням 50. Один батон продається за 1,2 грош. од. Собівартість товару для магазину складає 0,9 грош. од. за батон. Весь не проданий хліб збувається на наступний день по ціні 0,72 грош. од. за штуку. Треба визначити оптимальний розмір закупівлі хліба, який максимізує середню виручку.

У прийнятих у моделі позначеннях маємо:

Алгоритм реалізації моделі

 задаємо висхідні дані

 обчислюємо імовірність р (критичне відношення );

 для нормованої випадкової величини з параметрами визначаємо квантиль нормованого нормального розподілу, де – функція, обернена до функції . У Mathcad величина визначається за оператором . Оптимальна кількість товару яка потрібна для задоволення попиту на даний період, визначається за формулою

Для визначення можна застосувати і інший алгоритм, розв’язуючи рівняння відносно , де . Розв’язуючи це рівняння за допомогою оператора Mathcad знаходимо значення яке співпадає з попереднім значенням.

 записуємо вираз для математичного сподівання прибутку P(q). Функції , які входять у цей вираз, можна обчислювати за операторами Mathcad

;

 визначаємо середню кількість невикористаних автомобілів n і максимальне значення функції прибутку

Алгоритм у Mathcad

Алгоритм 1

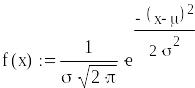
Алгоритм 2

Порівняємо середню денну виручку для випадку, коли у день закуповується батонів, із середньою виручкою, коли у день закуповується батонів, тобто таку кількість, яка дорівнює середньому попиту .

При одержуємо

_{Абсолютна і відносна зміна прибутку}

Коментар. Оптимальна політика управління запасами хліба полягає у закупівлі щоденно батонів по ціні 0,9 грош. од. При продажу батонів по ціні грош. од. у день і реалізації їх на наступний день по ціні 0,72 грош. од. при середній кількості непроданих батонів, математичне сподівання прибутку дорівнюватиме грош. од.

Якщо закуповувати не а , то математичне сподівання прибутку дорівнюватиме грош. од.

Таким чином, використовуючи оптимальне значення одержимо у порівнянні з щоденний виграш у 0,47 грош. од., тобто біля 0,6 % від усієї виручки. ▲

Приклад 3.12. В умовах попередньої задачі розглянемо тепер випадок, коли при неспроможності задовольнити попит покупців магазин несе збитки, пов’язані із втратою очікуваного прибутку. Ці збитки оцінюються у розмірі грош. од за одиницю товару.

Як і в попередній задачі визначимо оптимальний обсяг замовлення батонів і максимальний очікуваний прибуток , який може одержати магазин, замовляючи батони у кількості штук. Визначимо також величину виручки , якщо замовляти батонів.

Для розв’язання цієї задачі застосуємо попередній алгоритм.

Алгоритм у Mathcad

Коментар. Результати розрахунків показують, що виручка у першому випадку, коли замовляється батонів, дорівнює грош. од. і помітно відрізняється від виручки грош. од., одержуваної при середній їх кількості батонів. ▲

Приклад 3.13. Кондитерська замовляє шоколад у фірми кондитерських виробів, яка обслуговує декілька магазинів. Власник кондитерської повинен вирішити, скільки йому слід замовляти шоколадних фігурок до свята. Замовлення потрібне не пізніше, ніж за 2 місяці до свята. Кожна шоколадна фігурка обходиться магазину у 10 грош. од., а продається за 28 грош. од. Сума, витрачена на нереалізований за свята шоколад, складає платіжний дефіцит. Можна стверджувати, що за тиждень свят магазину напевно вдасться продати не менше 100 фігурок, але не більше 500. Продаж будь-якої кількості між 100 і 500 вважається рівноімовірними подіями, тобто магазин припускає, що обсяг попиту рівномірно розподілений на інтервалі від 100 до 500. Визначимо оптимальний обсяг замовлення шоколаду і прибуток, який може одержати кондитерська.

Якщо вважати обсяг попиту неперервною випадковою величиною, розподіленою за рівномірним законом, то відповідна щільність імовірностей дорівнює

Функція визначається співвідношенням

Із наведених вище даних і умова для визначення оптимального має вигляд

де

Середня кількість нерозпроданих до кінця свят шоколадних фігурок при умові, що до початку свят їх було замовлено q штук , дорівнює

Середній очікуваний прибуток як функція розміру замовлення визначається наступним співвідношенням

Алгоритм у Mathcad

_{Оптимальний обсяг поставки}

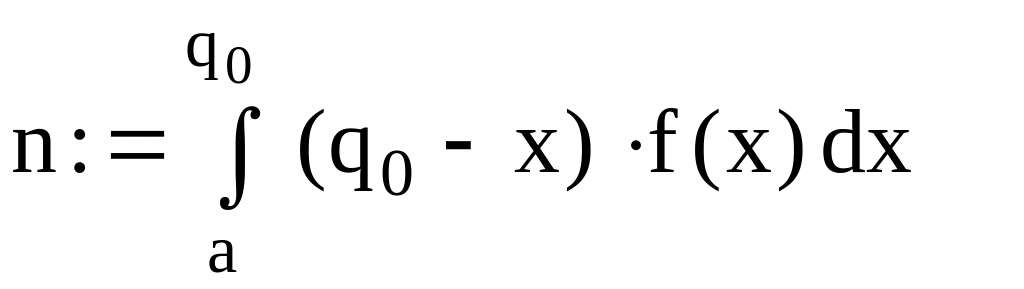або

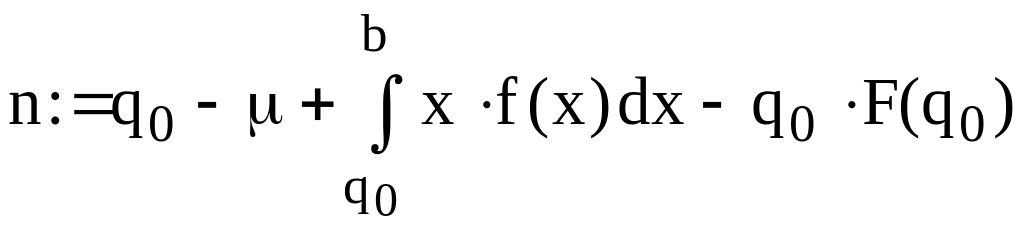
Коментар. Оскільки і , то середня кількість нерозпроданих за свята фігурок при умові, що до початку періоду їх було замовлено штук дорівнює штуки. Середній прибуток складає грош. од. і грош. од.

Результати розрахунків показують, що виручка у першому випадку, коли замовляється батонів дорівнює грош. од. і помітно відрізняється від виручки грош. од., одержуваної при замовленні батонів.

Таким чином, якщо розмір замовлення на 29 одиниць перевищує середній обсяг попиту, то це приводить до збільшення прибутку на 114,3 грош. од. Але слід звернути увагу на те, що середня кількість нереалізованих одиниць товару може складати одиниць. ▲

Приклад 3.14. Одночасно з випуском літаків виготовляються і деякі запасні частини до них. Після того, як збірка літака закінчена, вже важко дістати до нього додаткові запасні частини. Після закінчення збірки літака треба визначити, скільки запасних частин певного типу слід мати у комплекті до нього. Припускається, що попит на запасні частини цього типу невеликий і розподілений за законом Пуассона, а інтенсивність попиту (на основі накопиченого досвіду) складає одиниць у рік. Розподіл терміну експлуатації літака точно невідомий. Припускається, що він може бути описаний гама-розподілом із середнім років і середнім квадратичним відхиленням роки. Кожна запасна частина розглядуваного типу коштує 10000 грош. од., а якщо до моменту виходу із ладу всього літака які-небудь запасні частини залишаються не використаними, то кожна із них коштує всього лише 500 грош. од. Якщо усі запасні частини комплекту витрачені, то для того, щоб дістати ще один запасний блок, необхідно витратити 26000 грош. од.

Щоб визначити, скільки запасних частин повинно бути у комплекті до літака, необхідно спочатку знайти безумовний розподіл величини попиту за час експлуатації літака. Оскільки попит на запасні частини розподілений за законом Пуассона, а термін експлуатації літака має гама-розподіл, то безумовний розподіл величини попиту представляється від’ємним біноміальним розподілом зі щільністю імовірності

Для визначення використаємо співвідношення

,

які зв’язують із середнім значенням і середнім квадратичним відхиленням для гама-розподілу.

Функція від’ємного біноміального розподілу визначається співвідношенням

Із наведених даних видно, що і Максимізація прибутку при еквівалентна мінімізації середніх витрат. Отже, у цьому випадку застосовується формула аналогічна (3.18).

Таким чином, математичне сподівання функції витрат дорівнює

Якщо q означає кількість запасних частин у комплекті, то оптимальне значення яке мінімізує середні витрати G(q), дорівнює найбільшому q, для якого виконується умова

Цю умову можна представити у вигляді

Середній попит на запасні частини за час експлуатації літака (6 років) дорівнює одиниць. Якщо у комплекті до літака є q запасних частин, то середня кількість запасних частин, не використаних до моменту зняття літака з експлуатації, дорівнює

Для знайденого оптимального значення визначаємо середню кількість невикористаних запасних частин і мінімальне значення функції витрат

Алгоритм реалізації моделі

 задаємо вхідні дані задачі

 визначаємо параметри від’ємного біноміального розподілу і записуємо вирази для щільності і функції цього розподілу відповідно;

 визначаємо критичне відношення (значення ймовірності p), яке є умовою для знаходження оптимального значення

 визначаємо оптимальний обсяг партії поповнення запасу . При обчисленні сум з верхнім індексом рівним береться число , значення якого достатнє для забезпечення потрібної точності обчислень;

 визначаємо кількість невикористаних запасних частин

 визначаємо мінімальне значення функції витрат

_{Алгоритм у Mathcad}

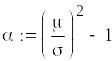
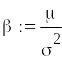
_{Мінімальне значення витрат}

Коментар. Стратегія управління запасами у даній системі полягає у створенні запасу у кількості комплектів деталей. При цьому середній залишок невикористаних деталей становитиме комплектів. При такій стратегії математичне сподівання мінімальних витрат буде дорівнювати тис. грош. од. ▲