3.2.2. Модель з рівномірним витрачанням запасів

Неперервна модель

У цьому випадку математичне сподівання втрат дорівнює

. (3.18)

За формулою диференціювання інтеграла по параметру, знаходимо

де .

Прирівнюючи знайдену похідну до нуля, встановлюємо, що мінімум G(s) досягається при такому значенні при якому

(3.19)

Покладемо Тоді умова (3.12) запишеться у вигляді

(3.20)

Дискретна модель

Припустимо, що попит на товар на інтервалі часу є випадковим і заданий рядом розподілу ймовірностей , де імовірність попиту на k одиниць товару. Витрати на зберігання одиниці товару в одиницю часу дорівнюють , нестача одиниці товару призводить до збитків у розмірі .

Розглянемо наступний приклад. Станція технічного обслуговування автомобілів має склад деталей. Деякі дорогокоштуючі деталі завжди повинні знаходитись на складі і видаватись за вимогою клієнтів, оскільки не можна допустити затримки у ремонті автомобілів. Який запас s цих деталей повинна мати станція технічного обслуговування на складі, щоб мати мінімум витрат, пов’язаних із зберіганням і незадоволеним попитом (втрата клієнта або термінова закупівля деталей за завищеними цінами тощо).

Позначимо через проміжок часу між послідовними моментами поповнення запасу. У випадку коли запас менше ніж попит , інтервал буде складатись із двох підінтервалів і , де – час, коли запас є, – коли запас відсутній. Припускаючи, що зміна запасу може відбуватись лінійно, будемо мати два випадки:

1. При середній запас на проміжку часу дорівнює

2. При середній запас на проміжку і середня нестача запасу на проміжку рівні

Математичне сподівання сумарних витрат дорівнює

(3.21)

Мінімум функції G(s) досягається у точці , для якої виконуються нерівності

(3.22)

де

,

Функція Р(s) за означенням дорівнює Як легко помітити, означає, що і відповідають оптимуму, а означає, що оптимуму відповідають і . Порівняння і L(s) зразу дає і

Приклад 3.5. Деталі, які зберігаються на складі, витрачаються рівномірно протягом дня. Витрати на зберігання однієї деталі на складі складають грн., а штраф за дефіцит деталі обходиться у грн. для спрощення обчислень покладемо Розподіл імовірностей попиту на деталі заданий у таблиці

Визначимо необхідний оптимальний щоденний запас деталей на складі s, щоб можливі витрати на зберігання запасу і збитки від дефіциту були б мінімальні.

Алгоритм реалізації моделі

 задаємо величини і розподіл імовірностей попиту

 визначаємо щільність збитків , функцію розподілу попиту Р(k) і його середнє значення m;

 записуємо вирази для цільової функції G(s) і функції L(s);

 визначаємо оптимальне значення обсягу запасу використовуючи співвідношення (3.10). Для цього використовується оператор Mathcad який дає значення , якщо задана умова виконується і 0 у протилежному випадку;

 визначаємо мінімальне значення цільової функції

Алгоритм у Mathcad

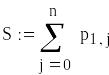
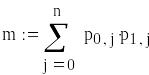
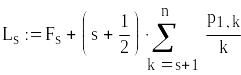
Визначення значення яке дає мінімум функції G(s)

Коментар. У даній моделі оптимальна політика управління запасами полягає у створенні щоденного запасу деталей на складі у кількості деталі при середньому значенні попиту деталі. Мінімальні втрати дорівнюють грн. ▲

Приклад 3.6. Розглянемо попередню модель при витратах , але попит розподілений за експоненціальним законом із щільністю розподілу ймовірностей де параметр розподілу, який дорівнює , m – середнє значення попиту. Для заданого розподілу ймовірностей середній попит m = 1,7, отже

Визначимо оптимальний рівень запасів і мінімальне значення математичного сподівання витрат

Обчислення проводимо за наступним алгоритмом:

 задаємо значення показників витрат і визначаємо величину ;

 задаємо параметр експоненціального розподілу і записуємо відповідні вирази для щільності розподілу ймовірностей і функції розподілу ;

 записуємо вирази для функцій і рівняння із якого визначаємо значення , яке є точкою мінімуму функції

Алгоритм у Mathcad

Розв’язання рівняння , визначення точки екстремуму і мінімуму функції

Коментар. Політика управління запасами у даній моделі полягає у створенні оптимального запасу у одиниць товару при середньому попиті одиниць. Мінімальні витрати дорівнюватимуть грн. ▲