3.2. Стохастичні моделі управління запасами з оптимальним рівнем запасів

3.2.1. Модель з миттєвим витрачанням запасів

Припустимо, що попит на продукцію, яка зберігається на складі на деякому

інтервалі часу T, є випадкова величина X і заданий її закон розподілу. Якщо Х дискретна випадкова величина, яка приймає значення = 0, 1, 2,…, то законом

розподілу її є ряд розподілу , де – імовірність попиту k. Якщо Х неперервна величина, то її закон розподілу задається щільністю розподілу ймовірностей f(x). Імовірності і щільність розподілу f(x) зазвичай оцінюються на основі експериментальних (статистичних) даних або теоретично.

Знаючи закон розподілу або , можна визначити математичне сподівання витрат, яке є економічною функцією для даної задачі. Задача управління запасами у даній моделі полягає у знаходженні такого рівня запасу , при якому математичне сподівання сумарних витрат приймає мінімальне значення.

Дискретна модель

Припустимо, що попит на інтервалі часу Т є випадковим і задано його закон розподілу

Позначимо через s – кількість одиниць товару, призначеного на склад. Можливі два взаємовиключні випадки:

1) – запас перевищує попит і надлишок товару продається із збитками, рівними на кожну одиницю товару;

2) – є нестача товару і термінове придбання одиниць товару викликає необхідність у позаплановому поповненні, що веде до збитків на одиницю товару.

Така ситуація виникає, наприклад, якщо одночасно із виготовленням устаткування виготовляються також запасні частини до нього. Якщо вироблено надлишок запасних частин, то надлишки доводиться розпродавати із деякими збитками; якщо ж їх кількість менша необхідної, то доводиться закуповувати недостатню кількість по більш високій ціні (типовий приклад – запасні частини для імпортної автомобільної техніки). Розглянуті випадки зображені на рис. 3.2.

Введемо позначення:

витрати на поповнення одиниці продукції

витрати на зберігання одиниці запасів;

витрати на одиницю дефіциту товару.

Y(t)

Y(t)

t

Знаючи розподіл імовірностей попиту можна визначити математичне

сподівання сумарних витрат, яке має вигляд

(3.10)

Отже, задача управління запасами у даній моделі полягає у знаходженні такого рівня запасу s, при якому математичне сподівання сумарних витрат набуде мінімального значення.

Мінімум функції має місце при значенні , яке задовольняє нерівностям

, (3.11)

де

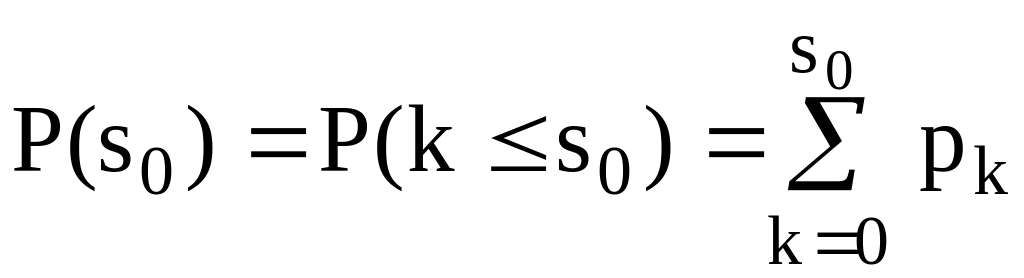(3.12)

– імовірність того, що рівень запасу не перевищує величини а

– щільність збитків.

Покажемо, як можна знайти мінімум функції , заданої формулою (3.10). Послідовно запишемо

Оскільки

.

Таким чином,

де імовірність того, що попит менше або дорівнює

Тим же способом можна показати, що

Припустимо тепер, що задовольняє нерівності

тобто запас, при якому витрати мінімальні. Тоді співвідношення для і запишеться у вигляді

або ,

а співвідношення для і у вигляді

або

Звідкіля

Позначаючи одержимо потрібне нам співвідношення (3.11).

Якщо виконуються нерівності (3.11), то звідси випливає, що

Зауважимо, що якщо для деякого виконується співвідношення

то (3.13)

тобто оптимум відповідає і

Аналогічно, якщо

то (3.14)

тобто оптимум відповідає і

Неперервна модель

У випадку, коли X – неперервна випадкова величина із щільністю розподілу ймовірностей , функція витрат має вигляд

. (3.15)

Щоб знайти мінімум функції , обчислимо її похідну, скориставшись формулою похідної від інтеграла по параметру. Одержуємо

де – функція зрізаного розподілу попиту.

Прирівнюючи похідну до нуля, отримаємо рівняння, якому задовольняє

(3.16)

Для зручного обчислення функції G(s), вираз (3.15) можна представити у вигляді

(3.17)

де – математичне сподівання розподілу попиту, а

, .

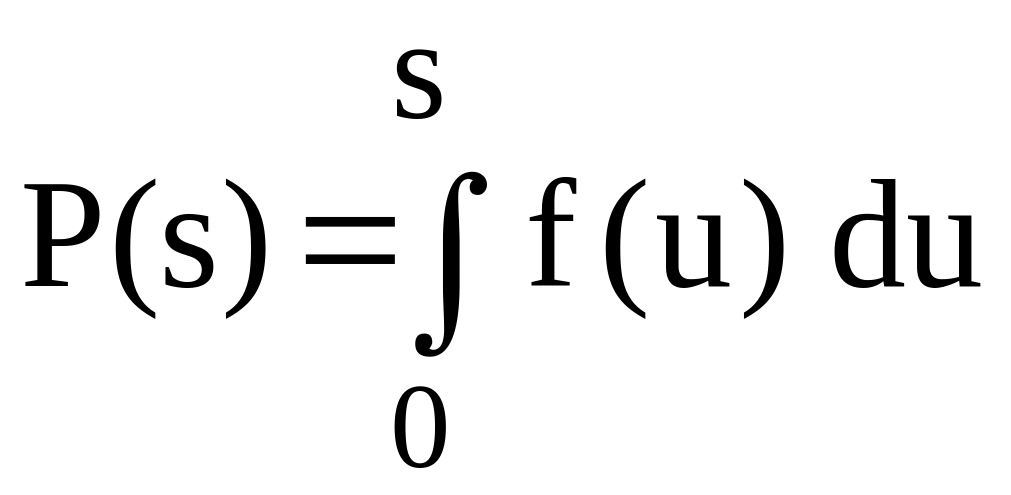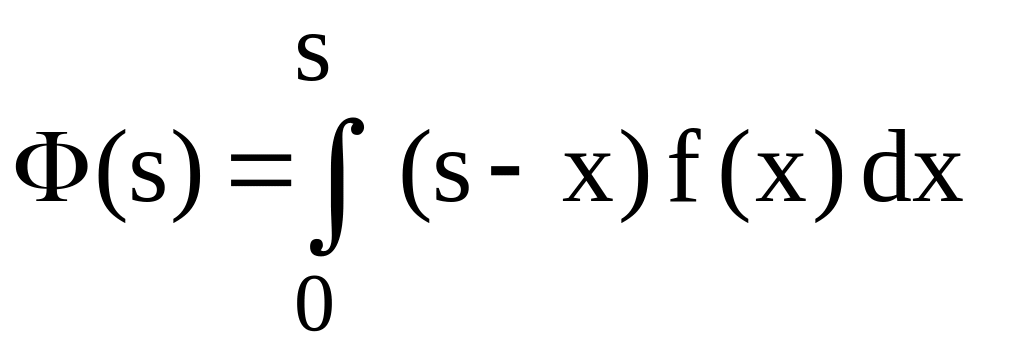Легко перевірити, що величина яка відповідає (3.16), дає мінімум економічної функції Дійсно, знайдемо другу похідну від функції і визначимо її знак

Оскільки не дорівнює нулю і то Це означає, що функція має мінімум при

Співвідношення (3.16), яке визначає мінімум функції у неперервному випадку, відповідає нерівностям (3.11), які відносяться до випадку, коли набуває цілочислові значення.

Зокрема, для нормального розподілу попиту з параметрами із (3.16) маємо

де функція нормального розподілу.

Таким чином, для визначення одержуємо вираз

У Mathcad значення визначається як квантиль нормального розподілу порядку

У випадку експоненціального розподілу попиту

.

Приклад 3.2.. Автотранспортна фірма здійснює обслуговування клієнтів, маючи власних автомобілів. Попит на транспортні послуги, виражений у кількості автомобілів, є дискретна випадкова величина X, задана рядом розподілу . Якщо у деякий день попит на автомобілі k нижче кількості наявних автомобілів s, то автомобілі, які безпосередньо не зайняті обслуговуванням клієнтів за замовленнями, використовуються на інших роботах, при цьому фірма втрачає прибуток у грош. од на один автомобіль. Якщо попит k вище кількості наявних автомобілів s, то для виконання своїх зобов’язань по обслуговуванню клієнтів у фірми виникає необхідність у оренді додаткових автомобілів, що веде до збитків у розмірі грош. од на один автомобіль.

Треба визначити:

 оптимальну кількість автомобілів , яку повинна мати фірма щоденно, щоб можливі втрати прибутку були мінімальні;

 втрати від нестачі автомобілів (штрафи від незадовільненого попиту плюс втрата можливого прибутку);

 залежність загальних витрат від втрат у наслідок дефіциту;

залежність математичного сподівання втрат від величини збитків у наслідок дефіциту автомобілів.

Алгоритм реалізації моделі

 задаємо величини , розподіл імовірностей попиту і визначаємо щільність збитків , середнє значення m і функцію розподілу попиту F(k);

 записуємо вираз для цільової функції ;

 визначаємо оптимальне значення обсягу запасу використовуючи співвідношення (3.11);

 визначаємо мінімальне значення цільової функції ;

 аналізуємо залежність цільової функції G(s) від втрат у наслідок дефіциту і будуємо графік залежності функції збитків від ;

 використовуючи умову (3.16), визначаємо діапазон збитків від незадовільненого попиту при умові, що оптимальний запас дорівнює ;

Алгоритм у Mathcad