§9. Непрерывные случайные величины

Непрерывной называется такая случайная величина, значения которой сплошь заполняют некоторый промежуток.

Непрерывная случайная величина обычно задаётся плотностью распределения f(x).

Свойства плотности распределения:

1) f(x)  0; 2) .

Функция распределения F(x) и плотность распределения f(x) связаны между собой равенствами: , .

Вероятность попадания непрерывной случайной величины на числовой промежуток [a; b] выражается через плотность распределения следующим образом: .

Математическое ожидание M[X] непрерывной случайной величины X определяется формулой .

Дисперсия D[X] непрерывной случайной величины X вычисляют по формулам

.

Среднее квадратическое отклонение [X] непрерывной случайной величины Х определяется так же, как и для дискретной случайной величины: .

9.1. Непрерывная случайная величина Х подчинена закону распределения с плотностью Найти числовые характеристики M[X], D[X], [X] данной случайной величины и P{0 < X < 1,5}.

9.2. Непрерывная случайная величина Х подчинена закону распределения с плотностью Найти коэффициент a, функцию распределения F(x) и P{X  0}, P{X = –1}, P{X > 0,5}.

9.3. Непрерывная случайная величина X имеет функцию распределения 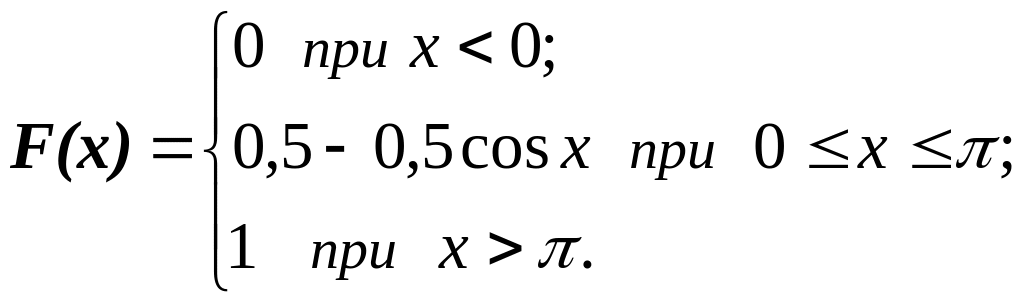Найти плотность распределения f(x) и . Построить графики функций f(x) и F(x).

9.4. Функция распределения непрерывной случайной величины Х имеет вид F(x) = a + b arctgx. Найти постоянные а и b, плотность распределения f(x) и P{0  X  1}.

9.5. Непрерывная случайная величина Х подчинена закону распределения с плотностью 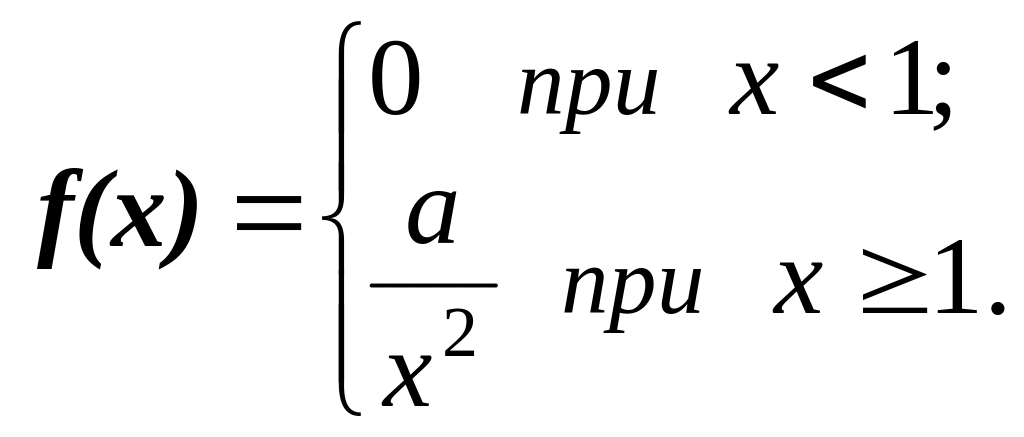Найти коэффициент а, функцию распределения F(x) и P{2 < X < 3}.

9.6. Непрерывная случайная величина X подчинена закону распределения с плотностью Найти , .

9.7. Непрерывная случайная величина Х имеет функцию распределения 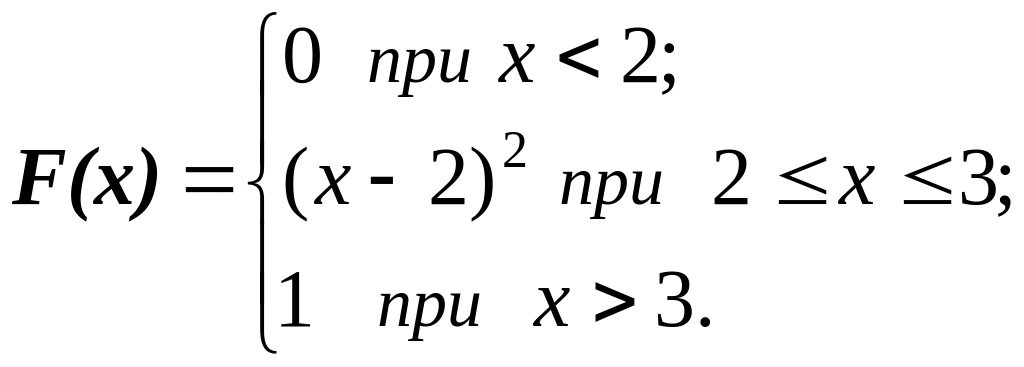. Найти плотность распределения f(x) и числовые характеристики M[X], D[X], [X] данной случайной величины.

9.8. Непрерывная случайная величина Х подчинена закону распределения с плотностью Найти коэффициент а, функцию распределения F(x) и P{X  3}, P{2 < X < 5}, P{X > 3,5}.

9.9. Непрерывная случайная величина Х имеет функцию распределения Найти числовые характеристики M[X], D[X], [X] данной случайной величины.

9.10. Непрерывная случайная величина Х подчинена закону распределения с плотностью Найти коэффициент а, функцию распределения F(x) и P{2 < X < 4}, P{–2  X < 2}.

9.11. Скорость молекул газа имеет плотность вероятности (закон Максвелла) ( ). Найти математическое ожидание и дисперсию скорости молекул, а также величину A при заданном h. Указание: .

§10. Биномиальное распределение

Дискретная случайная величина Х называется биномиальной с параметрами n, p (n  N, 0 < p < 1), если её возможные значения 0, 1, 2, …, n, а их вероятности определяются по формуле Бернулли , где .

Математическое ожидание и дисперсия биноминальной случайной величины выражается через её параметры следующим образом:

; .

10.1. Случайная величина X распределена биномиально с параметрами n = 4, p = 0,5. Найти Р{0,5  X  2,5}.

10.2. Вероятность выигрыша в лотерею по одному лотерейному билету равна 0,05. Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадают выигрыши, если приобретено 40 билетов.

10.3. В партии 90% стандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырёх отобранных.

10.4. Найти дисперсию дискретной случайной величины Х – числа появления события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M[X] = 0,9.

10.5. Завод изготавливает 80% изделий первого сорта и 20% второго. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа изделий первого сорта в партии из 1000 отобранных случайным образом изделий.

10.6. Найти постоянную вероятность попадания в цель при каждом выстреле и число произведённых выстрелов, если среднее число попаданий равно 72, а среднее квадратическое отклонение случайной величины, характеризующей число попаданий, равно 6.

10.7. Два игральных кубика одновременно бросают два раза. Написать закон распределения случайной величины Х – числа выпадения чётного числа очков на двух игральных кубиках.

10.8. Вероятность того, что лампа остается исправной после 1000 часов работы, равна 0,2. Написать закон распределения случайной величины Х – числа неисправных ламп после 1000 часов работы из трех имеющихся. Найти числовые характеристики данной случайной величины.