4.2. Доверительные интервалы
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, и часто для исследований более эффективны интервальные оценки.
О. 1. Интервальной называют оценку, которая определяется некоторым промежутком (интервалом). Такие оценки позволяют установить точность и надежность выборочных оценок.
Очевидно,
статистическая оценка
тем точнее, чем меньше абсолютная
величина разности
,
т. е.
(*), где
есть погрешность.
О. 2. Вероятность γ, с которой можно утверждать, что выполняется неравенство (*), называется надежностью или доверительной вероятностью.
На практике надежность обычно задают близкой к единице, т. е. берут γ = 0,95, γ = 0,99, γ = 0,999.
Итак,
или
есть вероятность того, что интервал
заключает в себе неизвестный параметр
.
О. 3. Интервал , который содержит неизвестный параметр с заданной надежностью γ, называется доверительным интервалом (рис. 14).
О. 4.
Числа
называются доверительными границами.
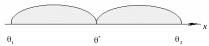
δ δ
Рис. 14. Доверительный интервал
Чем меньше δ, тем выше точность оценки.
О. 5.
называется уровнем значимости.
При
увеличении объема выборки длина
доверительного интервала уменьшается,
а с приближением
длина его увеличивается.
4.3. Доверительные интервалы для параметров нормального распределения Доверительный интервал для математического ожидания при известном σ
Пусть для некоторой случайной величины, распределенной по нормальному закону, известно среднее квадратическое отклонение, а сами значения этой с.в. получены в эксперименте (имеется выборка). Требуется определить среднее значение данной с.в., учитывая известное σ. Задача оценки истинного значения измеряемой величины формулируется как задача оценки математического ожидания или центра нормального распределения. Выбрав надежность γ, строим доверительный интервал для математического ожидания:
.
Здесь
значение параметра t
находим из условия
,
где Ф(t) есть
затабулированная интегральная функция
Лапласа
(см. табл. П. 1).
О. 1.
Оценка
называется классической.
Погрешность
определяет точность классической
оценки.
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном σ
Пусть с.в. Х генеральной совокупности распределена нормально, но теперь среднее квадратическое отклонение (СКО) σ неизвестно.
Тогда доверительный интервал для математического ожидания
,
где
– выборочная средняя;
– исправленное среднее квадратическое
отклонение; n
– объем выборки;
находим по таблице квантилей
распределения Стьюдента (см. табл. П.
2).
Доверительный интервал для ско нормального распределения
Пусть с.в. Х распределена нормально. Требуется оценить СКО σ генеральной совокупности по исправленному выборочному СКО.
Тогда доверительный интервал для СКО
,
при q < 1;
,
при q > 1,
где
определяется по табл. П. 3.
4.4. Решение типовых задач
Пример 1. Из ГС извлечена выборка объема n = 50.
-
хi
2
5
7
10
ni
16
12
8
14
Найти несмещенную оценку генеральной средней, оценку генеральной дисперсии и исправленную оценку генеральной дисперсии.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя, т. е.
.
Оценкой генеральной дисперсии является выборочная дисперсия
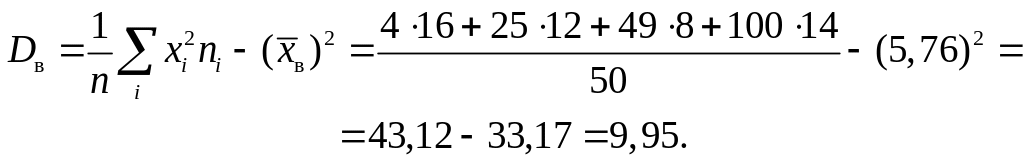
Соответственно, исправленной оценкой генеральной дисперсии является величина
.
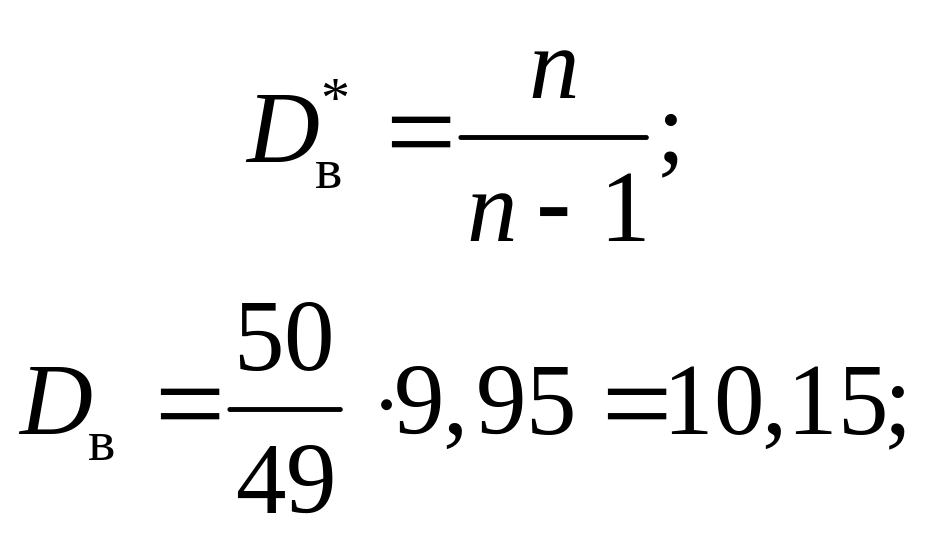
Пример 2. Найти точечные оценки для выборки
-
хi
186
192
194
ni
2
5
3
Решение. Перейдем к новым переменным. Пусть c = 192 – «ложный нуль».
-
ui
– 6
0
2
ni
2
5
3
Вычислим выборочное среднее:
.
Пример 3. Автомат режет проволоку, проектная длина которой 5 см, а среднее квадратическое отклонение 0,3 см. Контролер производил выборочные измерения и получил следующие результаты: 51, 47, 48, 46, 54, 49, 47, 50, 53, 46, 46, 47, 48, 49, 52, 51, 48, 47, 49, 51, 45 (в мм). Учитывая, что длина отрезка – величина, распределенная по нормальному закону, найдите с надежностью 0,95 доверительный интервал для математического ожидания генеральной совокупности (нарезанной проволоки) и примите решение о необходимости доналадки автомата.
Решение. Построим сгруппированный вариационный ряд.
хi |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
ni |
1 |
3 |
4 |
3 |
3 |
1 |
3 |
2 |
1 |
Объем выборки n = 21. Найдем выборочное среднее хв = 48,76. Среднее квадратическое отклонение известно: = 3 мм. Из условия 2Ф(t) = 0,95 по таблице найдем t = 1,96. Тогда точность вычислим по формуле . Получаем = 1,28.
Строим доверительный интервал для математического ожидания с известным = 3 мм:
48,76 – 1,28 < a < 48,76 + 1,28,
47,48 < а < 50,04.
Вообще говоря, в допустимые размеры от 47 мм до 53 мм данные выборки попадают, но, очевидно, следует отрегулировать автомат для большей точности.
Пример 4. Фирма «Бублик» заявляет, что вес их изделий равен 100 г. Петя решил проверить правдивость фирмы. Сколько бубликов ему нужно купить, чтобы с вероятностью 0,99 убедиться в том, что истинный вес отклоняется от рекламируемого не более чем на 3 г? Учтите, что у Пети есть весы, систематическая ошибка взвешивания на которых равна нулю, а случайные ошибки подчинены нормальному закону со средним квадратическим отклонением 5 г.
Решение. Исследуемое
отклонение истинного веса от рекламируемого
3 г – это точность .
Значение t находим по
таблице из условия 2Ф(t)
= 0,99. Получаем t = 2,54.
Из формулы
находим
,
то есть Пете нужно купить не менее 18
бубликов, чтобы определить истинный
вес бубликов этой фирмы.
Пример 5. В пруду выращивается рыба. Когда рыба достигнет своего промышленного веса 750 г, можно объявлять массовый лов. Технолог рыбозавода произвел контрольное взвешивание и получил следующие результаты: 680, 695, 780, 657, 723, 745, 790, 715, 735, 689, 693, 727, 685, 758, 762, 742, 794, 652, 673, 763, 683, 789, 770, 670, 648, 784, 791, 621, 753, 698, 768, 675, 729, 762, 772, 657, 683, 758, 795, 760. Построив доверительный интервал, с надежностью 0,95 определите, следует ли разрешать массовый лов.
Решение. Так как величины достаточно плотно расположены на числовой шкале, построим интервальный ряд из 5 интервалов. Объем выборки – 40. Наименьшее значение – 621, наибольшее – 795. Размах выборки – 174. Длина интервала 174 : 4 = 43,5, левая граница интервального ряда – 599,25.
хi; хi+1 |
599,25; 642,75 |
642,75; 686,25 |
686,25; 729,75 |
729,75; 773,25 |
773,25; 816,75 |
ni |
1 |
11 |
9 |
13 |
6 |
|
621 |
664,5 |
708 |
751,5 |
795 |
Используя данные интервального ряда, находим выборочное среднее хв = 721,05 и исправленное среднее квадратическое отклонение S = 49,1.
Учитывая надежность = 0,95 и объем выборки n = 40, находим t по таблице квантилей распределения Стьюдента: t = 2,023.
Строим доверительный интервал для математического ожидания нормально распределенной генеральной совокупности при неизвестном :
или 705,33 < а < 736,77.
Пока лов рыбы начинать рано.
Пример 6. Произведено: а) 12; б) 6 измерений расстояния новым дальномером. Исправленное СКО S случайных ошибок измерения оказалось равным 0,6 м. Найти точность прибора с надежностью 0,99.
Решение. Точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерения. А случайные ошибки любого измерения – нормально распределенная случайная величина. Поэтому необходимо найти доверительный интервал для СКО генеральной совокупности.
а) γ = 0,99, n = 12, по табл. П. 3 находим q(0,99; 12) = 0,9 < 1.
Тогда доверительный интервал находим по формуле
0,6(1 – 0,9) < σ < 0,6(1 + 0,9).
Окончательно получаем 0,06 м < σ < 1,14 м. Это и есть точность испытываемого дальномера.
б) γ = 0,99, n = 6, по табл. П. 3 находим q(0,99; 6) = 2,01 > 1.
Тогда доверительный интервал находим по формуле
0 < σ < 0,6(1 + 2,01).
Окончательно получаем 0 < σ < 1,806 м. Это и есть точность испытываемого дальномера.
На этом примере можно убедиться, что большее количество испытаний дает более точную оценку.