7.3. Решение типовых задач

Пример 1.

У предпринимателя имеется 3 магазина. В каждом из них он проводит рекламу товара пятью способами и фиксирует доход (в тыс. руб.). Результаты сведены в таблицу.

При уровне значимости проверить гипотезу о значимости фактора рекламы.

Способ рекламы	F1	F2	F3
1	50	91	75
2	60	70	64
3	35	66	79
4	69	96	70
5	40	98	81

Для построения дисперсий необходимо найти выборочные средние по каждому уровню и выборочную среднюю по всему массиву.

Найдем значение выборочной средней по всему массиву по формуле

,

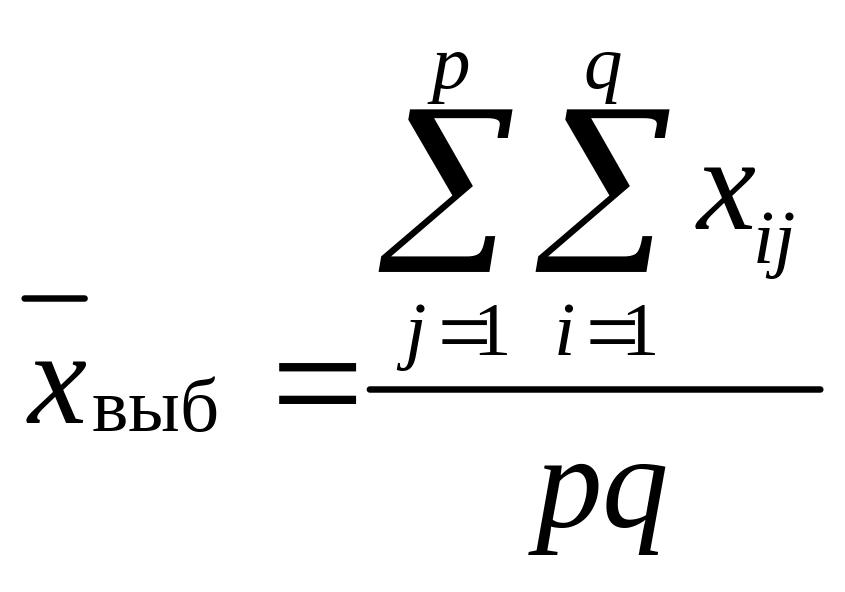где р – количество испытаний; q – количество уровней.

Результаты расчета групповых средних сведем в приведенную ниже таблицу:

Номер уровня	Суммы по каждому уровню
1	217
2	196
3	183
4	239
5	224
Всего	1059

Таким образом, .

Вычислим по формуле

.

Для этого оценим разность квадратов отклонений наблюдаемой величины и выборочной средней по всему массиву:

			Суммы по уровням
424,36	416,16	19,36	859,88
112,36	0,36	43,56	156,28
1267,36	21,16	70,56	1359,08
2,56	645,16	0,36	648,08
936,36	750,76	108,16	1795,28
Общая сумма			4818,6

Таким образом, суммируя числа в последнем столбце таблицы, получаем общую среднюю

.

Вычислим факторную сумму по формуле

,

где р – количество испытаний; q – количество уровней.

Предварительно найдем значения выборочных средних по каждому уровню по формуле

.

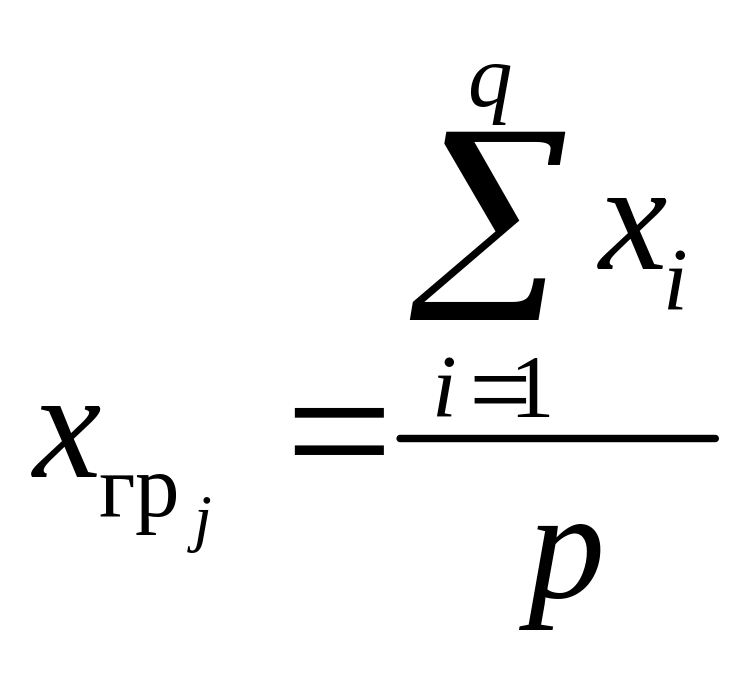Получаем .

Учитывая полученное ранее значение выборочной средней по всему массиву и выборочные средние по каждому уровню, приведем вычисления для расчета факторной суммы:

	1	2	3
	50,8	84,2	73,8
	– 19,8	13,6	3,2
	392,04	184,96	10,24
		Общая сумма

Получаем .

Таким образом, получаем .

Найдем остаточную сумму по формуле

.

Значения средних по каждому уровню были получены ранее:

i				Суммы по уровню
1	0,64	46,24	1,44	48,32
2	84,64	201,64	96,04	382,32
3	249,64	331,24	27,04	607,92
4	331,24	139,24	14,44	484,92
5	116,64	190,44	51,84	358,92

Складывая числа в последнем столбце таблицы, получаем .

Для контроля расчета остаточной суммы можно использовать основное тождество дисперсионного анализа: .

Таким образом,

.

Выдвигаем гипотезу H₀: групповые средние равны.

Конкурирующая гипотеза H₁: групповые средние не равны.

Для проверки гипотезы о влиянии фактора на величину рассмотрим случайную величину .

Для этого предварительно найдем несмещенные оценки дисперсий по формулам

, .

Получаем

; .

Таким образом, .

Сравним полученное значение с табличным значением , где , из табл. П. 6 при уровне значимости .

Получаем .

Так как , следовательно, утверждать равенство групповых средних нельзя, то есть гипотеза о влиянии фактора на случайную величину подтверждается.

Пример 2.

Три группы водителей обучались по различным методикам. После окончания срока обучения был произведен те­стовый контроль над случайно отобранными водителями из каж­дой группы. Получены следующие результаты:

i-я методика	Количество допущенных ошибок
	1 группа	2 группа	3 группа
1	1	2	4
2	3	3	5
3	2	2	3
4	1	1	–
5	0	4	–
6	2	–	–
7	1	–	–
	10	12	12

При уровне значимости проверить гипотезу об отсут­ствии влияния различных методик обучения на результаты тесто­вого контроля водителей. Предполагается, что выборки получены из независимых, нормально распределенных совокупностей с одной и той же дисперсией.

В нашем случае p = 3, n = 7 + 5 + 3 = 15.

Вычисления удобно проводить в такой последовательности.

Определяем общее количество ошибок

.

.

Для расчетов сумм квадратов используем формулы

;

;

.

Предварительно находим несмещенные оценки дисперсий

;

.

Вычисляем величину .

Находим величину при уровне значимости (учитывая, что ) (табл. П. 6).

Так как , то гипотеза о равенстве средних отклоняется: исследуемые методики обучения водителей дают значимо различ­ные результаты тестового контроля.

Линейные контрасты

Если гипотеза H₀ о равенстве средних отклоняется, то требуется определить, какие именно группы имеют значимое различие средних. Для этих целей ис­пользуется метод линейных контрастов. Линейный контраст Lk определяется как линейная комбинация:

,

где – константы, однозначно определяемые из формулировки проверяемых гипотез, причем ; – средние групповые.

Оценка равна , а оценка дисперсии равна

.

Границы доверительного интервала для имеют вид

. (2)

Пример 3. В условиях примера 1 при двусторонних альтернативных гипотезах проверить гипотезы

,

,

,

.

В соответствии с проверяемыми гипотезами , , определяем линейные контрасты

; , , ;

; , , ;

; , , ;

; , ; .

Найдем границы доверительных интервалов для линейных конт­растов , .

Предварительно вычислим оценки линейных контрастов и их дисперсий. Выборочные средние

, , .

Оценка дисперсии

.

Оценки контрастов и их дисперсий

, ;

, ;

, ;

;

.

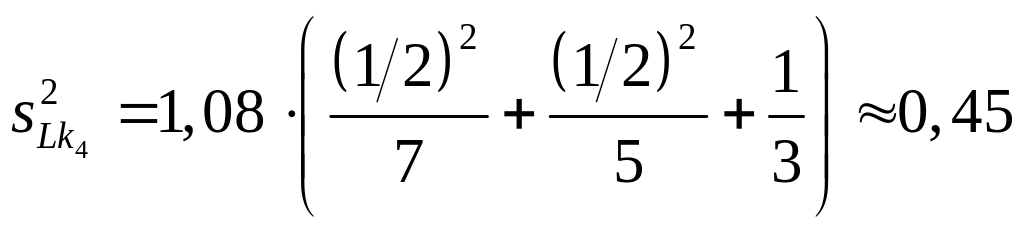При уровне значимости по табл. П. 6 находим . Чтобы определить доверительные интервалы для линейных контрастов, предварительно вычислим

.

Таким образом, доверительные границы для контрастов , , по формуле (2) равны соответственно ; ; ; .

Так как нулевое значение накрывается доверительными интервалами для и , то гипотезы и принимаются, гипотезы и отклоня­ются.

Таким образом, значимо различны средние первой и третьей группы, а также среднее арифметическое средних для первых двух групп и среднее третьей группы.