2. Способы сбора информации

Пусть требуется изучить некоторую совокупность однородных объектов относительно качественных и количественных признаков. Например, для партии деталей

• качественный признак Х – стандартность детали;

• количественный признак Х – контролируемый размер детали.

Различают следующие способы сбора информации:

Сплошное обследование всех единиц изучаемой совокупности.

Н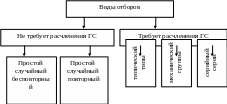 есплошное обследование, т. е. случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению (рис. 2).

Рис. 2. Виды отборов

О. 1. Генеральная совокупность (ГС) – это все объекты, предназначенные для исследования.

О. 2. Количество объектов (элементов) ГС называется ее объемом (N).

На практике в случае большого объема ГС сплошное исследование физически невозможно, а также связано с большими трудовыми и материальными затратами.

О. 3. Выборочной совокупностью (ВС) или просто выборкой называют все случайно отобранные из генеральной совокупности объекты, предназначенные для непосредственного исследования.

О. 4. Число элементов в выборке называется объемом выборки (n).

О. 5. Выборка, правильно представляющая пропорции ГС, называется репрезентативной (т. е. объективно отражающая ГС).

Для репрезентативной выборки следует придерживаться принципов случайности и достаточности числа взятых объектов.

3. Первичная обработка выборки

Пусть из ГС извлекли выборку, причем разные объекты имеют разные числовые значения (x_i) изучаемого параметра.

О. 1. Наблюдаемые значения изучаемого параметра (количественного либо качественного признака) называются вариантами (x_i).

О. 2. Последовательность вариант, записанная в порядке возрастания (убывания), называется вариационным рядом.

есть вариационный ряд,

если (или х₁ ≥ х₂ ≥ х₃ ≥ … ≥ х_n).

О. 3. Число, показывающее, сколько раз данная варианта x_i встречается в совокупности, называется частотой варианты (n_i).

Очевидно, что для любой выборки .

О. 4. Отношение называется относительной частотой варианты ( , т. к. ).

О. 5. Статистическим распределением выборки (или статистическим рядом) называется перечень вариант x_i вариационного ряда и соответствующих им частот n_i (либо относительных частот ω_i).

xi	x1	x2	…	xk	либо	xi	x1	x2	…	xk
ni	n1	n2	…	nk		i	1	2	…	k

При большом объеме выборки или при незначительных отклонениях вариант строят интервальный статистический ряд: интервал, содержащий все значения выборки, разбивают на k равных интервалов и подсчитывают частоты интервалов.

О. 6. Размахом выборки называют расстояние между наименьшим и наибольшим значением вариант этой выборки.

Расчет длины и границ интервалов проводится по следующим формулам:

,

где k – количество задаваемых интервалов;

= х₁; ;

остальные границы рассчитываются по формуле x_i = x_i–1 + ∆x.

О. 7. Частотой интервала называется количество всех вариант, попавших в данный интервал.

Интервальный статистический ряд имеет вид

№	(xi, xi+1)	ni
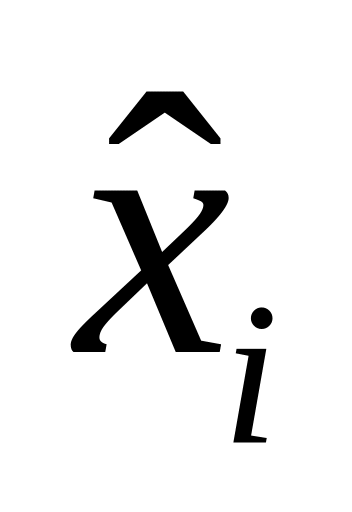
1	(x1, x2)	n1
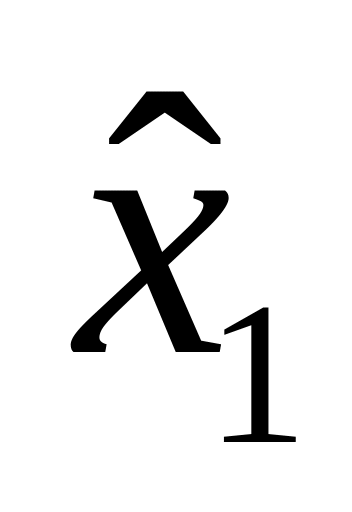
2	(x2, x3)	n2
…	…	…	…
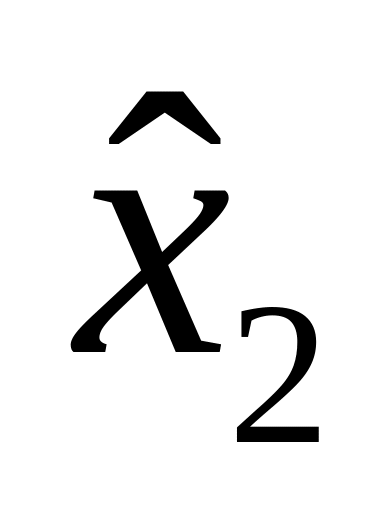
k	(xk–1, xk)	nk

____________

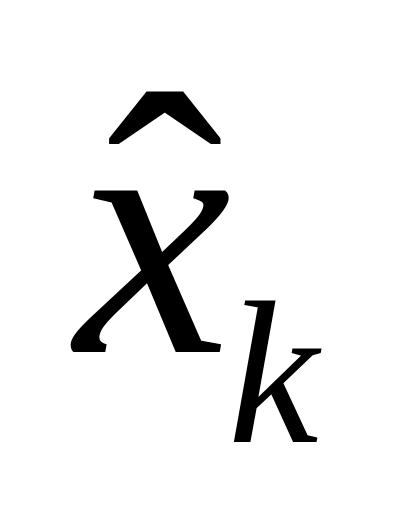
– середина интервала (x_i, x_i+1).

Геометрической интерпретацией статистического ряда являются полигон и гистограмма частот.

О. 8. Полигоном частот называют ломаную на координатной плоскости, отрезки которой соединяют последовательно точки (x₁, n₁), (x₂, n₂), …, (x_k, n_k) (рис. 3).

О. 9. Полигоном относительных частот называют ломаную на координатной плоскости, отрезки которой последовательно соединяют точки (x₁, ω₁), (x₂, ω₂), …, (x_k, ω_k) (рис. 4).

n_i

n_k

n₂

n₁

x₁ x₂ x₃ x_k x_i

Рис. 3. Полигон частот

ω_i

ω₂

ω₁

x₁ x₂ x₃ x_k x_i

Рис. 4. Полигон относительных частот

Если статистический ряд интервальный, то для него строят гистограмму частот (либо относительных частот).

О. 10. Гистограммой частот (рис. 5) называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы (x_i, x_i+1) длиной Δх, а высоты равны отношению

.

Площадь i-го прямоугольника равна сумме частот вариант, попавших в i-й интервал:

.

Тогда площадь всей гистограммы частот равна сумме всех частот, т. е. объему выборки n:

.

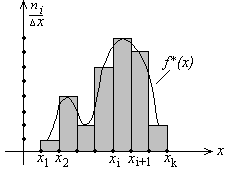
Рис. 5. Гистограмма частот

На гистограмме частот строят эмпирическую функцию плотности распределения f ^*(x).

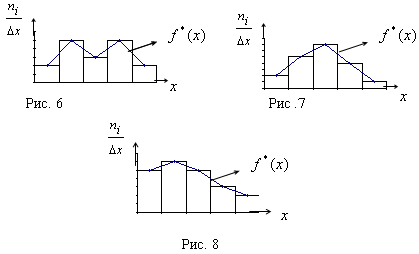
По виду f^*(x) можно выдвинуть гипотезу о виде распределения изучаемого признака, который можно рассматривать как случайную величину Х (с.в. Х). Например, можно предположить, что на рис. 6 признак Х распределен равномерно, на рис. 7 – нормально, на рис. 8 – по показательному закону.

Аналогично строят гистограмму относительных частот (рис. 9).

x₁ x₂ x₃ x_k–1 x_k x_i

Рис. 9. Гистограмма относительных частот

Площадь гистограммы определяется по формуле

.

На основании статистического ряда строится эмпирическая (полученная опытным путем) функция распределения.

О. 11. Эмпирической функцией распределения (обозначается F^*(x)) называют функцию, определяющую для каждого числа x относительную частоту события X < x:

,

где n_x – число вариант, меньших х; n – объем выборки.